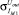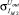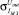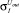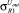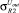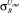Стабилизатор напряжения с низким падением напряжения на регулирующем элементе может применяться в самых разнообразных устройствах, таких как сетевые платы, системы беспроводной связи, декодеры кабельного телевидения, медицинское и промышленное оборудование, ноутбуки и т.д.
Основными источниками погрешностей стабилизатора напряжения являются следующие его блоки: источник опорного напряжения (ИОН), регулирующий элемент, усилитель ошибки, резистивный делитель. При этом именно ИОН в основном определяет точность выходного напряжения стабилизатора.
Отклонения значений параметров элементов интегральных схем от номинальной величины являются следствием пространственных и временных флуктуаций технологического процесса. При этом целесообразно разделить разброс параметров элементов в пределах одного кристалла (локальный разброс или рассогласование параметров) с одной стороны и между элементами, расположенными на разных кристаллах (глобальный разброс или групповые отклонения) – с другой. В связи с тем, что разброс характеристик элементов носит случайный характер, для оценки его влияния на точность функционального блока следует использовать статистический подход [3]. Он позволяет решить следующие задачи:
- получить максимальный процент выхода годных кристаллов (снизить долю параметрического брака) путем оптимального выбора размеров элементов и их взаимного расположения, а также электрической схемы, малочувствительной к разбросу параметров элементов;
- достичь максимальной параметрической надежности проектируемых ИС;
- снизить риски неоптимального проектирования.
Основным инструментом статистического анализа электронных схем является численный метод Монте-Карло. Он определяет статистику выходных параметров с высокой степенью достоверности при различных распределениях параметров отдельных элементов. Однако, как и большинство численных методов, он обладает двумя существенными недостатками: наряду с немалыми требованиями к вычислительным ресурсам, он не дает сведений о тенденциях в поведении характеристик схемы при изменении исходных номинальных значений ее элементов. В связи с этим возрастает интерес к аналитическим подходам, в том числе основанным на понятии чувствительности схемы к малым отклонениям номиналов.
Используя аппарат чувствительности, оценим точность основного блока стабилизатора напряжения – источник опорного напряжения. Типичная схема ИОН в КМОП-исполнении приведена на рис. 1. В его состав входят резисторы R1, R2, биполярные транзисторы Q1-Q3, МОП транзисторы М1-М3 и операционный усилитель A1. Предполагаем, что статистические характеристики параметров элементов заданы.
Отклонение опорного напряжения ΔUout от номинального значения Uout равно сумме величин группового отклонения технологического процесса (ΔU out,proc) и разброса рассогласования элементов (∆U out,mism) [5]:
∆Uout = ∆U out,proc + ∆U out,mism, (1)
причем
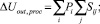
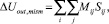
где Pi – групповое отклонение элементов i-й группы; Мij – отклонение рассогласования j-го элемента i-й группы; Sij – чувствительность j-го элемента, принадлежащего i-й группе.
Тогда дисперсия опорного напряжения может быть выражена так:
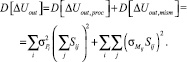 (2)
(2)
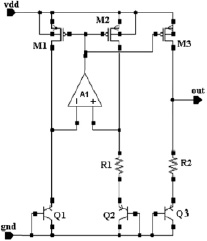
Рис. 1. Схема источника опорного напряжения
Среднеквадратическое отклонение Uout соответственно равно:
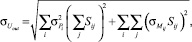 (3)
(3)
где 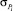 – среднеквадратическое отклонение элементов i-й группы при учете отклонения технологического процесса;
– среднеквадратическое отклонение элементов i-й группы при учете отклонения технологического процесса; 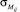 – среднеквадратическое отклонение j-го элемента i-й группы при учете рассогласования элементов.
– среднеквадратическое отклонение j-го элемента i-й группы при учете рассогласования элементов.
В статье рассматривается только влияние рассогласования элементов, а именно МОП-транзисторов и резисторов, на выходное напряжение ИОН.
В числе основных данных, описывающих статистические характеристики элементов, обычно доступны стандартные отклонения номиналов резисторов и токов стока МОП-транзисторов при заданных значениях напряжения затвор-исток. Через эти характеристики и следует выразить выходное напряжение источника. Это напряжение, очевидно, равно:
Uout = IM3R2 + UБЭ3. (4)
Для контура, включающего входы операционного усилителя A1, резистор R1 и биполярные транзисторы Q1, Q2, справедливо соотношение
(IM2R1 + UБЭ2) – (UБЭ1) = 0. (5)
Используя зависимость тока эмиттера биполярного транзистора от напряжения база-эмиттер:
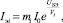 (6)
(6)
где Vt = k·T/q – тепловой потенциал; I0 – тепловой ток биполярного транзистора; mi – характеризует количество параллельно включенных биполярных транзисторов с заданной площадью эмиттера.
Пусть для биполярного транзистора Q1 m1 = 1, а для Q2 m2 = m. Учитывая, что IMi = Iэi.
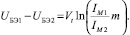 (7)
(7)
Тогда на основе (5, 7) для тока стока транзистора M2 можно получить
 (8)
(8)
если ток IM3 представить следующим образом:
 (9)
(9)
то напряжение база-эмиттер биполярного транзистора Q3 будет равно
 (10)
(10)
В этих условиях, подставим (9), (10) в (4), выходное напряжение приобретает следующий вид:
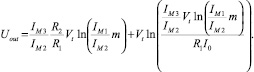 (11)
(11)
Полуотносительные чувствительности к токам [1]:
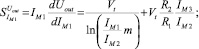 (12а)
(12а)
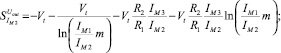 (12б)
(12б)
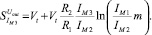 (12в)
(12в)
И к резисторам:
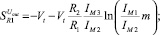 (13а)
(13а)
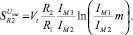 (13б)
(13б)
Полученные выражения следует рассматривать при определенном соотношении между резисторами, обеспечивающем формирование «купола» [2, 3] выходного напряжения в нужном диапазоне температур. Оно задается условием экстремума
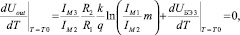
откуда
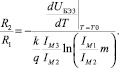 (14)
(14)
С учетом этого условия (14) выражения для чувствительностей (12), (13) принимают следующий вид:
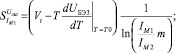 (15а)
(15а)
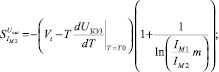 (15б)
(15б)
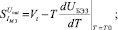 (15в)
(15в)
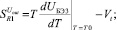 (16а)
(16а)
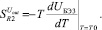 (16б)
(16б)
Используя выражения (15), (16), рассчитаем отклонение выходного напряжения ИОН, вносимое рассогласованием токов МОП-транзисторов М1-М3 и номиналов резисторов R1, R2.
Известно, что среднеквадратическое отклонение тока интегральных МОП-транзисторов задается следующим выражением:
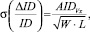
где W, L – ширина и длина канала МОП транзистора соответственно; Vx = VGS – VTH – разность затвор-исток и порогового напряжений МОП транзистора; AIDVx – среднеквадратическое отклонение тока на единицу площади затвора.
Значение AIDVx зависит от разности напряжения затвор-исток и порогового напряжения МОП-транзистора. Типичное значение AIDVx при Vx = 0,2 В для рассматриваемой схемы составляет 5,68·10–6 (%∙мкм).
В табл. 1 приведены результаты расчета стандартного отклонения выходного напряжения для раздельного и суммарного влияния рассогласований токов в соответствии с (3) вместе с результатами моделирования методом статистических испытаний в среде Cadence.
Таблица 1
Среднеквадратическое отклонение выходного напряжения, вносимое отклонением тока МОП-транзисторов
|
Параметр |
Расчет |
Моделирование |
|
|
1,32 мВ |
1,31 мВ |
|
|
4,06 мВ |
4,00 мВ |
|
|
2,74 мВ |
2,67 мВ |
|
|
5,07 мВ |
5,03 мВ |
Гистограмма значений выходного напряжения для этого случая приведена на рис. 2.
Среднеквадратическое отклонение номиналов резисторов задается следующим выражением:
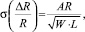
где W, L – ширина и длина резистора соответственно; AR – среднеквадратическое отклонение номинала резистора на единицу площади.
В реальном проекте ИОН резистор R1 имел параметры W = 2 мкм, L = 30 мкм, и R2 c параметрами W = 2 мкм, L = 250 мкм, при величине AR = 1,2·10–8 мкм. Рассчитанные значения среднеквадратического отклонения сведены в табл. 2, там же отображены результаты моделирования Монте-Карло. Гистограмма значений выходного напряжения для этого случая приведена на рис. 3.
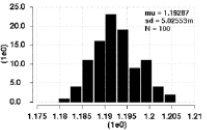
Рис. 2. Гистограмма, иллюстрирующая разброс выходного напряжения ИОН при рассогласовании МОП-транзисторов
Таблица 2
Среднеквадратическое отклонение выходного напряжения, вносимое отклонением номиналов резисторов
|
Параметр |
Расчет |
Моделирование |
|
|
0,744 мВ |
0,765 мВ |
|
|
0,244 мВ |
0,242 мВ |
|
|
0,783 мВ |
0,801 мВ |
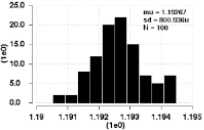
Рис. 3. Гистограмма, иллюстрирующая разброс выходного напряжения ИОН при рассогласовании резисторов (при построении использован метод Monte-Carlo).
Проведенный анализ схемы ИОН с использованием аппарата чувствительности приводит к следующим выводам:
- как следует из (15), (16) одним из основных факторов, вносящих вклад в величину разброса опорного напряжения, является величина температурного коэффициента напряжения база-эмиттер биполярных транзисторов;
- уменьшить влияние рассогласования токов МОП-транзисторов (M1-M3) на выходное напряжение ИОН можно двумя путями: увеличением коэффициента m (отношение площадей эмиттеров биполярных транзисторов SQ2/SQ1), либо увеличением отношения токов IM1/IM2;
- сравнение расчетных значений с результатами моделирования методом Монте-Карло показало высокую точность оценки отклонения, полученное с использованием аппарата чувствительности.
Рецензенты:
Петров Б.К., д.т.н., профессор кафедры физики полупроводников и микроэлектроники Воронежского государственного университета, г. Воронеж;
Строгонов А.В., д.т.н., профессор кафедры полупроводниковой электроники и наноэлектроники Воронежского государственного технического университета, г. Воронеж.
Работа поступила в редакцию 26.03.2014.