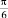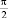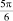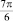Миссия Национального исследовательского Томского политехнического университета заключается в повышении конкурентоспособности страны и создании ресурсоэффективных технологий [4]. Все это должно обеспечиваться за счет интернационализации и интеграции исследований, образования и практики подготовки инженерной элиты.
Подготовка инженерной элиты начинается с первых курсов. В рабочих программах курса «Математика» и естественнонаучных дисциплин, которые изучаются на младших курсах, отмечается, что в процессе освоения курса у студентов должны развиваться универсальные и профессиональные компетенции, повышаться их творческий потенциал.
В последнее время акцент в организации учебного процесса смещается в сторону усиления роли самостоятельной работы студентов. В настоящее время многие исследования посвящены разработке форм, способов, средств и содержания организации внеаудиторной самостоятельной работы студентов технических вузов, с помощью которых можно обеспечить компетентностный подход при изучении курса «Математика» и других дисциплин.
Самостоятельную работу, как правило, разделяют на аудиторную и внеаудиторную. Н.В. Фомин [5], кроме аудиторной и внеаудиторной самостоятельной работы, выделяет инициативную самостоятельную работу, которая не предусматривается основной образовательной программой и осуществляется студентами по собственной инициативе с целью реализации своих учебных и научных интересов (участие в научных исследованиях, в выполнении проектно-конструкторских работ и т.д.).
По нашему мнению, на младших курсах необходимо сначала развивать творческую составляющую внеаудиторной самостоятельной работы, потому что основная часть студентов на первом и втором курсах не способна осуществить самостоятельную работу по собственной инициативе.
Наши исследования [1] показали, что организация самостоятельной работы по курсу математики должна быть ориентирована на развитие у студентов:
- умений интегрировать полученные теоретические знания по математике для решения познавательных и творческих задач;
- умений научно-исследовательского характера;
- способностей демонстрировать базовые знания в области математики;
- способностей эффективно работать как в качестве члена команды, так и индивидуально.
Одним из основных направлений модернизации образовательной деятельности ТПУ [6] является модернизация учебного процесса в университете в условиях личностно-ориентированной среды, что предусматривает:
1) сокращение лекционной составляющей аудиторной работы студентов до 20–40 % и увеличение доли практических и интерактивных форм организации учебного процесса до 30–40 % (технологии проблемного, проектного, контекстного обучения, case-study, мастер-классы и др.);
2) введение в график учебного процесса конференц-недель, предназначенных для предоставления студентам возможности продемонстрировать результаты своей самостоятельной работы.
В Томском политехническом университете в каждом семестре на протяжении трёх лет проводятся две конференц-недели. В рамках конференц-недели преподаватель может планировать такие виды работ, как контрольные работы, коллоквиумы, защита отчета по лабораторной работе, защита индивидуального домашнего задания, круглый стол, выступление с докладом и т.д.
Одной из творческих форм организации самостоятельной работы, по нашему мнению, могут быть образовательные интегративные проекты по математике и информатике.
В зависимости от раздела математики, интегративные образовательные проекты мы разделили на базовые, наглядно-иллюстративные и на интегративные проекты вычислительного характера.
При выполнении интегративного проекта студенту необходимо провести теоретическое исследование и найти практическое решение проблемы. Визуальную картину решения проблемы студенты должны продемонстрировать на экране компьютера.
Работа над интегративным проектом предполагает использование прикладных программных средств компьютера, в нашем случае СКМ Mathcad и табличного редактора Microsof Ехсе1, которые дают возможность создавать схемы, графики функций, таблицы и т.д.
Работу над интегративными проектами обучающиеся выстраивают в виде проектной деятельности, когда они самостоятельно добывают знания, пользуясь при этом не только классическими учебниками по математике, но и информацией, которая размещена на образовательных web-сайтах справочного характера и консультативного назначения. На сайтах обучающиеся могут найти не только теоретический материал, связанный с проектами, но и подробную информацию по работе с табличным процессором Microsoft Excel, по работе со средством создания презентаций Microsoft PowerPoint, а также графические возможности текстового редактора Microsoft Word (рисование в документе Microsoft Word, диаграммы Microsoft Word, редактор формул Microsoft Equation).
Интегративные проекты по математике и информатике, поддерживающие учебный курс математики, мы обозначили как вводные интегративные проекты [2, 3]. Они связаны с ознакомлением и введением основных понятий темы (или раздела) курса.
Приведем один из примеров вводного интегративного проекта наглядно-иллюстративного характера. Проект «Как построить график в полярной системе координат».
Данный проект связан с построением графиков в полярной системе координат. При изучении темы «Вычисление площадей плоских фигур в полярной системе координат» очень важно уметь строить графики кривых, заданных в полярных координатах уравнением r = r(φ), где α ≤ φ ≤ β.
С учетом того, что на данную тему отводится 2 часа аудиторных занятий, а в индивидуальном задании и в контрольной работе обязательное включение задания на данную тему, студенту необходимо построить большое количество кривых, заданных в полярных координатах (более 20 различных кривых).
Приведем кривые, которые студенту необходимо научиться строить, чтобы освоить данную тему: окружности; области, заключенные между двумя окружностями; кривые семейства роз; кардиоиды; спираль Архимеда; лемнискату Бернулли; улитку Паскаля и др.
Построение графика кривой, заданной в полярных координатах, вручную довольно сложная задача. Сначала надо составить таблицу, задавая f (с маленьким шагом) и вычисляя значение r. Затем надо аккуратно строить лучи, проходящие через начало координат под углом f к оси Oх, и откладывать на них длины радиус-векторов. Раньше графики таких кривых строили на миллиметровке. Здесь очень важны точные вычисления и построение. Рассмотрим построение такого графика на бумаге.
Построим в полярной системе координат кривую r = 3∙(1 – sinφ).
Чтобы построить кривую, составим таблицу значений (шаг таблицы выбираем произвольно):
|
φ |
0 |
|
|
|
π |
|
|
2π |
|
r |
3 |
|
0 |
|
3 |
|
6 |
3 |
Строим точки в полярной системе координат, затем соединяем их плавной линией. Полученная кривая называется кардиоидой (рис. 1).
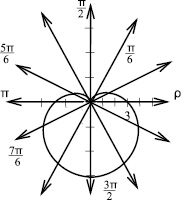
Рис. 1. Кардиоида, где ρ – полярная ось
В таблице приведено 8 значений f и r. Как правило, если обучающийся не знает, как выглядит кривая, ему необходимо будет составить таблицу, содержащую намного больше значений f и r. Такие вычисления требуют от студента большого количества времени.
Теперь рассмотрим построение такого графика с помощью программного пакета Mathcad. Сначала вводим на поле функцию r(φ) := 3∙(1 – sinφ). Затем, чтобы с помощью программного пакета Mathcad посчитать значения f и r, вводим на поле формулы:
N := 720, i := 0...N,
φi := 0 + 0,5∙i, ri := r(φi).
Нажимаем φi = и ri = . На поле выводится таблица значений f и r (рис. 2):
Значений f и r – 720. На экране все значения не видны, их можно посмотреть, щелкнув по таблице и установив полосу прокрутки. Изменяя значение N и в формуле φi := 0 + 0,5∙i множитель при i, автоматически высчитываются новые значения f и r. Отметим, что вычисляя 720 значений f и r даже с помощью калькулятора, обучающемуся понадобится намного больше времени. На экране компьютера вычисления происходят мгновенно.
Рис. 2. Таблица значений f и r, где f – полярный угол, r – полярный радиус точки
Последний этап – построение графика функции в полярной системе координат. В программном пакете Mathcad есть встроенная функция – график, двойным щелчком на поле вводим шаблон графика в полярной системе координат. Затем вводим f в место ввода внизу и слева – функцию r(f). Далее форматируем график, введя линии сетки. На экране получаем график кардиоиды (рис. 3).
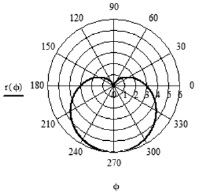
Рис. 3. Кардиоида, где Φ – полярный угол, r(Φ) – функция, заданная в полярных координатах
На экране можно проследить, как последовательно строится график на бумаге. Для этого надо ввести функцию и границы изменения f, например,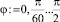 
. На экране появится часть графика, расположенного в первой четверти.
Таким образом, в учебном процессе нами совместно используются две технологии: изучение учебной темы на базе компьютера и с помощью компьютера.
Рассмотрим, что дает студенту работа над интегративным проектом «Как построить график в полярной системе координат».
Во-первых, у студентов формируются умения самостоятельной работы со специальной литературой, с информацией, которая содержится на сайтах справочного характера и консультативного назначения. На первоначальном этапе работы над интегративным проектом студент изучает классические учебники по математике, в которых содержится информация о полярной системе координат, о построении кривых в полярной системе координат. Там же студент может увидеть, как выглядят графики кривых в полярной системе координат. Данную информацию студент может также найти на сайтах справочного характера, на которых содержатся различные электронные энциклопедии, базы данных и литература по математике и информатике. Как правило, в таких источниках приводится небольшое количество примеров построения кривых, заданных в полярной системе координат. Как было отмечено выше, студенту в короткий срок необходимо построить более 20 кривых. Поэтому на втором этапе студент находит информацию по построению кривых (например, с помощью программного пакета Mathcad) в учебниках или на сайтах консультативного назначения. Сайты консультативного назначения предназначены для преподавателей и обучающихся по общеобразовательным предметам. В нашем случае студент ищет информацию, как работать с программным пакетом Mathcad и как использовать его для построения графиков в полярной системе координат.
Во-вторых, при работе над интегративным проектом у студентов развивается наглядно-образное мышление, имеющее важное значение в любом творческом процессе. Отметим, что программный пакет Mathcad позволяет проводить точное построение графиков, непрерывно менять графики, растягивать их, менять их цвет, строить несколько графиков в одной системе координат и т.д. Также на графике видны границы изменения полярного угла f. В дальнейшем эта информация необходима будет студенту при вычислении площадей кривых, заданных в полярных координатах в темах «Определенный интеграл» и «Двойной интеграл». Информацию по оформлению проекта обучающиеся могут найти на сайте http://www.metod-kopilka.ru.
В-третьих, работа над интегративным проектом по математике и информатике направлена на формирование у студента способностей эффективно работать как в качестве члена команды, так и индивидуально. Над интегративным проектом может работать как группа студентов, так и один студент. Количество участников проекта зависит от сложности проекта, от его продолжительности. Работая индивидуально над проектом, студент развивает такие качества личности, как выбор собственной стратегии, самостоятельность в принятии решений. Работая в команде, студент учится выслушивать чужое мнение, высказывать свои суждения, предлагать свое решение проблемы, отстаивать свою позицию. Именно наличие таких качеств необходимо современному инженеру.
Таким образом, в ходе работы над интегративным проектом по математике и информатике реализуется одна из целей, которую мы ставили при организации самостоятельной работы: научить студентов самостоятельно приобретать новые знания, используя современные образовательные и информационные технологии.
В заключение отметим, что при такой организации учебного процесса в ходе самостоятельной работы у студентов появляется интерес к учебе, формируется мотивация к будущей профессиональной деятельности.
Рецензенты:
Далингер В.А., д.п.н., профессор, заведующий кафедрой «Теория и методика обучения математике», ФГБОУ ВПО «Омский государственный педагогический университет», г. Омск;
Раскина И.И., д.п.н., профессор, заведующий кафедрой «Прикладная математика и информатика», ФГБОУ ВПО «Омский государственный педагогический университет», г. Омск.
Работа поступила в редакцию 21.03.2014.