В механизмах различных машин находят применение детали с постоянной формой поперечного сечения в виде правильных многогранников. Встречаются также детали с постоянным сечением сложной формы. В основе таких сечений лежат сложные кривые. Вопросам реализации различных способов формообразования таких поверхностей посвящены работы множества российских и зарубежных ученых.
Интерес для исследования представляют способы формообразования многогранных наружных поверхностей с переменным по длине профилем поперечного сечения. Характерным примером деталей, содержащих такие поверхности, является концевая часть заготовок пружин, применяемых в системе рессорного подвешивания тележек железнодорожных вагонов.
Ранее были рассмотрены способы формообразования многогранных наружных поверхностей с переменным по длине профилем поперечного сечения, выявлены их недостатки [5] и предложен принципиально новый способ формообразования наружных гранных поверхностей с переменным по длине профилем поперечного сечения, характеризующийся высокой производительностью [8, 12]. Особенностью способа является применение планетарного механизма [1, 11] с целью придания сложной траектории перемещения вершине металлорежущего инструмента.
Металлорежущий инструмент – многолезвийные резцовые блоки, представляющие собой корпус, выполненный в виде цилиндра с пазами для крепления сменных ножей, на которых закреплены сменные режущие пластины [10]. Режущие пластины, совершая перемещения по траектории трохоиды при осевой подаче заготовки, производят формообразование четырехгранного профиля концевых участков вагонных пружин. Ножи, закрепленные на корпусе резцовых блоков под углом к оси заготовки [4], позволяют получать переменный профиль поперечного сечения.
Действующие в процессе резания угловые геометрические параметры режущей части инструмента, а также плоскости, в которых они измеряются, не совпадают с заданными в процессе обработки [2, 3]. Значения угловых кинематических параметров режущего клина инструмента связаны с движением инструмента относительно заготовки в каждой рассматриваемой точке режущей кромки. Они рассчитываются на основе значений параметров с учетом взаимного расположения векторов скоростей главного и вспомогательного движений, а также связанных с ними плоскостей и поверхностей.
Следует отметить, что существенное влияние на прочность инструмента оказывает передний угол γ. С увеличением переднего угла облегчаются условия резания, уменьшается деформация и повышается качество поверхности. Сильное увеличение переднего угла приводит к значительному ослаблению режущих кромок. При обработке твердых и хрупких металлов применяют резцы с малыми передними углами, а при строгании мягких и вязких сталей стараются использовать инструмент с относительно большими передними углами. Задний угол α служит для уменьшения трения между задней поверхностью резца и обрабатываемой деталью, что ведет к уменьшению нагрева инструмента и в результате к увеличению его стойкости [13].
Для назначения рациональных геометрических параметров инструмента при обработке инструментом с планетарным движением необходимо установить изменение величины переднего и заднего углов в процессе обработки.
Для упрощения расчета изменения кинематических переднего и заднего углов рассмотрим процесс формообразования гранных поверхностей с переменным профилем в некоторой точке формообразуемой поверхности, которой будет соответствовать расстояние d от центра инструмента до вершины режущей кромки.
Сложное движение металлорежущего инструмента состоит из двух простых движений – вращения вокруг своей оси и вращения относительно заготовки. Рассмотрим характерные точки, в которых будет находиться вершина режущего инструмента в некоторый момент времени. Положение вершины режущей кромки в любой момент времени определяет параметр t.
Примем начало траектории движения вершины инструмента в точке А (r + d; 0), где t = 0° (поз. 1), тогда положение точки, в которой кинематические углы равны геометрическим, соответствует точке В (0; r–d), где t = 90ͦ°(поз. 2). Следовательно, положение вершины режущей кромки инструмента в точке врезания соответствует параметру t = 45 ͦ (поз. 3). Таким образом, для определения изменения величины кинематических переднего и заднего углов инструмента необходимо определить разность углов поворота инструмента в точке В с координатами (0; r–d), при t = 90° и точке С с координатами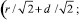 
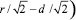, при t = 45°, соответствующей моменту врезания инструмента [7].
Параметрическое уравнение гипотрохоиды – траектории, описывающей перемещение вершины режущей кромки инструмента, имеет вид [1]:
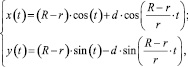(1)
где φ – параметр угла, изменяющийся от 0…2π; d – расстояние от центра вращения инструмента до его вершины; x, y – координаты точки гипотрохоиды на плоскости относительно центра координат О в системе координат XOY; R – радиус зубчатого колеса с внутренним зацеплением; r – радиус зубчатого колеса, на валу которого расположен инструмент.
Параметрические уравнения гипотрохоиды для соотношения R/r = 2 преобразуют к виду:
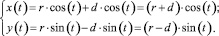(2)
Чтобы оценить величину изменения кинематического переднего и заднего углов необходимо определить координаты x(t0), y(t0) точки С гипотрохоиды, которой соответствует начало врезания инструмента.
Рассчитаем угол поворота φ0 как угол между лучами ОВ и ОС (рис. 1):
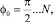(3)
где N – количество режущих ножей (для четырехгранного профиля N = 2).
Запишем уравнение тангенса угла φ:
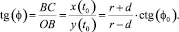(4)
С учетом, что N = 2, преобразуем формулу к следующему виду:
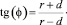(5)
Искомую величину ψтеор – изменение кинематического переднего угла инструмента определим следующим образом (рис. 1):
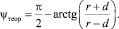(6)
Следует отметить, что величины изменения переднего и заднего кинематических углов описываются одной зависимостью, следовательно, изменение величины переднего угла соответствует изменению величины заднего кинематического угла.
В таблице представлен расчет изменения кинематических углов в зависимости от изменения расстояния от центра инструмента до вершины режущих кромок.
Результаты расчета изменения кинематических переднего и заднего углов в зависимости от вылета режущих кромок инструмента
|
d, мм |
43,5 |
42,5 |
40 |
39 |
38 |
|
Ψтеор., ° |
4,6 |
3,85 |
3,1 |
2,3 |
1,5 |
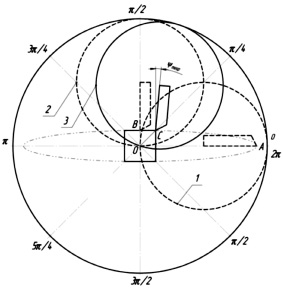
Рис. 1. Схема перемещения вершины режущей кромки инструмента в процессе обработки: ψтеор – величина изменения кинематического переднего угла инструмента; О – центральная точка; 1 – положение резцового блока в точке начала перемещения режущего инструмента; А – точка начала перемещения вершины режущей кромки; 2 – положение резцового блока в точке, в которой кинематические углы равны геометрическим; В – точка вершины режущего инструмента, в которой кинематические углы равны геометрическим; 3 – положение резцового блока в момент врезания; С – точка вершины инструмента в момент врезания
Зависимость имеет линейный характер и показывает, что с увеличением расстояния от центра инструмента до вершины режущих кромок величина изменения рабочих кинематических переднего и заднего углов уменьшается и наоборот.
На основании полученной ранее эмпирической формулы для определения изменения кинематических переднего и заднего углов инструмента [9] были построены графики сравнения теоретических и экспериментальных исследований.
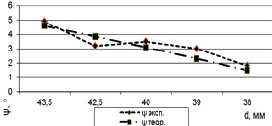
Рис. 2. График зависимости изменения кинематических переднего и заднего углов инструмента от расстояния между вершиной режущей кромки и осью вращения инструмента
Сравнительный анализ показал, что разность между экспериментальными и теоретическими значениями не превышает 10 %, что подтверждает адекватность полученных математических зависимостей.
Таким образом, полученная аналитическая зависимость позволяет определить изменение кинематических переднего и заднего углов в процессе формообразования наружных гранных поверхностей с переменным профилем планетарным точением и назначить их рациональные параметры с учетом технологических режимов обработки.
Работа выполнена в рамках гранта Президента РФ МК-2653.2014.8.
Рецензенты:
Кобелев Н.С., д.т.н., профессор, заведующий кафедрой теплогазоснабжения и вентиляции, ЮЗГУ, г. Курск;
Серебровский В.В., д.т.н., профессор, заведующий кафедрой информатики и прикладной математики, ЮЗГУ, г. Курск.
Работа поступила в редакцию 21.03.2014.