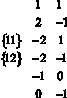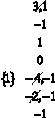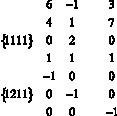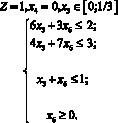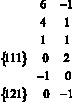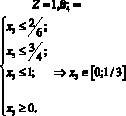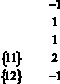Используемый в работе метод решения задач линейного программирования был впервые предложен российским математиком С.Н. Черниковым [3]. Кратко суть его сводится к следующему: сначала все ограничения задачи, состоящие из уравнений и неравенств, приводятся к единой системе неравенств одного смысла. Равенство для целевой функции Z можно, как показано далее, также свести к неравенству. В итоге получится система линейных неравенств относительно (n + 1) переменных x1, x2, ..., xn, Z или n переменных x1, x2, ..., xn и параметра Z. Далее последовательным исключением переменных по методу Жордана‒Гаусса приводим систему неравенств к окончательному виду Z m ≤ Z или Z ≤ M, где m, M (m ≤ M) – некие числа. Отсюда находится Zmin = m или Zmax = M. Подставляя после этого во все промежуточные неравенства вместо Z m или M, можно последовательно найти значения всех переменных x1, x2, ..., xn, обеспечивающих экстремум целевой функции Z. При необходимости этим же способом можно найти границы изменения каждой переменной xi.
В качестве примера рассмотрим решение системы неравенств
 (1)
(1)
Процесс исключения будем оформлять в табл. 1 как при решении систем уравнений методом Жордана‒Гаусса [1, 5].
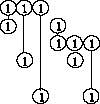
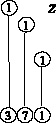
Слева в строках записаны коэффициенты перед x1 и x2 для каждого неравенства системы. Значок ∇ указывает, что исключается x2. Знак неравенства ≤ между левой и средней частью таблицы подразумевается. Справа положительные цифры в кружках означают умножение на них неравенств-строк. Прямая, соединяющая два кружка, указывает на последующее сложение этих строк. Порядок выбираемых пар строк несущественен, но должны быть выбраны все возможные пары. В блоке II слева 1-я строка – результат первого сложения, 2-я строка – второго и т.д. Последняя 7-я строка повторяет 5-ю строку блока I, так как в ней также отсутствует x2. Нули на месте исключённой x2 не пишем. Можно также сократить строки блока II на положительные числа. В правой части блока II выписана система неравенств для x1 в обычном виде. Её решение соответствует рис. 1.
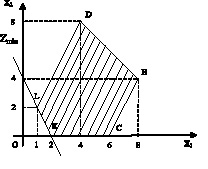
Рис. 1
Таблица 1
|
x1 x2 |
|
|
|
|
[I] |
|
|
|
|
[II] |
|
|
|
Далее найдем значение x2, отвечающие x1min = 1. Для этого подставим во все неравенства предыдущего блока I x1 = 1.
Получим:
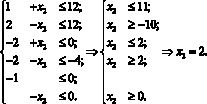
Нахождение x2 можно заметно упростить. Для этого отметим цифрами {11} и {12} слева в блоке I те неравенства, которые формируют конечное неравенство x1 ≥ 1, отмеченное в блоке II цифрой {1} слева. Подставим в них x1 = 1 и найдём x2:
![]()
Ещё проще вместо этой системы решить одно из соответствующих уравнений, например:
–2 + x2 = 0 ⇒ x2 = 2.
Это решение записано в блоке I справа.
Линейные неравенства с n переменными. Сформулируем теперь общие правила нахождения наименьших и наибольших значений переменных в произвольной системе линейных неравенств одного знака:
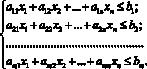 (2)
(2)
Любое решение (2) принадлежит области пересечения всех полупространств, задаваемых неравенствами (2). Эта область допустимых решений является выпуклым n-мерным многогранником [1, 2]. Его можно рассматривать как общее множество точек пересечения всевозможных пар полупространств, так как если решение (x1, x3, ..., xn) удовлетворяет каждой паре неравенств, то оно удовлетворяет всей системе пар (2), и наоборот. Отсюда следует, что проекция многогранника на координатную плоскость состоит из общих точек проекций пересечения каждой пары полупространств.
Проектирование пересекающейся пары полупространств, например, вдоль оси Ox1 на плоскость Ox2x3...xn, аналитически сводится к исключению переменной x1 из пары соответствующих неравенств (2). Поэтому проекции всего многогранника на плоскость Ox2x3...xn отвечает система всех неравенств-следствий с исключённой переменной x1. Проектируя далее полученную проекцию, т.е. исключая следующую переменную, получим систему неравенств-следствий с меньшим числом переменных. Очевидно, что на каждом этапе лучше исключать ту переменную, которая приведёт к меньшему количеству неравенств-следствий. Если удастся довести этот процесс до последней переменной, то найдём пределы её изменения. Затем, подставляя наименьшее или наибольшее значение этой переменной во все промежуточные системы и двигаясь снизу вверх, можно найти соответствующие значения остальных переменных.
Решение задач линейного программирования с ограничениями в виде системы неравенств. В самом общем случае задача линейного программирования выглядит так [1, 2]:
![]()
 (3)
(3)
Обычно к ограничениям (3) добавляют условия неотрицательности переменных: xi ≥ 0. Можно считать, что такие дополнительные неравенства в виде –xi ≤ 0 также входят в систему неравенств (3). В симплекс-методе решения задач линейного программирования все ограничительные неравенства за счёт введения вспомогательных неотрицательных переменных переписывают в виде уравнений. В излагаемом же методе, наоборот, систему уравнений (3) следует преобразовать в систему неравенств. Для этого систему уравнений (3) сначала нужно методом Жордана‒Гаусса привести к разрешённому виду, например, такому:
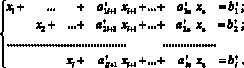
Отсюда выражаем разрешённые переменные:
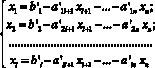
и подставляем их в целевую функцию Z(x1, x2, ..., xl, xl+1, x l+2, ..., xn) и во все неравенства (3). В итоге приходим к задаче линейного программирования с меньшим числом n – 1 переменных, удовлетворяющих только системе неравенств. Далее равенство для целевой функции заменяем линейным неравенством с параметром Z или с дополнительной переменной xn+1 = Z. В задачах на минимум ![]() а в задачах на максимум
а в задачах на максимум ![]() Окончательно задачи на минимум и на максимум примут вид:
Окончательно задачи на минимум и на максимум примут вид:
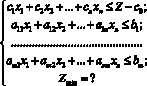 (4)
(4)
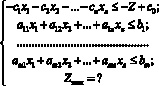 (5)
(5)
Следующий пример, взятый из [4], интересен тем, что симплексный метод его решения может привести к зацикливанию. При решении же методом неравенств (исключений) никаких особенностей не наблюдается.
![]()
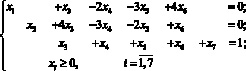 (6)
(6)
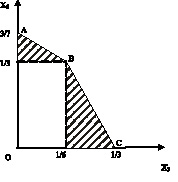
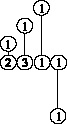
Рис. 2
Отбрасывая здесь неотрицательные разрешённые переменные x1, x2, x7, приведём (6) к виду системы неравенств (5):
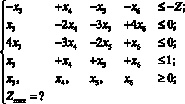 (7)
(7)
Решением правой части системы неравенств блока II является четырёхугольник ABCO на рис. 2. Координаты любой его точки находятся через координаты его вершин ![]()
![]()
![]() O(0; 0)
O(0; 0)
по формуле (1), (6):
![]()
где 0 ≤ α, β, γ, δ ≤ 1, α + β + γ + δ = 1.
Таблица 2
|
x3 x4 x5 x6 |
|
|
|
|
[I] |
|
|
|
|
[II] |
|
|
|
|
[III] |
|
|
|
|
[IV] |
|
|
|
|
[V] |
|
|
|
Отсюда:
![]()
![]()
![]() (8)
(8)
Согласно правой стороне блока I:
![]() (9)
(9)
Из (7) с учетом (8), (9) и x4 = 0 находятся остальные переменные:
![]()
![]()
x7 = 0.
Рецензенты:
Туганбаев А.А., д.ф.-м.н., профессор кафедры высшей математики Национального исследовательского университета МЭИ,
г. Москва;
Титов В.А., д.э.н., профессор, начальник отделения факультета математической экономики и информатики РЭУ им. В.Г. Плеханова, г. Москва.