Модели динамики пространственно распределённых биологических сообществ часто основываются на уравнениях «реакция‒диффузия», которые требуют, чтобы особи перемещались по пространству случайно и бесцельно. Модели динамики на основе принципа эволюционной оптимальности [2, 3] свободны от этого противоречия: перемещения особей носят целенаправленный характер и должны максимизировать средний по пространству коэффициент размножения (КР). Однако открытым остаётся вопрос о том, какой информацией располагают особи, принимая решение о перемещении. В зависимости от количества информации рассматривают модели:
– глобальной информированности – особям известна вся информация о состоянии окружающей среды в месте их пребывания, а также в стации эмиграции, информация о численностях субпопуляций в обеих стациях и цена перемещения (т.е., затраты на перемещение из стации в стацию, выраженные в долях КР);
– полной неинформированности;
– локальной информированности, в которой особи располагают частичной информацией, необходимой для принятия решения о миграции.
Модели глобальной информированности были рассмотрены ранее [3–6]. В настоящей работе будет рассмотрена модель с локальной информированностью особей.
Модель оптимизационной
миграции с локальной
информированностью особей
Будем рассматривать двухвидовое сообщество, особи в котором взаимодействуют по типу «хищник–жертва». Оба вида
распределены по двум стациям; ситуацией миграции будем считать перемещение особей какого-либо вида (или двух сразу) из одной стации в другую. Все остальные перемещения внутри стаций, в реальной ситуации неизбежные, миграцией считаться не будут и (по предположению) не будут оказывать влияния на динамику сообщества. Будем рассматривать динамику в дискретном времени. Дискретный характер модели в части пространственного поведения обусловлен также биологическими соображениями: едва ли можно ожидать, что инфинитезимальные перемещения особей в пространстве (составляющие подавляющее большинство перемещений в рамках диффузионных моделей) дадут выигрыш больший, чем сами затраты на перемещения.
Пусть динамика сообщества в каждой из стаций (в отсутствие миграции) описывается разностным аналогом классического уравнения Лотки‒Вольтерры:
![]() (1)
(1)
где Nn(Xn) – численность жертв (хищников) в момент времени n; a характеризует плодовитость популяции жертв (среднее число потомков в следующем периоде при условии отсутствия внешних воздействий и давления хищников); b характеризует площадь, которая необходима особи жертвы для нормального воспроизводства; h аналогичен b, но характеризует хищников; параметр f описывает успешность поиска и атаки хищниками жертв, а также успешность использования жертвами убежищ либо защиты; ε – параметр, характеризующий эффективность превращения биомассы жертв в биомассу хищников (0 < ε < 1).
В случае наличия миграции жизненный цикл разделен на два этапа – размножение и миграция; они независимы и протекают поочередно: на каждом шаге времени происходит перераспределение особей между стациями (если оно имеет место), а затем – размножение.
В нашей работе рассмотрен случай, в котором локальная информированность понимается как знание особями условий существования в стации пребывания, а также знание текущей численности всех субпопуляций, населяющих стацию пребывания, на которые они и ориентируются. При этом состояние окружающей среды и значения численностей любых субпопуляций в стации иммиграции считаются неизвестными. Особи мигрируют, если их число превышает некоторую оптимальную численность. Оптимальная численность – это такая численность, которая обеспечивает максимальную рождаемость (число потомков в первом поколении) вида на следующем шаге. Это предположение справедливо всегда, когда фертильность (рождаемость), т.е. число потомков в следующем поколении является немонотонной функцией численности соответствующей субпопуляции [1].
Зависимость численности субпопуляции (для определенности) жертв в следующем поколении от численности жертв в текущем поколении в соответствии с формулой (1) определяется формулой
![]()
Максимальное значение численности Nn+1(Nn) может быть легко определено. Пусть ![]() – оптимальная численность жертв на шаге n, тогда
– оптимальная численность жертв на шаге n, тогда
![]()
откуда
![]() и
и ![]()
Следовательно, особи мигрируют, если оптимальная численность меньше текущей численности особей, т.е. ![]() .
.
Для хищников оптимальная численность и величина миграционного потока вычисляются аналогично:
![]() и
и ![]()
Модель работает следующим образом: на каждом шаге времени n определяются величины миграционных потоков Θ и Δ, для хищников и жертв соответственно. Затем происходит перераспределение особей между стациями. После него идёт размножение в силу уравнений (1), после чего весь цикл повторяется снова.
Например, для случая перемещения из второй стации в первую имеем
![]()
и
![]()
где p и q – коэффициенты перемещения для жертв и хищников соответственно (0 ≤ p ≤ 1, 0 ≤ q ≤ 1). Эти коэффициенты могут быть интерпретированы как вероятность успешного перемещения из стации
в стацию без ущерба для дальнейшего
размножения.
По-видимому, самым важным эффектом локальной информированности на динамику численности оптимально перемещающихся особей, который обнаруживается в моделях подобного рода, следует считать эффект встречных миграций: в любой момент времени миграция может происходить в обоих направлениях, если превышены пороговые численности
в обеих стациях.
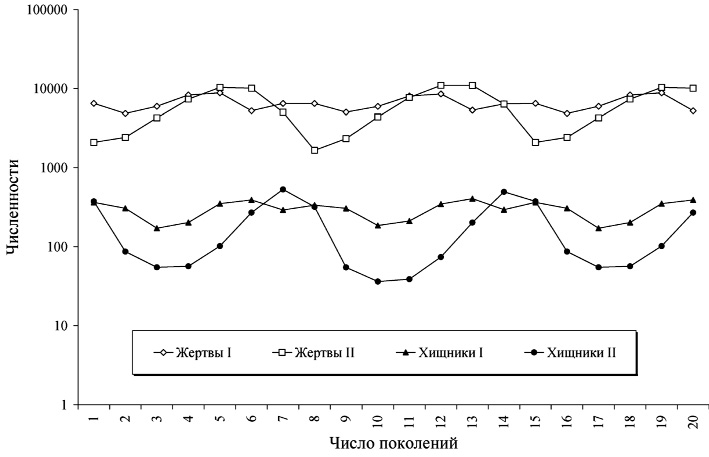
Рис. 1. Пример динамики двухвидового сообщества, занимающего две стации и реализующего стратегию оптимального пространственного перемещения при локальной информированности особей каждого из видов. Значения параметров: aI = 2,5, bI = bII = 0,0001, fI = 0,003,
aII = 2,3, fII = 0,0028, hII = 0,0008, ε = 0,09, p = 0,5, q = 0,5.
Численности особей показаны в логарифмической шкале
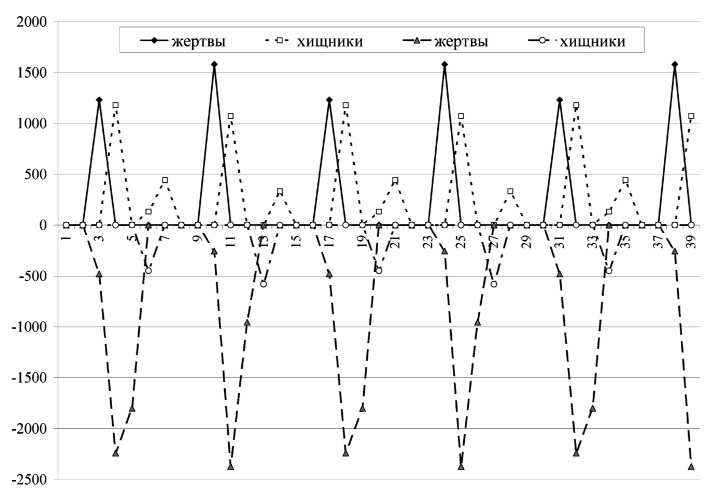
Рис. 2. Миграционные потоки жертв и хищников для набора параметров, указанного на рис. 1
Например, для перемещения жертв:
![]()
и
![]()
где
![]()
а для перемещения хищников:
![]()
и
![]()
где
![]()
Затем, как говорилось выше, происходит размножение в силу системы уравнений (1) с теми численностями, которые складываются в результате перераспределения особей, то есть ![]() .
.
На рис. 1 показан пример динамики такой модели: цикл длины 14, что является нетипичным для динамики пространственно распределенных сообществ: в случае отсутствия миграции: область устойчивости для такого режима чрезвычайно мала. На рис. 2 показаны миграционные потоки для того же режима, что и на рис. 1. Значения миграционных потоков в разные стации показаны разными знаками; сами по себе миграционные потоки, безусловно, положительны. Значения миграционных потоков для хищников увеличены в 10 раз для наглядности.
Сравнение оптимизационной и диффузной миграции
Модели локальной информированности можно сравнить с диффузионными моделями. Для нашего случая (ящичная миграция) диффузионное приближение состоит в случайном блуждании особей между тремя узлами, два из которых соответствуют стациям, а один – перемещению для случая цены перемещения р < 1. Кроме того, диффузионное приближение требует определения собственно процесса диффузии: каково должно быть распределение вероятностей эмиграции k особей? В рамках настоящей статьи мы использовали равномерное по интервалу [0, Nn] распределение.
В таблице показаны средние по 1000 поколениям значения численностей жертв и хищников в каждой из стаций; в левой части таблицы представлены расчёты для модели локальной информированности, в правой – для диффузионной миграции. Один из параметров (aI) менялся в указанных в таблице пределах, все остальные были такими же, как на рис. 1.
Сравнение динамики локально информированных особей и диффузионной миграции. Xi(Ni) – численность хищников (жертв) в i-й стации, угловыми скобками показаны
средние для ста реализаций диффузионной миграции
|
aI |
NI |
NII |
XI |
XII |
⟨NI⟩ |
⟨NII⟩ |
⟨XI⟩ |
⟨XII⟩ |
|
2 |
5192,91 |
6093,82 |
162,73 |
20,29 |
7190,91 |
9136,14 |
26,83 |
31,39 |
|
2,1 |
5337,38 |
6112,33 |
192,68 |
210,50 |
7702,20 |
9015,78 |
41,09 |
46,29 |
|
2,2 |
5574,67 |
6030,9 |
219,74 |
210,92 |
8385,42 |
9096,10 |
48,02 |
52,82 |
|
2,3 |
5834,47 |
6154,03 |
246,91 |
204,47 |
9344,17 |
9379,46 |
45,29 |
48,59 |
|
2,4 |
6180,12 |
6218,34 |
272,29 |
197,57 |
10123,20 |
9443,52 |
50,74 |
52,86 |
|
2,5 |
6564,23 |
6130,96 |
296,73 |
192,41 |
11376,30 |
9861,63 |
38,63 |
39,21 |
|
2,6 |
7068,70 |
5840,50 |
307,39 |
214,05 |
12656,50 |
10224,00 |
26,98 |
26,64 |
|
2,7 |
7744,96 |
5755,85 |
308,49 |
222,85 |
13898,30 |
10476,20 |
18,17 |
17,51 |
|
2,8 |
19186,3 |
12196,10 |
10,62 |
8,33 |
15006,30 |
10572,00 |
14,33 |
13,44 |
|
2,9 |
20779,7 |
12037,40 |
6,49 |
3,87 |
16232,80 |
10700,80 |
7,22 |
6,59 |
Динамика для диффузионного и целенаправленного перемещения особей, показанная в таблице, существенно различается. Дело в том, что для моделей диффузионной миграции наверняка наступает вымирание хищников при aI > 2,2, в то время как для целенаправленной миграции такое вымирание наступает лишь при aI > 2,8. В таблице отсутствуют нулевые значения численностей для тех наборов параметров, при которых наблюдается вымирание. Это связано с тем, что осреднение проводилось по всему временному диапазону, включая релаксационные процессы.
Следует подчеркнуть, что совпадение либо различие предельных динамических режимов в моделях оптимизационной и диффузионной миграции не может служить критерием правильности модели либо её преимуществ: это связано с тем, что для моделей подобного рода всегда можно найти область существования сколь угодно сложного предельного динамического режима. Главным преимуществом модели оптимизационной миграции является отказ от предположения о случайности и бесцельности перемещения особей. Кроме того, модель с локальной информированностью обладает ещё одним важным свойством: она существенно расширяет области устойчивого существования циклов длины, кратной простым числам > 5.



