Уменьшение геометрических размеров элементов интегральных микросхем породило в микро-системотехнике фундаментальную проблему создания планарной индуктивности, которая бы в малых размерах имела приемлемые значения для построения сложных функциональных блоков и IP-модулей, работающих на Гигагерцах [2,3].
Оценки индуктивностей с использованием известных математических методов расчёта, разработанных Калантаровым П.Л. и Цейтлиным А.А. [1] в 70-х годах прошлого века, в микрометровом диапазоне геометрических размеров могут приводить к отрицательным значениям индуктивности.
Обнаруженный недостаток геометрической теории потребовал создания принципиально новых физико-математических моделей, которые были бы ориентированы на потребности планарной технологии.
Ниже предлагается оригинальная методика расчётов спиральной индуктивности L высокой симметрии, исходящая из физического определения этого понятия как коэффициента пропорциональности между потоком Ф и током i, создающим этот поток [4]
Ф = Li. (1)
В связи с этим предлагаемая последовательность расчёта индуктивности плоской токовой спирали заключается в следующем:
1) по заданному значению тока в кольце радиусом R рассчитывается значение магнитного поля B* в центре кольца;
2) в это кольцо помещается спираль с заданным законом зависимости r = r(φ) в полярных координатах, который ограничен по числу витков N двумя переменными: начальным значением угла φ1 и радиусом r1 и конечным значением угла φ2 и радиусом r2 = R, совпадающим с радиусом кольца;
3) по закону Био‒Савара‒Лапласа рассчитывается новое значение индукции магнитного поля B, которое создаёт ограниченная планарная спираль в центре кольца;
4) вычисляется коэффициент увеличения индукции магнитного поля a = B/B* и находится связь значения индуктивности, формируемого спиралью, с коэффициентом увеличения индукции a.
Физико-математическая модель расчёта
Одним из мощных методов расчета магнитостатических полей по праву считается закон Био‒Савара‒Лапласа [4]. Он позволяет выяснить физические закономерности распределения магнитных полей, создаваемых простейшими токовыми системами. В современных математических обозначениях он записывается в виде
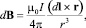 (2)
(2)
где dB – элементарная магнитная индукция поля, создаваемая элементом проводника с током Idl, μ0 = 4π∙10–7 Гн/м – магнитная постоянная; dl – элементарный вектор длины, совпадающий по направлению с током (элемент проводника); I – сила тока; r – радиус-вектор, проведенный от элемента проводника к точке наблюдения A, в которой определяется магнитная индукция.
Магнитное поле тока в центре спирали Архимеда
Расчёт магнитного поля в центре спирали будем проводить, используя закон (2). На рисунке представлено расположение векторов задачи. Направление векторов и сами векторы отмечены стрелками. На рисунке представлены декартовая и полярная системы координат. Жирная кривая выделяет фрагмент спирали, которая начинается в точке (0,0). Вектор dl направлен по касательной к выделенной кривой и совпадает с направлением тока. Он имеет две компоненты dlII и dl^. Вектор dl составляет угол a с направлением радус-вектора r. Вектор dl составляет угол α1 с направлением другого вектора r1. Векторы r и r1 – противоположны друг другу, но равны по модулю.
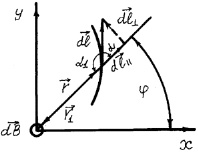
Направление основных векторов задачи
На плоскости, представленной на рисунке, закон (2) можно записать в скалярном виде
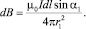 (3)
(3)
Затем в (3) следует замена
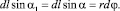 (4)
(4)
Она указывает на то, что поперечная составляющая вектора dl^ вносит вклад в формирование индукции магнитного поля в начале координат, а продольная составляющая dlII – не вносит. Тогда формула для расчёта элементарной индукции магнитного поля в центре спирали имеет вид
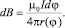 (5)
(5)
Из (5) следует общая формула для расчёта индукции в начале координат для любых спиралей, имеющих закон, представленный в полярных координатах r = r(φ),
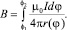 (6)
(6)
Рассчитаем коэффициент увеличения индукции в центре спирали Архимеда. Уравнение спирали Архимеда имеет вид [5]
r = aφ, (7)
где a – постоянная. Как известно, спираль Архимеда описывает движение точки, которая имеет две компоненты скорости – постоянную радиальную скорость движения υr и постоянную угловую скорость w. Постоянная a связана с этими переменными соотношением a = υr/ω.
Предположим, что начальное положение спирали Архимеда находится в точке r = r1 и имеет угол φ1 = p/2. Это позволяет устранить особенность, возникающую в начале координат. Тогда начальный и конечный радиусы и начальный и конечный угол спирали связаны соотношением
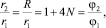 (8)
(8)
где N – целое количество витков спирали.
Интегрируя в этих пределах выражение (6), получим выражение для коэффициента увеличения индукции поля a, который зависит только от числа витков N
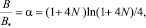 (9)
(9)
где 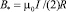 (10)
(10)
– масштаб индукции, создаваемый в центре кольца тем же током.
В табл. 1 представлена зависимость коэффициента увеличения индукции a и отношения конечного радиуса к начальному R/r1 от числа витков спирали Архимеда.
Таблица 1
Зависимость коэффициента увеличения индукции от числа витков спирали Архимеда
|
N |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
|
α |
4,94 |
8,33 |
12,04 |
15,98 |
20,12 |
24,41 |
28,85 |
33,40 |
38,06 |
89 |
|
R/r1 |
9 |
13 |
17 |
21 |
25 |
29 |
33 |
37 |
41 |
81 |
Из табл. 1 видно, что увеличение числа витков от 2 до 20 позволяет увеличить индукцию магнитного поля в центре спирали Архимеда от 5 до 90 раз.
Магнитное поле тока в центре обобщённой спирали
Для обобщённых спиралей вида
r = aφn, (11)
где n – любое число, кроме единицы, возможны следующие классы спиралей. Класс спиралей отрицательных порядков n < 0 (класс закручивающихся спиралей), класс дробных положительных порядков 0 < n < 1 и класс спиралей положительных порядков 1 < n < ∞. Последние два класса относятся к классу раскручивающихся спиралей.
Подставляя (11) в интеграл (6), для коэффициента увеличения индукции поля получим соотношение
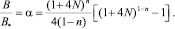 (12)
(12)
Связь начальных и конечных переменных получается в виде
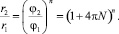 (13)
(13)
В табл. 2 представлены зависимости коэффициента увеличения индукции, a в центре обобщённой спирали для разных индексов n. Первые две строки рассчитаны для n = 1/2, Вторые две строки рассчитаны для n = 3/2, а последние две строки рассчитаны для n = 2.
Таблица 2
Зависимость коэффициента увеличения индукции от числа витков обобщённых спиралей для разных n
|
N |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
20 |
|
a(n1) |
3,0 |
4,7 |
6,5 |
8,2 |
10,0 |
11,8 |
13,6 |
15,5 |
17,3 |
36.0 |
|
R/r1 |
3,0 |
3,6 |
4,1 |
4,6 |
5,0 |
5,4 |
5,7 |
6,1 |
9,0 |
27,0 |
|
a(n2) |
9,0 |
16,9 |
26,5 |
37,6 |
50,0 |
63,6 |
78,3 |
94,0 |
110 |
324 |
|
R/r1 |
27 |
46,9 |
70,0 |
96,2 |
125 |
156 |
190 |
225 |
262 |
729 |
|
a(n3) |
18 |
39 |
68 |
105 |
150 |
203 |
264 |
333 |
410 |
1620 |
|
R/r1 |
81 |
169 |
289 |
441 |
625 |
841 |
1089 |
1369 |
1681 |
6561 |
Из табл. 2 видно, что наиболее перспективными являются раскручивающиеся спирали с показателем n > 1. Для рассчитанных значений полученные коэффициенты увеличения индукции для одного и того же количества витков N всегда больше, чем у спирали Архимеда. Но, с другой стороны, большие коэффициенты a можно получить только путём увеличения эффективной площади, занимаемой обобщённой спиралью.
Считая, что среднее значение потоков индукции в кольце и спирали можно рассчитывать по значениям индукции в центре, получим оценочное соотношение для коэффициента увеличения индуктивности, который совпадает с коэффициентом увеличения индукции
L = αL*, (14)
где L* = μ0πR/2 (15)
– масштаб индуктивности.
Проведём оценку для N = 10 витков спиральной индуктивности, начальный радиус, которой 10 мкм. Для спирали Архимеда конечный радиус 410 мкм (см. табл. 1), масштаб индуктивности 0,81 нГн, а увеличение индуктивности происходит почти в 40 раз до значений 30,8 нГн. Для спирали того же начального радиуса с n = 2 получим конечный радиус 16,8 мм, (см. табл. 2 и соотношение (13)), масштаб индуктивности 33,2 нГн, а увеличение индуктивности происходит почти в 1680 раз до значений 55,8 мкГн.
Выводы
- Предложен оценочный метод расчёта планарной индуктивности спирального вида.
- Метод базируется на законе Био‒Савара‒Лапласа, который позволяет в полярных координатах рассчитывать индукцию в центре для любых видов спиралей.
- Проведена сравнительная оценка значений спиральной индуктивности для спиралей Архимеда и обобщённых спиралей.
- Показано, что применение спиралей с количеством витков N = 10 может увеличивать значение их индуктивности по сравнению с кольцевой от 40 до 1500 раз.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант № 12-08-00654/12 (2012-2013 гг.).
Рецензенты:
Бубнов В.А., д.т.н., профессор, заведующий кафедрой естественнонаучных дисциплин, ГБОУ ВПО «Московский городской педагогический университет», г. Москва;
Крутчинский С.Г., д.т.н., профессор кафедры систем автоматического управления, ФГАОУ ВПО «Южный федеральный университет», г. Ростов-на-Дону.
Работа поступила в редакцию 25.12.2013.



