Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

В работе рассматривается сложная техническая система, состоящая из n элементов. Каждый элемент, а значит, и система в целом характеризуется тремя основными параметрами: вероятностью безотказной работы, стоимостью и средним временем безотказной работы. Пусть pj – вероятность безотказной работы j-го элемента, sj – стоимость j-го элемента, tj – среднее время безотказной работы j-го элемента, j ∈ {1, 2, ..., n}. В целях улучшения характеристик всей системы используют резервирование элементов. В промышленной автоматизации наибольшее распространение получили следующие методы резервирования: резервирование замещением «один из двух» (1оо2 – 1 out of 2) и метод мажоритарного голосования «два из трех» (2оо3) [1]. Системы без резервирования классифицируются как 1оо1.

Таблица 1

Зависимость параметров j-го элемента системы от способа резервирования

Через Gj обозначен коэффициент, увеличивающий стоимость схемы 1оо2, если для данного резервируемого элемента существует надежный блок переключения на резерв. В случае, если для каких-либо элементов такой блок отсутствует, для них вводится запрет на возможность быть зарезервированными методом 1оо2. Обозначим множество номеров таких элементов через I. Имеется ограничение на среднее время безотказной работы резервируемой системы: оно должно быть не меньше заданного значения.

Задача состоит в выборе способа резервирования для каждого элемента системы, который позволил бы получать наибольшую возможную вероятность безотказной работы при наименьшей стоимости с учетом выполнения ограничения на среднее время безотказной работы системы. Математическая модель бикритериальной задачи оптимального резервирования имеет вид:

(1)

(2)

(3)

(4)

xij ∈ {0, 1} ; (5)

x2j = 0 . (6)

Обозначения:

Здесь i ∈ {1, 2, 3} – номер способа резервирования (соответственно 1оо1, 1оо2, 2оо3). Ptotal – вероятность работы без отказа всей системы, Stotal – общая стоимость системы. Tmin  – минимальное среднее время работы до отказа всей системы. Ограничение (3) имеет соответствующий вид потому, что среднее время работы до отказа всей системы связано со средним временем наработки до отказа ее элементов следующим соотношением:

Отметим, что с целью получения более простой однокритериальной модели задачи можно было бы отказаться от целевой функции (2), добавив соответствующее ограничение на итоговую стоимость системы. Однако в данном случае существует несколько практических доводов в пользу рассмотрения именно бикритериальной модели. Во-первых, стоимость сложной технической системы является довольно высокой и может варьироваться в достаточно широких пределах. В связи с этим имеет смысл отыскания всего множества парето-оптимальных решений бикритериальной задачи (или хотя бы его представительной аппроксимации), чтобы получить представление о возможных диапазонах изменения стоимости и надежности и иметь возможность выбрать в итоге компромиссный вариант. Во-вторых, задача конструирования такого рода системы является технически сложной и содержит ряд трудноформализуемых требований (в частности, ограничение на габариты). Поэтому получение не одного, а сразу множества решений позволит выбрать из них наиболее приемлемое с конструкторской точки зрения.

Анализ задачи

Изучим более подробно, как влияет способ резервирования элементов на их характеристики. Рассмотрим, как влияет вариант резервирования j-й детали на вероятность ее безотказной работы (здесь и далее j ∈ {1, 2, ..., n}, если не оговорено другое). Пусть исходное значение этого параметра – pj. Введем обозначения: P1(pj) = pj, , – вероятность безотказной работы j-го элемента при способе резервирования 1оо1, 1оо2 и 2оо3 соответственно. Построим график зависимости получаемого значения вероятности безотказной работы при определенном виде резервирования от исходного значения этого показателя (рисунок). Вообще говоря, по свойству вероятности, pj ∈ [0, 1]. Однако, исходя из прикладного смысла задачи, можно полагать, что pj достаточно близко к 1. Поэтому достаточно рассматривать случаи (точка является точкой пересечения графиков P1(pj) и P3(pj)). Из графика видно, что в таком случае Таким образом, наибольшую вероятность безотказной работы дает способ резервирования 1оо2. Однако следует помнить, что этот способ резервирования не всегда возможен, и тогда лучший показатель дает способ резервирования 2оо3.

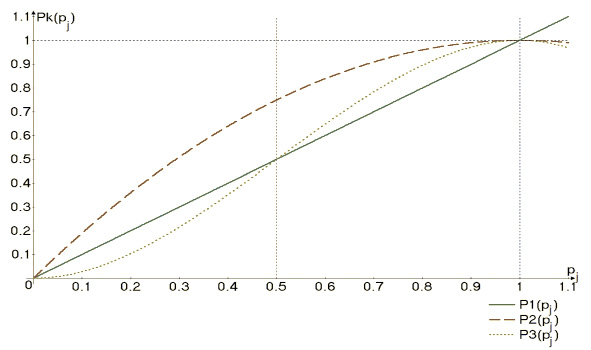
График зависимости получаемой в результате резервирования вероятности безотказной работы элемента от исходного значения данного параметра

По аналогии рассмотрим, как влияет способ резервирования на стоимость элемента. Пусть исходная цена j-го элемента – sj. Обозначим S1(sj) = sj, S2(sj) = 2Gjsj, S3(sj) = 4sj – стоимость j-го элемента при применении к ним способа резервирования 1оо1, 1оо2 и 2оо3 соответственно. Так как Gj ≥ 1, то самый лучший показатель в плане цены обеспечивается при способе резервирования 1оо1. Рассмотрим ограничение на среднее время работы системы до отказа. Пусть среднее время работы элемента до отказа равно tj. Введем обозначения:

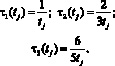
Очевидно, что . Таким образом, значение τ2(tj) является самым малым, однако способ резервирования 1оо2 не всегда возможен. В этом случае самым малым будет значение τ1(tj). С учетом приведенных выше заключений будет строиться алгоритм метода ветвей и границ для решения данной задачи.

Метод ветвей и границ для решения задачи повышения надежности резервирования

Метод ветвей и границ основан на ветвлении, т.е. разбиении множества допустимых решений на подмножества и нахождении оценок, с помощью которых дерево поиска может усекаться, сокращая область поиска решений.

Ветвление. Пусть множество всех возможных решений (без учета ограничения на среднее время работы до отказа) – Ω. В данной задаче можно воспользоваться следующим правилом ветвления:

,

где Ωi = {x ∈ Ω: xik = 1, xjk = 0 для j ≠ i}, где j, i ∈ {1, 2, 3}, k – некоторый фиксированный номер координаты, k ∈ {1, 2, ..., n}. (Иначе говоря, Ωi – это подмножество множества допустимых решений, в котором для резервирования элемента k выбран способ i). Затем рассматриваются полученные подмножества Ωi и также разбиваются на основе значений очередной координаты вектора решения x. Если способ резервирования 1оо2 для соответствующего элемента невозможен, то полагается Ω2 = ∅, т.е. дальнейшее рассмотрение этого множества не требуется. Разбиение множества решений продолжается до тех пор, пока получившиеся подмножества содержат больше одного возможного решения. Если подмножество содержит одно возможное решение, то это решение подлежит проверке на включение в рекордное множество.

Построение множества рекордных решений. Пусть вектор – способ резервирования, назначенный для j-го элемента. Тогда возможное решение представимо в виде

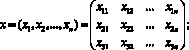
если j-му элементу назначается способ резервирования 1оо1; если – 1оо2, если – 2оо3. Т.е. , причем при j ∈ {1, 2, ..., n}/I xij ∈ {0, 1}; при j ∈ I только для i ∈ {1, 3} xij ∈ {0, 1}, а x2j = 0. Будем говорить, что решение доминирует решение , и писать , если или . Если , то будем говорить, что решения и равносильны, и писать . Если для решения из некоторого множества возможных решений не существует возможных решений , таких что , то решение будем называть недоминируемым в множестве . Множество рекордных решений для данной задачи представляет собой совокупность таких решений, которые являются недоминируемыми в множестве всех рассмотренных на данный момент возможных решений. Рассмотрим подробно процесс формирования такого множества. Пусть на какой-то момент работы алгоритма имеется некоторое множество рекордных решений R и получено новое допустимое решение xnew, т.е. оно удовлетворяет ограничению на среднее время работы до отказа всей системы (в противном случае это решение не рассматривается). Если , то решение xnew в рекордное множество не добавляется. Если же в R нет решений, доминирующих xnew, то xnew включается в множество R, причем из R убираются все решения, которые являются доминируемыми решением xnew. Следует отметить, что если и (т.е. ), то xnew также включается в множество R.

Оценка подмножеств допустимых решений и сокращение дерева поиска. Пусть рассматривается узел дерева, соответствующий подмножеству решений, для которых первые k координат определены, т.е. подмножеству – фиксированные векторы, k ∈ {1, 2, ..., n – 1} (отметим, что при k = n множество Ωcurr состоит из одного решения и смысла в подсчете оценок в этом случае нет). Найдем минимальное значение левой части неравенства (9) для решений, входящих в Ωcurr. Введем обозначения:

,

,

.

Тогда, исходя из приведенного выше анализа задачи, можно привести следующее равенство для искомого минимальное значения:

,

где .

Таким образом, если , то данный узел далее ветвить не имеет смысла, т.к. , т.е. ограничение на среднее время работы системы до отказа не выполняется для любого решения из рассматриваемого подмножества. Если же , то в Ωcurr содержатся элементы, которые имеют шанс войти в множество рекордных решений. В этом случае имеет смысл найти еще несколько оценок, с помощью которых также имеется вероятность сократить дерево поиска. Пусть

.

Тогда можно найти значение вероятности безотказной работы, выше которого элементы рассматриваемого подмножества решений обеспечивать не могут. Это значение можно определить следующей формулой:

,

где .

Значение стоимости системы, ниже которого решения из рассматриваемого подмножества обеспечить не могут, можно найти по следующей формуле:

,

где

,

. Таким образом, и . Полученные оценки дают шанс сократить дерево поиска. Если на рассматриваемый момент в множестве рекордных решений R находится такое решение x, что , то текущее подмножество возможных решений можно не рассматривать, так как любые элементы данного подмножества будут доминироваться решением x, то есть ни одно из них не сможет попасть в множество рекордных решений.

Алгоритм метода ветвей и границ для задачи повышения надежности резервирования

1. Инициализация. Положить Ωcurr = ∅, R = ∅, k = 0.

2.

3. Разбиение множества решений на подмножества по координате xk.

.

Если k ∈ I, то .

4. Для d = 1, 2, 3, если , то

а) вычислить . Если , то перейти к следующему значению d, иначе перейти к шагу б.

б) вычислить и . Если , то перейти к следующему значению d, иначе перейти к шагу в.

в) если k ≠ n, то перейти рекурсивно к шагу 3, иначе осуществить проверку включения полученного допустимого решения (при k = n множество состоит из одного элемента) в множество рекордных решений.

Стратегия обхода дерева вариантов

В процессе разработки описываемый алгоритм метода ветвей и границ был многократно протестирован с применением предварительного упорядочивания элементов по убыванию коэффициентов, вычисляемых на основе характеристик pj, sj и tj с целью определения наилучшего порядка перебора координат при ветвлении, то есть выбора стратегии обхода дерева вариантов. Коэффициенты целевых функций и ограничений определялись с помощью рандомизированной процедуры, рассматривались системы, содержащие от 20 до 50 элементов с возможностью резервирования. В табл. 2 приведен фрагмент результатов такого тестирования. Видно, что упорядочивание элементов по убыванию коэффициента sj/pj дает самые хорошие результаты, с помощью него время работы алгоритма сокращается в несколько раз. Таким образом, предварительное упорядочивание элементов по убыванию коэффициента sj/pj и последующее ветвление дерева вариантов в соответствии с полученной очередностью является мощным способом увеличения скорости поиска решения задачи повышения надежности резервирования с помощью предложенного метода ветвей и границ.

Зависимость времени выполнения (в мс) алгоритма от способа предварительной сортировки элементов

Рецензенты:

Азарнова Т.В., д.т.н., профессор, Воронежский государственный университет, г. Воронеж;

Чопоров О.Н. д.т.н., профессор, проректор по научной работе Воронежского института высоких технологий, г. Воронеж.

Работа поступила в редакцию 05.12.2013.