Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Федеральный закон № 261-ФЗ «Об энергосбережении и о повышении энергетической эффективности… Российской Федерации» стимулировал развитие возобновляемых источников электроэнергии (ЭЭ). Проблема ее выработки в системах автономных приборов и средств автоматики на трубопроводах, военных и метеорологических датчиков JPS-навигации, экологических устройств и др. в непрерывном режиме стоит остро.

В полевых условиях оптимальны компактные устройства электропитания на термоэлементах (ТЭ), основанные на эффекте Зеебека – преобразовании в ЭЭ естественных перепадов температур окружающей среды. Такие устройства могут найти применение в резко континентальных климатических зонах, в горах и пустынях.

Нами использовано теплоэкзо/эндо фазовых переходов (ФП в области температур (5–70 °С) окружающей среды. Это смеси парафинов, но они достаточно дороги. Альтернатива им – соли с гидратированной водой – кристаллогидраты. Это СаCl2⋅6H2O, сульфaт натрия, гипосульфит натрия и др. Характеристики СаCl2⋅6H2O и воды приведены в таблице.

Параметры, характеризующие кристаллогидраты

Однако процессы в ходе ФП изучены недостаточно, и Нобелевский лауреат В.Л. Гинзбург решение проблемы ставил в ряду важнейших. В данной работе нами ставилась задача изучения СаCl2⋅6H2O методами ядерной магнитной резонансной релаксометрии (ЯМРР) и термоэлектрической спектроскопии.

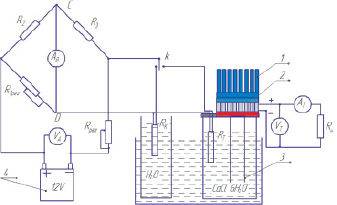
Рис. 1. Устройство для получения зависимости «температура – время», напряжение и ток ТЭ: 1 – радиатор; 2 – термоэлемент; 3 – термостат; 4 – аккумулятор 12 В с вольтметром VА, R2 и R3– прецизионные сопротивления в плечах моста Уинстона, R1рег – потенциометр для первоначального балансирования токов моста при комнатной температуре, Rрег – потенциометр для регулирования напряжения аккумулятора, Rн – электрическое сопротивление нагрузки Rт и Rк– термосопротивления для измерения температуры соли и воды, АВ амперметр для определения баланса токов моста, АТ и VТ – амперметр и вольтметр на термоэлементе для измерения тока и напряжения на ТЭ

Для анализа фазовых переходов используется обычная, дифференциальная сканирующая калориметрия (ДСК) и дифференциальный термический анализ (ДТА). Однако, как это отмечено в работе Zalba [8], имеется большая неопределенность характеристик образцов, полученных разными исследователями. Отмечены ограничения этих методов:

a) малые объемы образцов (1–10 мг), но некоторые свойства зависят от их количества;

б) аппаратура сложна и дорога;

в) ФП не могут быть визуально наблюдаемы.

Предложен [8] метод измерения энтальпии и теплопроводности из графиков температуры от времени путем сравнения их с графиками «температура-время» для эталонного вещества (напр. воды) с вычислением параметров ФМВ.

Следуя данным рекомендациям, нами разработано устройство для калориметрического анализа, приведенное на рис. 1. Температура в образце и эталонном веществе (воде) измеряется терморезисторами Rt = 50 Ом II класса точности (ошибка ∆t = ±(0,30 + 3,5∙10–3t), подключенными к мосту Уитстона, питаемому аккумулятором. Амперметр мостика позволяет устанавливать баланс ветвей моста, а мультиметр, подключенный к электродам, измеряет напряжение и ток ТЭ. Сопротивление в интервале –50 °С ≤ T ≤ + 180 °С определялось по формуле

Rt = Ro(1 + αT),

где a = 4,26∙10–3 К–1. Процессы ФП исследовались в диапазонах: температур 20–70 °С и времени до 360 минут. Объем образца 100 см3.

Для исследований ФП методом ЯМР-релаксометрии использовался лабораторный релаксометр ЯМР 09/РС, разработанный [3] на резонансную частоту νо = 9,2 МГц. Задание параметров импульсных последовательностей: Т – периода запуска; t – временного интервала между 90° и 180° импульсами; N – числа 180° импульсов; n – числа накоплений осуществляется через клавиатуру ЭВМ и высвечивается на мониторе. Минимальный интервал между импульсами t = 100 мкс, число импульсов N = 1000, накоплений – до 100. Время измерения с накоплением составляет в среднем не более 2–3 минут.

Погрешности однократных измерений времен релаксации составляют 2–3 % отн., амплитуд спин-эхо – 1–2 % отн. и могут быть снижены в (n)1/2 раз путем n накоплений амплитуд сигналов спин-эхо ЯМР. По показателю чувствительности К = ν2D2 [106⋅Гц2м2] = 2285 Мгц2см3 релаксометр [3] близок к зарубежному аналогу – «Minispec pc120» (Bruker). Измерения времен спин-решеточной релаксации T1i и населенностей протонов Р1i выполнялись последовательностью импульсов 90-t-90°-τ0-180° по методике Хана [6], а спин-спиновой релаксации T2i и населенностей протонов Р2i – по методике Карра–Парселла–Мейбум-Гилла (КПМГ) [7] последовательностью импульсов 90-t-(180°-2t-)N.

Зависимости огибающей амплитуд Ае спин-эхо при измерениях T1i и T2i по методикам Хана и КПМГ после амплитудного детектирования описывались уравнениями:

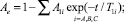
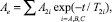(1)

где А0i в относительных единицах соответствует относительному доле протонов фазводы разной степени кристаллизации а T1,2i – временам спин-решеточной и спин-спиновой релаксации этих протонных фаз i = А, В. Использовано устройство безградиентного термостатирования образца в датчике ЯМР [2] с низким уровнем электромагнитных шумов. Градиент температур не превышает 0,2 град./см в диапазоне от –15 до + 200 °C.

Для вычисления энергий активации ЕА определялись прямолинейные участки Т1 и Т2 от обратной температуры 103/Т∙К в прикладной программе Advanced Grafer. При Аррениусовом характере зависимости времен корреляции tс = tоехр(ЕА/RT) (где tо предэкспоненциальный множитель, R = 8,314 Дж/моль – универсальная газовая постоянная) в условиях приближения wоtс << 1, ЕА можно определить из времен релаксаци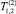и и 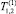измеряемых при температурах T(1) и T(2) по формуле [1]:

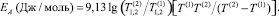(2)

Ошибка определения ЕА есть сумма ошибок измерений T1,2i и T и равна ±5 %.

Результаты калориметрических измерений – термограмма СаCl2⋅6H2O и зависимость напряжения U на электродах термоэлемента приведены на рис. 2. Для остальных ФМВ эндо- и экзотермические эффекты менее выражены.

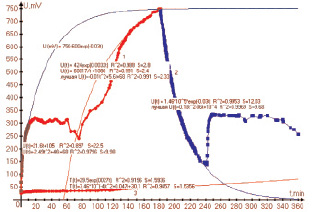
Рис. 2. Зависимость напряжения U (кривая 1, 2) на электродах термоэлемента термограмма СаCl2×6H2O в процессе нагрева и охлаждения в течение 6 часов и температура (3)

Как известно, состояние системы описывается внутренней энергией U, энтальпией Н = U + PV, (где P и V – давление и объем), энтропией S = klnW, (где kиW – постоянная Больцмана и число возможных микросостояний). Тепловой энергетический эффект возникает за счет изменения U или Н. С уменьшением числа молекул воды в кристаллогидрате U, Н и S уменьшаются. На кривых кристаллизации это проявляется в уменьшении площади экзотермического пика. Наши исследования показали, что наиболее выраженный экзотермический эффект и соответственно прирост напряжения ∆U = 250–350 mV на термоэлементе (ТЭ) наблюдается для СаСl2⋅6H2O при температуре образца Тс » 21 °С.

Выявлению тонкостей ФП посвящено исследование методом ЯМР-релаксометрии.

Результаты измерений зависимостей времен спин-решеточной Т1А, Т1В и спин-спиновой Т2А, Т2В релаксации от обратной температуры 103/Т для СаСl2⋅6H2O приведены на рис. 3, временные зависимости времен релаксации в CaCl2⋅6H2O в области ФП при температурах 18–26 °С – на рис. 4. В скорость (Т1,2)–1 релаксации протонов воды дают два вклада: внутримолекулярный 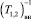, характеризующий релаксацию от вращения молекул гидратированной воды и межмолекулярный 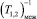, от трансляционной подвижности воды в расплаве [1]:

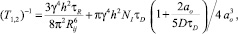(3)

где g/2p = 4256/с⋅гс – гиромагнитное отношение протонов; h = 6,626⋅10–34 Дж/с – постоянная Планка; NI = 6,75⋅1028 м–3 – число спинов в см3; ao = 1,38⋅10–10 м – средний диаметр молекулы воды; Rij = 1,52⋅10–10 м – среднее расстояние между протонами, τR = 2,7⋅10–12 с и tD = a2o/12D – времена корреляции вращательного и трансляционного движений, D = 1,85⋅10–9 м2/с – коэффициент самодиффузии молекул воды.

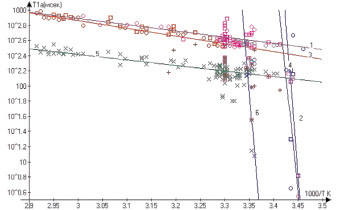
Рис. 3. Температурные зависимости времен релаксации в CaCl2⋅6H2O. Кривые 1, 2 (круги) – Т1А, кривые 3,4 (квадраты) – Т2А, кривые 5, 6 (крестики) – Т2В

Как механизм релаксации следует рассматривать модуляцию диполь-дипольных взаимодействий, вызванных реорентационными движениями протонов воды, связанных водородными Н-связями и в ур. (3) можно учитывать только внутримолекулярный вклад.

Для CaCl2⋅6H2O наблюдается два времени спин-решеточной Т1А, Т1В и спин-спиновой Т2А, Т2В релаксации, отнесенные нами соответственно к свободно ориентирующейся воде в жидкой фазе и фазе с определенной степенью ассоциативности кластеров воды. Более длинные времена релаксации Т1А и Т2А на рис. 3 отнесены к протонам воды в незакристаллизованной протонной фазе, а Т1В, Т2В – к протонной фазе с элементами упорядоченности. Как видно, ФП сопровождается разбросом времен релаксации ∆Т2 » 400–1000 мс в диапазоне температур 103/Т » 3,3–3,35 (27–25 °С). Температурные зависимости Т1А, Т2А и Т2В от 1000/Т К характеризуются экспонентами, что позволяет рассчитать энергии активации ЕА молекулярного движения в высокотемпературном 103/Т = 2,9–3,42 (19–72 °С) и низкотемпературном интервалах 103/Т = 3,42–3,45 (17–19 °С). При 103/Т = 3,42 (19 °С) на зависимости Т1А наблюдается резкий излом с изменением крутизны наклона, т.е. с изменением ЕА.

Две протонных фазы в кристаллогидрате CaCl2⋅6H2O не является чем-то необычным – двухкомпонентность наблюдается даже в чистой воде [7, с. 114]. В ней также имеется различие в значениях ЕА в разных температурных диапазонах, правда, не такое разительное, как в нашем случае. Для 19–72 °С ЕА для воды и ЕА полученная нами для CaCl2⋅6H2O весьма близки – 3,7 и 3,79 ккал/моль соответственно.

Временные зависимости времен релаксации в CaCl2⋅6H2O на рис. 4 при ФП (18–26 °С, 103/Т К = 3,35–3,44) носит сложный характер. По обеим протонным фазам А и В времена релаксации меняются в колебательном режиме. Так, на кривой 1 – Т2А и 2 – Т2В в зависимости видно несколько минимумов, что можно интерпретировать, согласно ур. (3), как несколько зон упорядочения (укорочения Т2А и Т2В). Процесс идет путем многоэтапного упорядочения (промежуточной кристаллизации) с последующим плавлением (локального роста Т2) и заканчивается при конечном падении до Т2А = 4 мс в результате полной кристаллизации. Процесс можно назвать структурно-динамическим фазовым переходом (СДФП). Снижение Т2А и Т2В при СДФП возникает по формуле (4) при уменьшении межпротонного расстояния Rij в результате упорядочения молекул воды и сопровождается выделением тепла. Термограмма на рис. 3 явственно демонстрируют это. Амплитуда сигнала ЯМР Ао, характеризующая в основном длинновременную компоненту (кривая 3), на рис. 4 демонстрирует падение в ходе остывания CaCl2⋅6H2O.

Как это отмечено в работе [5], при охлаждении происходит наложение множественных структурных и фазовых переходов. Центры кристаллизации агрегативно неустойчивы, и в ходе охлаждения в них происходит рост дисперсной фазы за счет молекул, задержавшихся в дисперсионной среде из-за вязкости. Сам процесс перехода жидкой фазы в кристалл можно характеризовать уравнением Колмогорова–Аврами:

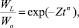(4)

где WL и Wo – веса жидкой и кристаллизованных фаз на момент t; Z – константа скорости кристаллизации Z = πNG3ρs/3ρl; n – Avramiindex; N = Noexp (–ED/kT – ∆U*/kT) – скорость формирования зародышей кристаллизации; ED – энергия активации перехода молекул через поверхность «жидкость-зародыш», ∆U* – свободная энергия формирования зародышей, G = exp(–C/T – D/T∆Tm) – скорость роста кристалла; C, D – константы; ∆T – температура переохлаждения, m – индекс, характеризующий вторичное зародышеобразование, ρs и ρl – плотности твердой и жидкой фаз. При n = 3–4 идет трехмерный рост кристаллов, при n = 2 образуются фибриллы, при n = 1 – одномерные дендриты.

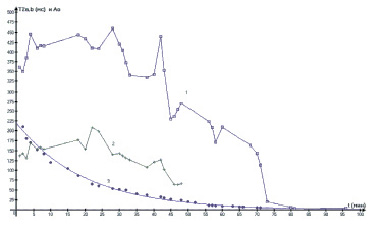
Рис. 4. Временные зависимости времен релаксации в CaCl2⋅6H2O во временном интервале фазового перехода 18–26 °С в процессе охлаждения. Кривая 1 (квадраты) – Т2А, кривая 2 (крестики) – Т2В, кривая 3 (черные) – Ао

В случае CaCl2⋅6H2O снижение концентрации незакристаллизовавшейся фазы может характеризоваться амплитудой сигнала ЯМР Ао и его можно описать уравнением типа ур (4). Аппроксимация Ао с коэффициентом R2 = 0,991 и S = 5,5 описывается уравнением

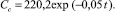(5)

На кривых 3, 4 (рис. 3) и 1, 2 на рис. 4 резкие изменения Т2А и Т2В, в несколько раз превышающие ошибку эксперимента, не могут быть отнесены к ФП II, поскольку наблюдается экзотермический эффект. Их нельзя также приписать ФП I первого рода, поскольку пока еще нет изменения агрегатного состояния. Мы относим их к СДФП как процесс формирования упорядоченных сверхструктур (СС) с последующим их разрушением для формирования структуры с более высокой степенью упорядочения. СДФП ведет к колебаниям Rij (снижению при образовании СС и росту при их разрушении), что ведет к колебаниям Т2А и Т2В в соответствии с ур (3). Формирование СС есть демонстрация стремления открытых систем к минимуму свободной энергии U и энтропии S. В нашем случае кристаллизация CaCl2⋅6H2O – самопроизвольный процесс и изобарно-изохорный потенциал (энергии Гиббса G) определяется большим уменьшением энтальпии ∆H, чем энтропийного фактора T∆S (∆H < 0, T∆S < 0, |∆H| > |T∆S|), что дает отрицательное ЕАSD:

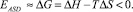(6)

Полученные результаты позволяют осуществить надлежащий подбор рабочих веществ с разными температурами ФП и создать круглосуточный термоэлектрический генератор (ТЭГ) напряжения и тока. Даже при температуре окружающей среды равной 22,1 °С, напряжение на батарее ТЭ равно 13,56 В.

Выводы

1. Для CaCl2⋅6H2O на термограммах наблюдался выраженный экзотермический эффект и двухэкспоненциальная огибающая амплитуда сигналов спин-эхо ЯМР.

2. На температурных зависимостях времен релаксации проявляются резкие изменения, связываемые нами со структурно-динамическими фазовыми переходами (СДФП), возникающими в результате образования и последующего разрушения сверхструктур с возрастающей степенью упорядочения по мере остывания образца.

3. Зависимости релаксации демонстрируют сложный, многоэтапный процесс с изменениями времен релаксации и межпротонных расстояний.

4. Предложен макет круглосуточного автономного термоэлектрического генератора.

Смоляков Б.П., д.ф.-м.н., профессор, ФГБОУ ВПО «Казанский государственный энергетический университет», г. Казань;

Корнилов В.Ю., д.т.н., профессор, ФГБОУ ВПО «Казанский государственный энергетический университет», г. Казань.

Работа поступила в редакцию 17.10.2013.