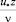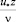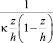Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Строгое математическое описание турбулентного течения, не включающее каких-либо априорных постулатов, гипотез, экспериментальных фактов, до настоящего времени не разработано. За время, прошедшее с работы О. Рейнольдса [10], в которой впервые движение водной массы было разделено на «среднее» и «относительное молярное» движение и указано на аналогию между «относительным молярным движением» и тепловым движением молекул, впоследствии сформировалось научное направление статистической гидромеханики. Усилия ученых, работающих в рамках этого направления, были сосредоточены на получении количественных соотношений между характеристиками этого «относительного молярного движения», которое стало называться турбулентностью. Использование статистических методов исследования турбулентности было объективно необходимым, особенно на первых порах, когда сведения о структуре турбулентности были крайне скудными, и эти «относительные молярные» движения представлялись случайными и хаотическими. На основе статистических подходов явление исследуется как некоторая «данность», при этом не рассматривается причинно-следственные связи между различными факторами, определяющими возникновение и развитие рассматриваемых явлений.

Предпринимаемые в течение двух столетий отчаянные попытки ведущих ученых мирового уровня создать теорию турбулентности в форме замкнутой системы уравнений, не увенчавшиеся успехом, заставляют задуматься о том, не является ли этот статистический подход к решению проблемы тупиковым. Малая результативность этого подхода привела к необходимости разработки подходов феноменологических, представляющих собой комбинацию некоторых теоретических представлений и опытных данных. К настоящему времени среди таких подходов наибольшую популярность приобрела полуэмпирическая теория Л. Прандтля, предложенная им в 1926 году [8], в которой рассматривается процесс переноса импульса силы трения между слоями турбулентного потока.

Простота и наглядность этой модели, восходящей по своей сути к кинетической теории газов, а также ее результативность, обусловили ее широкую известность. Она включена в состав практически всех курсов гидромеханики и гидравлики. Однако эта модель основана на ряде допущений, содержащих ту или иную степень риска.

Предполагается, что при турбулентном движении касательные силы между слоями возникают вследствие обмена количеством движения между слоями при пренебрежимо малом влиянии физической вязкости.

Величина касательных напряжений связывается только с компонентами турбулентных пульсаций скорост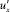и и 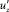в виде уравнения Лоренца:

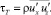(1)

Мгновенное значение продольной пульсационной составляющей скорости 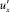связывается с градиентом осредненной скорости соотношением:

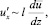(2)

где l – неопределенный параметр с размерностью длины, названный Л. Прандтлем по аналогии с длиной свободного пробега молекул длиной пути перемешивания.

Первая часть выражения (2), характеризующая приращение осреднённой продольной скорости на длине l, является точным только на малых (строго на бесконечно малых) l, когда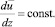

Более поздние исследования турбулентности показали, что турбулентный обмен в водном потоке происходит в широком диапазоне масштабов пульсаций, и выделить какой-либо масштаб не представляется возможным (хотя в последнее время формируется представление о том, что основная доля переноса приходится на крупномасштабные (когерентные) структуры) [9], соизмеримые с поперечными размерами потока.

В теории Л. Прандтля предполагается, что длина пути перемешивания l возрастает с расстоянием от жесткой поверхности трения, при этом постулируется линейность изменения l:

l = κz, (3)

где κ – неопределенный коэффициент пропорциональности.

Вертикальная пульсационная составляющая скорости 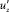считается зависящей от тех же факторов, что и 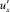, и по порядку величины, близкой к :

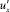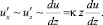(4)

Однако выполнение измерения интенсивности турбулентности показывают, что характер изменения 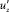по координате z качественно отличается от характера изменения 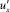, кроме того, 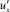по абсолютной величине в 2,3–3 раза превосходит .

Выразив таким образом значения, и через осредненные величины можно получить следующее уравнение:

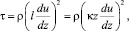(5)

которое называют уравнением Л. Прандтля. Эффект операции осреднения, которая предусматривается уравнением (1), заменяется операцией с осредненными по времени скоростями, что допустимо только при условии тесной корреляции между пульсациями скорости.

При интегрировании уравнения (5) касательное напряжение в потоке τ принимается постоянным и равным касательному напряжению на стенке:

τ = const = τ0. (6)

Последнее предположение является достаточно грубым, противоречащим уравнению равновесия сил, действующих в равномерном потоке, или, иначе, основному уравнению равномерного движения, которое для плоского потока записывается в виде:

τ = ρghi, (7)

где h – глубина потока над границей трения; i – гидравлический уклон.

Эти предположения позволили достаточно просто проинтегрировать уравнение (5) и получить известный логарифмический профиль скорости Прандтля:

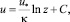(8)

где 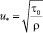 – динамическая скорость.

Рискованность сделанных предположений не позволяли Л. Прандтлю надеяться на успех его теоретических построений, поэтому, когда опыты И. Никурадзе [7, 16] подтвердили справедливость профиля (8) для всего потока как в гладких, так и в шероховатых трубах, сам Л. Прандтль назвал это «не более чем счастливой случайностью». Произошедшая затем «канонизация» логарифмического профиля скорости привела к тому, что отмеченные выше интимные подробности его происхождения стали забываться, а скромная оценка его универсальности, данная самим Л. Прандтлем, не упоминается вовсе. На это указывал, в частности, профессор В.Н. Гончаров [4]: «Часто встречающееся утверждение о полном и точном совпадении этих спорных решений и о полном подтверждении, в силу этого, бесспорности теоретической базы этих решений не отвечает действительности».

Представленное на рис. 1 и 2 сопоставление с данными измерений И. Никурадзе известных логарифмических профилей:

– для гладких труб:

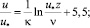(9)

– для шероховатых труб:

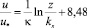(10)

обнаруживает возрастающее расхождение между измеренными скоростями и логарифмическими профилями, которые отвечают измерениям лишь у стенки в слое толщиной около 0,15 от радиуса трубы r. (На это обстоятельство было впервые указано К. Милликеном [15]).

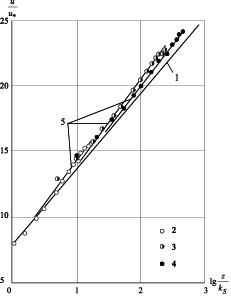
Рис. 1. 1 – профиль И. Никурадзе; 2–4 – данные И. Никурадзе (2 – Re = 108∙103; r/kS = 15; 3 – Re = 344∙103; r/kS = 252; 4 – Re = 970∙103; r/kS = 507); 5 – расчет по (10) с поправкой (19)

Возникает предположение, что отмеченное расхождение связано с тем, что при выводе логарифмического профиля Л. Прандтль не учел изменение касательного напряжения с расстоянием от стенки, что само по себе вызывает удивление. Сохраняя гипотезу Л. Прандтля относительно длины пути перемешивания (l = κz) и учитывая изменения τ, получаем соотношение:

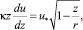(11)

интегрирование которого дает следующий вид профиля скорости:

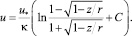(12)

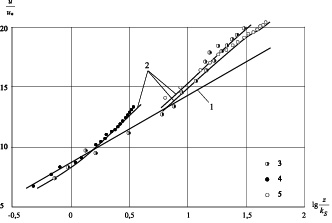
Рис. 2. 1 – расчет по соотношению (10) при = 0,4 и uκ/u* = 8,48; 2 – расчет по соотношению (10) c поправкой (19); 3 – данные С. Коррсина и А. Кистлера, δ/kS = 30 (гофрированная поверхность); 4 – данные В.С. Боровкова, h/kS = 4 (цилиндрические выступы, расположенные в шахматном порядке); 5 – то же, h/kS = 50 (деревянный канал)

Находя постоянную интегрирования С из условия 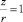и u = umax, получаем следующий профиль в форме закона избыточной скорости:

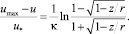(13)

Вид профиля (13) показан на рис. 3.

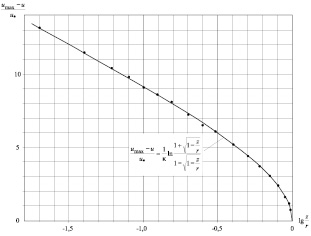
Рис. 3. Профиль с учетом изменения t

Сопоставление полученного профиля, учитывающего изменение τ, с данными измерений И. Никурадзе показывает на неприемлемо большие расхождения расчетных и экспериментальных данных, которые не могут быть исключены корректировкой величины κ. По всей вероятности, именно это обстоятельство явилось причиной того, что Л. Прандтль предпочел не учитывать изменение касательного напряжения с расстоянием от твердой границы.

Поскольку профиль скорости Л. Прандтля дает явно лучшую сходимость с экспериментом, чем профиль (13), профессором А.А. Саткевичем [11] был предложен способ учета изменения τ в уравнении переноса с одновременным изменением гипотезы относительно длины пути перемешивания в виде:

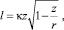(14)

принятом на основе анализа экспериментальных данных. Хотя выражение (14) лишь до некоторой степени согласуется с экспериментальными данными И. Никурадзе (рис. 4), предложенный прием позволяет учесть изменение τ при сохранении неизменным профиля Л. Прандтля. Действительно, уравнение переноса при этом запишется в виде:

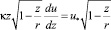(15)

и приводится к уравнению, проинтегрированному Л. Прандтлем.

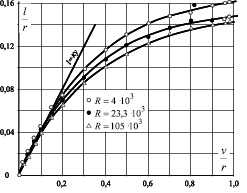
Рис. 4. l/r в функции от v/r для малых чисел Рейнольдса по опытам И. Никурадзе (гладкие трубы)

Если принять для l выражение в виде [1]:

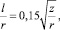(16)

можно получить более сложный профиль скорости:

(17)

дающий ненулевые значения скорости у твердой границы потока, близкие к данным измерений И. Никурадзе в точке, ближайшей к твёрдой границе потока.

Поскольку «базовые» профили (9) и (10) согласуются с данными измерений, строго говоря, только вблизи стенки, для описания течения при решении практических задач на больших расстояниях z часто используют «закон следа» в виде логарифмического профиля с аддитивной добавкой, которая представляется обычно в виде графика

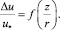
Максимальное значение добавки (на оси трубы) близко к 1, для течения в пограничном слое на его внешней границе добавка близка к 2,5 [1]. Без учета этой поправки погрешность логарифмического профиля в трубе может достигать 5–6 %, а в пограничном слое 12–15 %. Эти расхождения вызвали значительную активность в разработке альтернативных подходов к уточнению распределения скоростей при турбулентном течении в трубах и открытых потоках.

Можно указать на индуктивную теорию Г. Рейхардта, модель переноса завихренности К. Тейлора, теорию Дж. Ротта, обзор которых приведен в [11], а также ряд предложений, основанных на подходе Буссинеска при уточненном описании турбулентной вязкости νT. Достаточно эффективным оказалось использование следующего выражения, аппроксимирующего данные многих измерений [2]

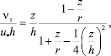(18)

с помощью которого удалось получить следующие поправочные функции к логарифмическим профилям:

– для течения в трубах

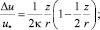(19)

– для течения в каналах

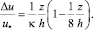(20)

Сопоставление профилей (9) и (10), включающих поправочные функции (19) и (20) с данными измерений в каналах и трубах, приведенное на рис. 1 и 2, указывает на хорошую сходимость с данными измерений. Как показано в [2], такая коррекция профилей скорости соответствует также и хорошо известным экспериментальным законам сопротивления.

Следует при этом отметить, что такие подходы в основе своей являются эмпирическим, и зависимости (19) и (20) содержат неопределенный параметр κ и, главное, не находит каких-либо ясных физических объяснений.

Попытка обосновать более стройную концепцию течения была сделана Т. Карманом [13], которая основана на предложенной им гипотезе подобия местного течения. Смысл гипотезы состоит в том, что если картина течения между близкими слоями потоками 1 и 2 обусловлена исключительно местными обстоятельствами, то это требует некоторой закономерной пропорциональности между факторами, определяющими ход кривой распределения скоростей в окрестности рассматриваемых слоёв. Представляя скорость в слое 1 и 2 в виде разложений Тейлора:

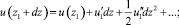(21)

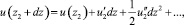(22)

с учетом сформулированной гипотезы локального подобия Т. Карман предполагает:

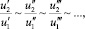(23)

откуда следует, что

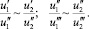(24)

Рассматривая только первое из этих соотношений и учитывая фактор размерности, можно записать:

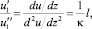(25)

где l – некоторый линейный масштаб и κ – коэффициент пропорциональности. Принимая во внимание изменение τ, Т. Карман получает следующий профиль скорости:

(26)

в котором неопределенным остается только величина κ. Сопоставлением профиля (26) с опытными данными Денха и И. Никурадзе найдено значение κ = 0,36

Следует отметить, что основная гипотеза Т. Кармана о локальном подобии течения с современной точки зрения открыта для критики, поскольку обмен количеством движения между соседними слоями осуществляется пульсациями скорости различных геометрических масштабов, в том числе и на тех, которые соизмеримы с размером потока. Хотя длина l в теории Т. Кармана не имеет физического смысла длины смещения, а является лишь масштабом локального подобия течения, из этого следует, что по своей сущности она должна быть величиной малой по сравнению с размером потока. Эти обстоятельства противоречат друг другу и не укладываются в логику локального подобия течения. Теория Т. Кармана, более формальная по сравнению с физически более прозрачной теорией Л. Прандтля, обладает схожими недостатками: неопределимостью масштабной длины l и отсутствием другой возможности определить параметр κ, кроме экспериментальной.

Следуя Л. Прандтлю, рассмотрим вертикальный перенос количества движения от одного слоя к другому (рис. 5) через единичную площадку, расположенную на расстоянии z от стенки и движущуюся с осредненной местной скоростью .

Выбор подвижной площадки связан с тем, что рассматривается количество движения в выделенном слое над площадкой и под нею.

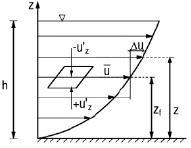
Рис. 5

Как и в схеме Л. Прандтля, будем считать, что вертикальный перенос количества движения осуществляется пульсациями скорости 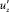, интенсивность которых и вертикальный масштаб l22 в различные моменты времени различен, что не нашло отражения в теории Л. Прандтля. Обычно пульсация скорости представляется процессом полигармоническим со случайно изменяющимися амплитудами каждой гармоники. Такое представление предполагает, что в каждый момент времени жидкая частица участвует одновременно в нескольких разномасштабных движениях (рис. 6).

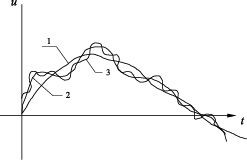
Рис. 6. 1 – крупномасштабные пульсации; 2 – пульсации среднего масштаба; 3 – пульсации малого масштаба

В большинстве случаев мелкомасштабные движения как бы «вложены» в крупномасштабные, хотя могут существовать и независимо от крупномасштабных. Эти пульсации согласно данным спектральных измерений вертикальных пульсаций [5] переносят не более 1 % энергии турбулентности и могут не учитываться.

С учетом этого выделим из общего спектра пульсаций 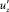лишь те пульсации, при прохождении которых изменяется направление движения через рассматриваемую площадку. Таким образом, дальнейшее рассмотрение ограничим крупномасштабными турбулентными образованиями, размеры которых будут сравнимы с наибольшими длинами соответствующих им автокорреляций.

В координатной системе, движущейся с осредненной средней скоростью, рассматриваемое время действия пульсаций того или иного знака определяется ее линейным масштабом и пульсационной скоростью.

Очевидно, что время действия пульсаций одного знака и соответствующий ему линейный масштаб будут случайно изменяющимися величинами, к анализу которых можно применить вероятностные методы и уже разработанные статистические приемы.

Время действия пульсации одного знака будет зависеть также и от способа их регистрации. Если регистрирующий прибор неподвижен, то время действия пульсаций будет определяться осредненной местной скоростью u и продольным пространственным масштабом этих пульсаций.

Поскольку вертикальный обмен импульсом в турбулентном потоке рассматриваем в подвижной координатной системе, а большинство измерений сделано неподвижными приборами, целесообразно рассматривать соотношения между характеристиками турбулентности в неподвижной и движущейся системе координат.

Так, для продольной пульсации в неподвижной системе координат период действия t11f равен:

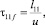(27)

где l11 – продольный масштаб продольных пульсаций; u – осредненная по времени местная скорость.

Аналогично для вертикальных пульсаций период их действия t21f в неподвижной системе координат:

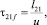(28)

где l21 – продольный масштаб вертикальных пульсаций.

При этом пространственные масштабы турбулентности находятся в простом соотношении с соответствующими масштабами времени:

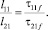(29)

При измерениях турбулентности приборами, движущимися с местной скоростью u, периоды действия пульсаций будут равны:

– для продольных пульсаций:

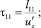(30)

– для вертикальных пульсаций:

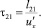(31)

Хотя, периоды действия пульсаций в подвижной системе координат увеличились, поскольку 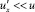их соотношение остается неизменным:

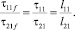(32)

Данные измерений [2] показывают, что отношение 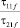зависит от коэффициента гидравлического сопротивления и при средних его значениях близко к 10, при этом продольный масштаб вертикальных пульсаций l21 близок к глубине потока h.

В схеме вертикального обмена Л. Прандтля рассматривается вертикальный перенос количества движения, поэтому представляет интерес оценка вертикального пространственного масштаба l22 вертикальных пульсаций скорости 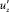и соответствующего периода их действия в подвижной системе координат:

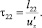(33)

Соотношение между масштабами l21 и l22 зависит от анизотропии турбулентности. Так, для изотропной турбулентности 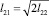, для сдвиговых течений 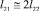[6].

Учитывая, что стандарт пульсаций 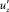близок к динамической скорости u* и продольный масштаб l22 близок к h, время действия вертикальных пульсаций составит:

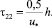(34)

Что можно представить в виде безразмерного комплекса – динамического числа Струхаля:

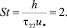
Таким образом, рассматривая вертикальный перенос количества движения между слоями потока с использованием схемы Л. Прандтля, следует учитывать вертикальный масштаб l22 вертикальных пульсаций и время их действия (34) в общем времени обменного цикла.

Очевидно, что уточнение расчетной схемы Л. Прандтля на данном этапе состоит в четкой физической трактовке величины l в соотношении (2), которая принимается адекватной вертикальному масштабу турбулентных пульсаций скорости l22.

Следует отметить, что вследствие трехмерности турбулентного течения появление продольной пульсации 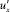, по всей видимости, связано не только с обменом количеством движения по вертикали, что находит отражение в существенно неодинаковом времени действия пульсаци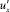й и 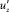и в достаточно слабой коррелированности этих пульсаций.

Как отмечалось выше, изменение количества движения в граничащих слоях потока вследствие вертикального обмена в единицу времени считается эквивалентом действия мгновенного касательного напряжения ta на единичной площади граничной поверхности:

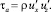
Осреднение по времени соотношения данного выражения дает известное уравнение Лоренца (1):

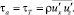
Это уравнение, а также ряд дополнительных предположений, составляют основу полуэмпирической теории Л. Прандтля. Рассмотрим их более подробно в свете имеющихся данных о турбулентности сдвиговых течений.

Ключевое предположение Л. Прандтля (2), связывающее продольную пульсацию скорости 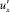с градиентом осредненной скорости 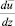и длиной пути перемешивания l, т.е. с осредненными по времени величинами является внутренне противоречивым. Очевидно, что продольная пульсация скорости, далее используемая Л. Прандтлем в уравнении Лоренца и подвергающаяся последующему осреднению по времени в произведении с вертикальной пульсацией, является величиной мгновенной (актуальной). В то же время и 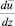и величина l являются величинами постоянными, не изменяющимися во времени.

Поскольку при исследованиях турбулентности пульсационные скорости определяются в форме так называемых «стандартов» пульсаций – среднеквадратичных отклонений от скорости , то в дальнейшем анализе они могут быть использованы совместно с коэффициентом взаимной корреляции Rxz , который равен

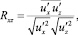(35)

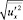где и 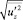 – стандарт продольной и вертикальной пульсации скорости соответственно.

Сопоставление этого выражения с уравнением Лоренца показывает, что числитель выражения (35) представляет собой , что позволяет записать следующее уравнение:

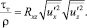(36)

Уравнение (36) может быть использовано для проверки взаимной согласованности характеристик турбулентности, полученных экспериментально.

Анализ многочисленных опытных данных различных авторов позволил получить следующие зависимости [14] для стандартов продольных и вертикальных пульсаций скорости:

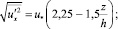(37)

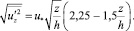(38)

Опытные данные по измерениям коэффициентов корреляции представлены на рис. 7

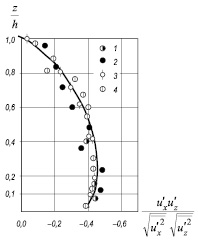
Рис. 7. Изменение коэффициента корреляции по глубине потока: 1, 2 – данные В.С. Боровкова (1 – i = 0,072; 2 – i = 0,232); 3 – данные Дж. Лауфера, прямоугольный напорный канал; 4 – данные Ж. Конт-Белло, прямоугольный канал

При использовании уравнения (36) для проверки взаимной согласованности данных измерений турбулентности необходимо уточнить предположение о величине и характере изменения турбулентного напряжения tт по глубине потока. Наиболее простым является предположение tт = const = t0, как известно принятое Л. Прандтлем, позволяющее записать следующее выражение для коэффициента корреляции:

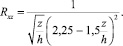(39)

Расчетные значения для различных , полученные по зависимости (39), приведены в табл. 1.

Данные по величине Rxz1, полученные в предположении tт = const = t0, обнаруживают значительные расхождения с данными измерений, приведенными на рис. 7, и нереальные значения корреляции в придонной зоне и у поверхности потока. В связи с этим расчет Rxz был выполнен с учетом изменения τ по глубине потока в виде:

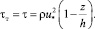(40)

Таблица 1

Расчет взаимной корреляции продольных и вертикальных пульсаций скорости при t = const и с учетом изменения t по глубине потока

При этом выражение для коэффициента корреляции приобретает вид:

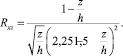(41)

Расчетные значения Rxz2 приведенные в табл. 2, хотя и обнаруживают нереальные значения Rxz2 непосредственно у дна, в остальной части потока качественно согласуются с данными измерений корреляции (см. рис. 7). Нереально высокие значения коэффициента корреляции в придонной области могут быть вызваны рядом причин:

– возможной неточностью зависимостей (38) и (39);

– возможностью внедрения в зону вязкого подслоя при малых , где течение имеет перемежающийся характер (ламинарно-турбулентный);

– влиянием вязкой составляющей трения, которая в выполненном анализе не учитывалась.

Для того чтобы оценить возможность внедрения в зону вязкого подслоя, необходимо преобразовать координату в безразмерную координату 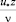, по которой принято определять толщину вязкого подслоя. Выполним такое преобразование для условий течения в гладких границах с использованием формулы Блазиуса:

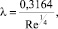(42)

которая может быть преобразована к следующему виду, удобному для анализа:

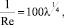(43)

где 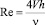 – число Рейнольдса.

При этом преобразование координат запишется в виде следующего алгоритма:

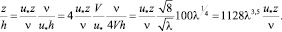(44)

Из выражения (44) следует, что преобразование весьма сильно зависит от коэффициента λ. Сопоставление координат и 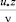, выполненное для различных значений λ, приведено в табл. 2.

Данные табл. 3 показывают, что в условиях гладких границ потока вязкий подслой, который обычно связывают с координатой 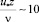, в зависимости от величины λ может занимать значительную часть потока от 0,02h до 0,3h, что следует учитывать при анализе и использовании экспериментальных данных. Нереальные значения Rxz для придонной зоны (табл. 1) связаны с тем, что зависимости (38) и (39) неравномерно применялись для зоны вязкого подслоя. Рассмотрим далее возможность влияния вязкой составляющей трения на оценку величины Rxz , записывая полное напряжение трения в виде суммы турбулентной и вязкой составляющей:

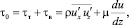(45)

где μ = ρν – динамическая вязкость.

Для получения количественных оценок градиента скорости примем его в форме, восходящей к логарифмическому профилю скорости (8), дифференцируя который запишем:

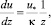(46)

где κ – параметр Кармана, близкий к 0,4.

Таблица 2

Расчет 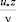при различных значениях l

Выражая tт из (45) с подстановкой соотношения (46) и учетом линейного изменения касательного напряжения, получаем:

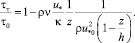(47)

Это выражение для потока в гладких границах с использованием (43) можно преобразовать к виду:

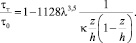(48)

Рассчитанные по зависимости (48) значения для придонной зоны потока при двух значениях λ приведены в табл. 3.

Результаты расчета (табл. 3) показывают, что вязкая составляющая трения в пристенной зоне сильно зависит от λ и с увеличением сопротивления может оставаться существенной на больших расстояниях от верхней границы вязкого подслоя. Близкие результаты были получены Ю.В. Брянской [3].

Таблица 3

Расчет при различных значениях l

Использование полученных результатов позволяет уточнить оценки корреляции Rxz в придонной зоне потока за счет более точного определения tт (табл. 3).

Результат расчета обнаруживает достаточно близкое соответствие расчетных значений Rxz с данными измерений (см. рис. 7). Таким образом, результаты измерений стандартов пульсаций скорости и взаимных корреляций обнаруживают приемлемую сходимость и могут считаться в достаточной мере точными.

Определив турбулентную составляющую tт в полном напряжении трения t0, сделаем попытку исследовать поведение длины пути перемешивания l в уравнении Л. Прандтля:

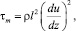(49)

считая логарифмическое распределение скоростей (8) всего лишь достаточно точной аппроксимацией большого массива экспериментальных данных, не принимая при этом во внимание известные гипотезы Л. Прандтля, которые приводят к профилю вида (8).

Принимая 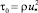из (48) и (49) с использованием (46), получаем:

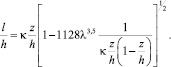(50)

Заметим, что использованный профиль (8) в качестве аппроксимации опытных данных совпадает с ними при κ = 0,4.

Расчет по зависимости (50) приведен в табл. 4.

Таблица 4

Расчет изменения длины пути перемешивания в потоке при разных значениях l

Анализ расчетных данных, приведенных в табл. 4, показывает, что при λ = 0,02–0,03 значения l оказываются близкими к l = 0,4z. Этот результат можно было ожидать, учитывая условия выполненных расчетов. Он также подтверждает высокую точность соотношений, использованных для расчета tт. Данные расчетов показывают также, что с возрастанием λ до 0,04–0,05 величина κ не остается постоянной и несколько снижается.

Завершая рассмотрение вопросов, затронутых в настоящей статье, следует заключить, что полуэмпирическая теория Л. Прандтля содержит внутренне противоречивые предположения, которые должны быть пересмотрены при дальнейших попытках ее модернизации с учетом реальных параметров турбулентности, приведенных в настоящей статье. Результаты экспериментальных исследований турбулентных пульсаций скорости и их взаимных корреляций, а также полученные аппроксимационные зависимости, не противоречат друг другу и согласуются с известными закономерностями изменения турбулентного и вязкого течения по глубине потока.

Боровков В.С., д.т.н., профессор кафедры гидравлики, ФГБОУ ВПО «Московский государственный строительный университет», г. Москва;

Ханов Н.В., д.т.н., профессор кафедры гидравлики, ФГБОУ ВПО «Московский государственный университет природообустройства», г. Москва.

Работа поступила в редакцию 14.10.2013.