В настоящее время для применения в космической и военной технике, а также для научных исследований рельсотроны рассматриваются как перспективные электромагнитные ускорители тел до скоростей, достигающих 10 км/с и более [1, 2, 6]. Поэтому расчет параметров рельсотронов представляется актуальной задачей. Рельсотрон является электромеханической установкой, преобразующей электромагнитную энергию импульса тока в механическую энергию ускоряемого тела и состоящий из двух параллельных шин (рельсов), между которыми движется ускоряемое тело (рис. 1).
Методика расчета
Рассмотрим режим ускорения тела массой m, одиночным импульсом тока i(t) произвольной формы с длительностью τ, амплитудой Im и действующим (среднеквадратичным) значением:
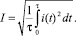 (1)
(1)
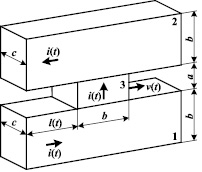
Рис. 1. Принципиальная схема рельсотрона: 1, 2 – одинаковые шины; 3 – ускоряемое тело; v(t) – скорость тела; l(t) – расстояние, пройденное телом в рельсотроне; i(t) – электрический ток; a, b, c, – размеры ускоряемого тела и шин рельсотрона
На основании второго закона Ньютона получаем уравнение движения ускоряемого тела без учета сил сопротивления [5]:
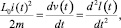
откуда определяем скорость тела:
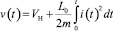 (2)
(2)
и пройденное этим телом расстояние в рельсотроне:
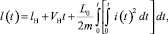 (3)
(3)
причем, с учетом (1, 2, 3) находим при t = τ максимальную скорость тела на выходе из рельсотрона:
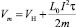 (4)
(4)
и длину рельсотрона:
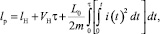 (5)
(5)
где L0 – индуктивность рельсотрона (Гн/м); m = abcρ – масса ускоряемого тела при его удельной плотности ρ (кг/м3); lН = l(0); VН = v(0) – начальное положение тела в рельсотроне и его скорость при t = 0.
При постоянной удельной проводимости материала шин [4]:
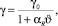 (6)
(6)
усредненной действующей плотности тока δ0 = I/bc и адиабатном нагреве [4] среднее повышение температуры шин над начальной температурой θ0 за время τ составит:
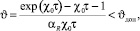 (7)
(7)
тогда
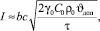 (8)
(8)
где 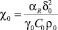 – температурно-временной параметр шин (°С/с); αR – температурный коэффициент проводимости (1/°С); γ0, C0, ρ0 – при температуре θ0 удельная проводимость (1/Ом∙м), удельная теплоемкость (Дж/кг∙°С) и удельная плотность (кг/м3) материала шин соответственно; ϑдоп – допустимое повышение температуры шин над начальной температурой θ0 за время τ.
– температурно-временной параметр шин (°С/с); αR – температурный коэффициент проводимости (1/°С); γ0, C0, ρ0 – при температуре θ0 удельная проводимость (1/Ом∙м), удельная теплоемкость (Дж/кг∙°С) и удельная плотность (кг/м3) материала шин соответственно; ϑдоп – допустимое повышение температуры шин над начальной температурой θ0 за время τ.
Примем, что при импульсе тока i(t) будет существенный поверхностный эффект и механическая прочность шин определяется максимальным механическим напряжением σm при максимальной индукции Bm на поверхности шин [5]:
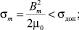
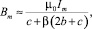 (9)
(9)
причем индуктивность рельсотрона L0 зависит от среднего действующего значения индукции B0 в пространстве между шинами, которая получена, как и индукция Bm, на основе закона полного тока [5]:
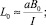
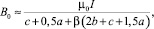 (10)
(10)
где σдоп – допустимое механическое напряжение, которое выдерживает материал шин (Па); β < 1 – безразмерный параметр ослабления индукции вне пространства между шинами; μ0 = 4π∙10–7 (Гн/м) – магнитная проницаемость материала шин и пространства вокруг их.
При a = c; λ = b/a; 1 < λ < 2,5 на основании (9), находим, исходя из механической прочности шин, амплитуду импульса тока Im при параметре β:
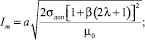
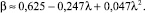 (11)
(11)
Результаты расчета
Для однополярного импульса тока прямоугольной формы (I = Im)
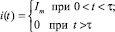 (12)
(12)
при заданных значениях Vm, lp, VH = 0, lH = 0 и размерах рельсотрона a = c на основании (4), (5), (8), (11) получены формулы:
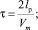
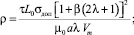
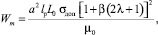 (13)
(13)
причем ширина шин равна:
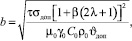 (14)
(14)
где 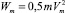 – максимальная кинетическая энергия ускоряемого тела.
– максимальная кинетическая энергия ускоряемого тела.
По формулам (1)–(14) при Vm = (км/с); lp = 9 (м); τ = 2 (мс) проведены расчеты параметров рельсотронов с шинами из особо прочной бериллиевой бронзы [5]: θ0=20 °С; γ0 = 12,5·106 1/Ом·м; αR = 0,0035 1/°С; С0 = 385,5 Дж/°С∙кг; ρ0 = 8230 кг/м3; σдоп = 1350 МПа; ϑдоп = 28,04 °С.
При этом на рис. 2–5 приведены рассчитанные, исходя из механической прочности бериллиевых шин, зависимости параметров рельсотронов от расстояния a между шинами при размерах c = a.
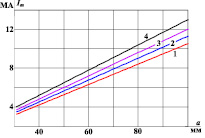
Рис. 2. Зависимости амплитуды импульса тока Im от расстояния a между бериллиевым шинами при размерах c = a: 1 – b/a=1; 2 – b/a = 1,5; Ъ3 – b/a = 2; 4 – b/a = 2,5
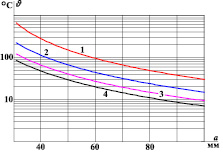
Рис. 3. Зависимости среднего повышения температуры бериллиевых шин ϑ от расстояния a при размерах c = a: 1 – b/a = 1; 2 – b/a = 1,5; 3 – b/a = 2; 4 – b/a = 2,5
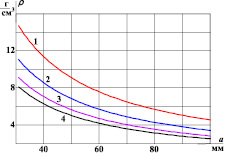
Рис. 4. Зависимости удельной плотности ускоряемого тела ρ от расстояния a при размерах c = a: 1 – b/a = 1; 2 – b/a = 1,5; 3 – b/a = 2; 4 – b/a = 2,5
В таблице приведены результаты расчета по формулам (9)–(11), (14) параметров рельсотронов с бериллиевыми шинами и результаты определения индуктивности L0 рельсотрона на основании энергии магнитного поля по программе компьютерного моделирования Elcut [3] при синусоидальном токе и частоте 50 кГц, когда имеет место существенный поверхностный эффект.
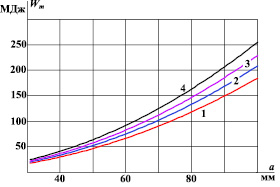
Рис. 5. Зависимости максимальной кинетической энергии ускоряемого тела Wm от расстояния a при размерах c = a: 1 – b/a = 1; 2 – b/a = 1,5; 3 – b/a = 2; 4 – b/a = 2,5
Параметры рельсотронов при I = Im; ϑдоп=28,04 °С и размерах a = c
|
Расчет |
Elcut |
|||||
|
λ = b/a |
β |
b |
a |
Bm/B0 |
L0 |
L0 |
|
– |
– |
мм |
мм |
– |
мкГн/м |
мГн/м |
|
1 |
0,425 |
100,000 |
100,000 |
1,500 |
0,368 |
0,351 |
|
1,5 |
0,360 |
107,297 |
71,532 |
1,426 |
0,361 |
0,354 |
|
2 |
0,319 |
114,067 |
57,033 |
1,377 |
0,352 |
0,339 |
|
2,5 |
0,301 |
123,407 |
49,363 |
1,339 |
0,334 |
0,340 |
Заключение
1. Предложена методика расчета параметров рельсотронов при импульсных токах различной формы и длительности, позволяющая определять возможности рельсотронов, исходя из механической прочности шин.
2. Для однополярного импульса тока прямоугольной формы, при заданной максимальной скорости тела и известной длине рельсотрона, получены формулы для расчета длительности импульса тока, объемной плотности материала ускоряемого тела и его максимальной кинетической энергии. При механической прочности бериллиевых шин результаты расчета амплитуды импульса тока, средней температуры шин при их адиабатном нагреве, объемной плотности ускоряемого тела и его максимальной кинетической энергии приведены в виде графиков зависимостей от расстояния между шинами, которая равна их высоте при разной ширине шин.
3. С увеличением расстояния между шинами и ширины шин уменьшаются средняя температура шин и удельная плотность материала ускоряемого тела, при увеличении амплитуды импульса тока и максимальной кинетической энергии ускоряемого тела.
Рецензенты:Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГБОУ ВПО НИ ТПУ, Национальный исследовательский Томский политехнический университет, г. Томск;
Канев Ф.Ю., д.ф.-м.н., ведущий научный сотрудник института оптики атмосферы им. В.Е. Зуева СО РАН, г. Томск.
Работа поступила в редакцию 17.10.2013.



