Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Исторический опыт свидетельствует о том, что важнейшую роль играла и продолжает играть инженерная смекалка, искусство размышления. С помощью каких средств проще и эффективнее достичь поставленной цели – эта важнейшая задача всегда будет опираться на инженерное искусство. Сюда относится синтез несущих конструкций на уровне топологии. Новая идея конструктивного решения объекта может дать больший эффект, чем оптимизация конструкции устоявшейся геометрии по ее параметрам.

Немецкий ученый Роукс сформулировал закон «борьбы элементов» в организме, по которому восприятие воздействий внешних факторов осуществляется минимумом материала. Постоянное функциональное раздражение вызывает усиление действующего органа путем повышения поставки вещества. Отсутствие раздражения позволяет перенести вещество в другие органы, где, напротив, налицо повышение раздражения. Таков процесс «обволакивания» материей силового поля. Этим объясняется способность живых систем адаптироваться к длительным и многократным воздействиям внешних факторов умеренной интенсивности путем как функциональной, так и морфологической перестройки отдельных структур и систем.

Законы структурообразования, вытекающие из принципа стационарного действия, должны прослеживаться как в организации природы, так и в доведенных до совершенства инженерных конструкциях.

Под топологией мы понимаем расположение узлов и способ их соединения между собой для образования геометрически неизменяемой конструкции. Путем варьирования количества узлов и стержней находят оптимальную топологию.

В работе [1] приведены формулировки и доказательства трех теорем о структурных изменениях, показано применение этих теорем к оптимизации топологии шарнирных систем. Эта задача решается в рамках весовой оптимизации, которая лишь в частных случаях удовлетворяет вариационным принципам структурного синтеза [3]. К тому же она принципиально не применима при композиции из разнородных материалов.

Оптимизация топологии шарнирных ферм осуществляется путем перебора стержней решетки, который в конце концов сводится к укреплению наиболее нагруженных узлов [2]. В этом можно усмотреть некоторый аналог упомянутого выше обволакивания материей силового поля в континуальном теле.

В более общей постановке эта задача рассматривается в работе [4]. Поочередно определяется вес конструкции, полученной в результате удаления какого-либо элемента исходной системы, затем элементы располагаются в так называемом векторе дохода в том порядке, в котором они способствовали минимуму веса. При построении этого вектора рассматриваются ограничения на напряжения. К этому моменту число различных ферм может быть большим, и инженер может выбрать ферму с наименьшей стоимостью изготовления или монтажа.

Оптимизация топологии систем, содержащих балочные элементы, носит более сложный характер. Развитие конечноэлементной методики оптимизации топологии решетчатых рам не исключает параллельное использование стержневых и континуальных конечных элементов. Примером может служить работа [5], в которой при синтезе рамы, являющейся составной частью высотного здания, использованы четырехузловые четырехугольные и двухузловые балочные конечные элементы. Однако полученные решения носят пока декларативный характер и далеки от практического воплощения.

Цель исследования – показать возможность получения на основе универсального проектного критерия и современных программных комплексов оптимальной топологии конструкции.

Материалы и методы исследования

Объектом исследования являются однопролетные одноэтажные рамы, несущие постоянную и временные нагрузки. На расход материалов на их возведение превалирующее влияние оказывают изгибающие моменты.

Изгибающие моменты в балочных элементах рамы можно уменьшить двумя способами:

а) введение шарниров по длине элемента;

б) введение стержней, создающих дополнительные опорные точки.

В конкретном случае на топологию рамы накладывают ограничения, связанные с ее функциональным назначением и условием эксплуатации конструкции.

Упомянутый выше вариационный принцип структурного синтеза гласит [2]: потенциальная энергия системы в положении устойчивого равновесия достигает абсолютного минимума по перемещениям в функциональном пространстве, расширенном за счет полей функций конфигурации и(или) модулей упругости материала. В случае однородного линейно-упругого материала это равносильно минимуму потенциальной энергии деформации. Следовательно, проектный критерий должен отражать смысл изложенного вариационного принципа.

Достаточным условием справедливости постановки задачи весовой оптимизации может быть лишь введение энергетического начала в процедуру оптимального проектирования, что следует из двойственности постановки задач на условный экстремум с интегральными связями. Такая постановка совершенно исключена при использовании в конструкции разнородных материалов, и энергетический критерий структурного синтеза приобретает универсальный характер.

Потенциальная энергия деформации для плоской рамы с учетом значимого влияния лишь изгибающих моментов и продольных сил представляется в виде

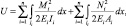(1)

где M – изгибающий момент; N – продольная сила; E – модуль продольной упругости материала; A – площадь поперечного сечения; I – момент инерции сечения; li – длина i-го стержня; n – число стержней.

В случае однородного материала энергетический критерий обеспечивает минимум его расхода. Это становится очевидным при равнонапряженности конструкции по всему объему, что присуще системам из стержней с одноосным напряженным состоянием. В других случаях это достигается варьированием функционала U по параметрам Ai и Ii и соответствующим формированием сечений элементов.

При индустриализации строительства используются стандартные элементы, в том числе прокатные профили, что ограничивает однако доведение до совершенства конфигурации конструкции. Например, площадь сечения A = 26,8 см2 обеспечивается двутавром № 20 (ГОСТ 8239-56) с моментом инерции I = 1840 см4 или двумя швеллерами № 12 (ГОСТ 8240-56) с суммарным моментом инерции 608 см4. Это, безусловно, может нарушить синхронность потенциальной энергии деформации и объема (веса) конструкции, так как в первой характеристике отражаются величины A и I, а во второй – лишь величина A.

Результаты исследования и их обсуждение

Процесс оптимизации топологии рассмотрим на примере однопролетной одноэтажной рамы (рис. 1). Пересечение наклонного стержня со стойкой составляет жесткий узел. Штрихами показан один из вариантов ригеля.

Рассмотрим четыре частных случая представленной топологии (рис. 2). Исключен вариант прямолинейного ригеля с тремя шарнирами, представляющий мнгновенно изменяемую систему.

Численные исследования проводились для рам с пролетами l = 9, 12, 15, 18 м, высотой h = 7,2 м при шаге колонн 4 м. Снеговая нагрузка принята для III снегового района и составила q = 7,2 кН/м. Характеристики материала – стали: объемный вес γ = 7,85∙104 Н/м3, модуль упругости E = 200 ГПа, расчетное сопротивление R = 225 МПа. В расчетах использовался програмный комплекс «ЛИРА 9.4».

Вариант рамы на рис. 2, а представляет собой простейшее решение топологии. Его характеристики даны в табл. 1. При подсчете энергии по формуле (1) интегралы вычислялись по методу прямоугольников.

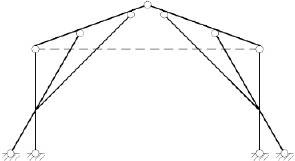
Рис. 1. Плоская рама

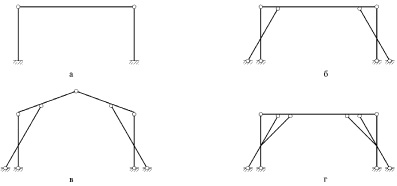
Рис. 2. Варианты топологии рамы

Таблица 1

Характеристики рамы (рис. 2,а)

Заметим, что в качестве доминанты внутренних усилий здесь выступает изгибающий момент в середине ригеля, который оказывает большое влияние на его вес. В связи с этим последующие варианты топологии рамы должны быть связаны с ослаблением этого влияния.

В варианте рамы на рис. 2, б за варьирующий параметр принят угол α (15 ≤ α ≤ 55°) между стойкой и наклонным стержнем. В табл. 2 представлены минимальные значения энергии U и веса рамы, а также углы α, при которых они получены. Несовпадение в ряде случаев точек экстремумов объясняется ограничениями в выборе прокатных профилей, о чем говорилось выше.

Наличие двух углов для конкретного пролета требует особого анализа. Например, при l = 9 м оптимальную топологию, исходя из веса, обеспечивает угол 30° (вес при 35° больше на 8,4 %). В то же время потенциальная энергия деформации при угле 30° оказалась больше на 7,8 %, чем при угле 35°. Запас несущей способности оказался большим при угле 35°, что может быть некоторым компенсирующим фактором для этого варианта.

Таблица 2

Характеристики рамы (рис. 2, б)

В варианте рамы на рис. 2, в за варьируемые параметры приняты тот же угол α (15 ≤ α ≤ 60°) и угол наклона ригеля β (5 ≤ β ≤ 30°). Диаграммы, показывающие зависимость энергии U и веса от этих параметров, строятся в пространственных осях координат (рис. 3).

В табл. 3 представлены минимальные значения энергии U и веса рамы. В скобках указаны соответствующие им углы α и β.

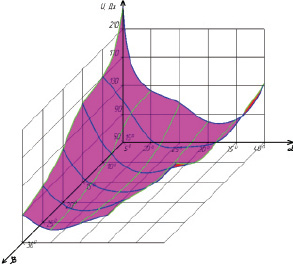
Рис. 3. Диаграма потенциальной энергии деформации для рамы пролетом 9 м

Таблица 3

Характеристики рамы (рис. 2, в)

Комбинации для углов α и β, соответствующие минимальной энергии U и минимальному весу, не совпадают по причинам, указанным выше. Очевидно, и здесь уместен анализ характеристик, подобный проведенному для табл. 2.

Сопоставляя табл. 2 и 3, можно обнаружить уменьшение потенциальной энергии деформации U для пролета 9 (12; 15; 18) м на 40 (50; 79; 70) % и снижение веса для пролета 12 (15, 18) м на 6 (12; 26) %. Преимущество варианта рамы на рис. 2, в по сравнению с рамой на рис. 2, б сказывается при пролете 12 м и особенно при пролетах 15 и 18 м. При пролете 9 м приемлемым оказался вариант на рис. 2, б из-за меньшего веса конструкции.

Рассмотрение рамы на рис. 2, г показало, что введение еще одного наклонного стержня не принесло существенных преимуществ по показателям энергии U и веса по сравнению с вариантом рамы на рис. 2, в. В то же время формирование узла, где сходятся три стержня, усложняет его структуру и увеличивает трудоемкость работ.

Тем самым завершается оптимизация топологии рамы. Приемлемыми оказались варианты: на рис. 2, б при пролете 9 м; на рис. 2, в при пролетах 12, 15 и 18 м. По сравнению с вариантом рамы на рис. 2, а экономический эффект можно определить, сравнивая данные табл. 2 и 3 с данными табл. 1.

Выводы

1. В основу оптимизации топологии положены способы уменьшения изгибающих моментов в балочных элементах рам.

2. Универсальный энергетический критерий оптимальности несущих систем в частном случае конструкции из однородного материала идентичен критерию минимума объема (веса).

3. Использование стандартизированных элементов, в том числе прокатных профилей, влияет на точность решения оптимизационной задачи.

Рецензенты:

Смоляго Г.А., д.т.н., профессор кафедры «Промышленное и гражданское строительство», ГО ВПО «Белгородский государственный технологический университет им. В.Г. Шухова» Министерства образования и науки РФ, г. Белгород;

Лунев Л.А., д.т.н., профессор кафедры «Промышленное и гражданское строительство», Старооскольский технологический институт им. А.А. Угарова (филиал) ФГАОУ ВПО «Национальный исследовательский технологический университет МИСиС Министерства образования и науки РФ, г. Старый Оскол;

Салихов М.Г., д.т.н., профессор, зав. кафедрой автомобильных дорог, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;

Николаев А.П., д.т.н., профессор кафедры «Водохозяйственное строительство», ФГОУ ВПО «Волгоградская государственная сельскохозяйственная академия», г. Волгоград;

Грызлов В.С., д.т.н., профессор кафедры «Строительные технологии и экспертиза недвижимости, ГОУ ВПО «Череповецкий государственный университет», г. Череповец.

Работа поступила в редакцию 05.09.2013.