Скатерть Улама - двумерная плоскость, на которой, начиная с единицы, последовательно по спирали записываются члены натурального ряда (первый этап) и далее из рассмотрения исключаются составные числа (второй этап) (рис. 1). Процедура исключения эквивалентна размещению в ячейках, содержащих составные числа, белых квадратов, в ячейках, содержащих простые числа - черных квадратов. Полученная таким образом фигура в русскоязычной литературе носит название скатерти Улама, в англоязычной литературе - спирали Улама. Один из наиболее известных результатов изучения особенностей распределения простых чисел на скатерти Улама в декартовой системе координат [4, 5] состоит в том, что имеет место некоторая упорядоченность простых чисел - часть из них группируется вдоль диагональных прямых (рис. 2).

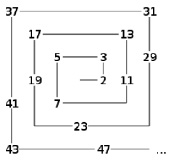
Рис. 1. Создание спирали Улама (слева – первый этап, справа – второй этап)

Рис. 2. Скатерть Улама (общее число членов натурального ряда 105, простых чисел ‒ 9593)[1]
Данный факт позволяет выдвинуть гипотезу о том, что, несмотря на отсутствие в настоящее время аналитических выражений, описывающих связи между простыми числами и позволяющих вычислять их значения, какие-либо устойчивые связи между простыми числами все-таки существуют. Обнаружение данных связей представляет как научный, так и практический интерес.
Материалы и методы исследования
В нашем исследовании мы использовали пакет MATLAB, в котором была создана функция Eratosphen(), реализующая известный алгоритм «Решето Эратосфена» [3]. Входным параметром данной функции является число членов натурального ряда N, среди которых ищутся простые числа. Функция возвращает вектор-строку длиной N, в которой все составные числа натурального ряда заменены нулями.
Листинг файла Eratosphen.m

Ниже представлен результат, возвращаемый функцией Eratosphen().

Затем из вектора, возращенного функцией Eratosfen(), удалялись все нулевые значения, что позволяло получить вектор, содержащий значения простых чисел, упорядоченных в порядке их возрастания.

Далее в полярной системе координат поточечно визуализировалась зависимость значения простого числа от его порядкового номера.
Результаты исследования и их обсуждение
Рассмотрим результаты компьютерного моделирования распределения простых чисел на скатерти Улама в полярной системе координат, представленные на рис. 3. Из рис. 3 видно, что форма распределения простых чисел на скатерти Улама в полярной системе координат при изменении масштаба графика остается неизменной. Таким образом, в полярной системе координат распределение простых чисел оказывается детерминированным фракталом. Значение его фрактальной размерности, полученное в соответствие с алгоритмом Минковского [1], программная реализация которого в пакете MATLAB приведена в [2], оказалось близким 1,75.
а б
б в
в
Рис. 3. Распределение простых чисел на скатерти Улама в полярной системе координат:а – N = 103; б – N = 104; с – N = 105
Также необходимо отметить, что распределение простых чисел на скатерти Улама состоит из 44 спиралей, подобных спиралями Архимеда. Начальная точка каждой спирали совпадает с соответствующим порядковым номером простого числа (i = 1,2,… 44). Простые числа располагаются вдоль спиралей упорядочено - i-й спирали принадлежат числа с номерами i + 44k, k = 0,1,… Примеры зависимостей значений простых чисел, принадлежащих соответствующей спирали, от их порядкового номера представлены на рис. 4 (здесь была использована последовательность, состоящая из N = 107, в которой находится 664581 простых чисела). Из рис. 4 видно, что для простых чисел, принадлежащих i-й спирали, зависимость между значением простого числа и его порядковым номером можно описать, используя для этого аппроксимирующий полином относительно невысокой степени (рис. 5). Данные полиномы, построенные для K простых чисел, можно также использовать для оценки области поиска простых чисел.
а 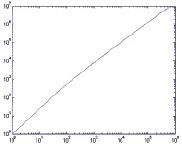 б
б 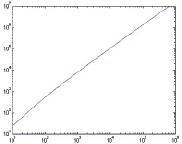
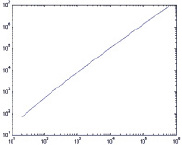 г
г 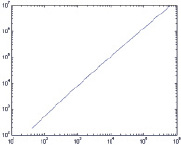
Рис. 4. Зависимость простого числа, принадлежащего i-й спирали от его порядкового номера(по обеим координатным осям использованы логарифмические шкалы):а – i = 1; б – i = 10; в – i = 20; г – i = 44
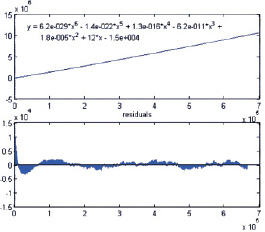
Рис. 5. Зависимость простого числа, принадлежащего спирали i = 1, от его номера и результаты аппроксимации данной зависимости полиномом 6-й степени (внизу ‒ остатки модели)
Заключение
Рассмотрение распределения простых чисел на скатерти Улама в полярной системе координат позволило обнаружить ранее неизвестные закономерности данного распределения, в том числе его структуры и детерминированную связь между простыми числами, принадлежащими соответствующим спиралям изученного распределения.
Приложение. Алгоритм визуализации скатерти Улама и его программная реализация
Для построения алгоритма визуализации скатерти Улама рассмотрим рис. 1. Обозначим единичные шаги вправо, вверх, влево и вниз буквами П, В, Л, Н соответственно. В выбранных обозначениях перемещение из точки 1 в точку 7 (первый виток спирали) будет описываться следующий правилом:
ПВЛЛНН, (1)
из точки 7 в точку 21 (второй виток спирали):
ПППВВВЛЛЛЛНННН, (2)
из точки 21 в точку 43 (третий виток спирали):
ПППППВВВВВЛЛЛЛЛЛНННННН. (3)
Из приведенных выше правил видно, что число шагов в каждом из направлений на k + 1-м витке спирали зависит от числа шагов на k-м шаге спирали:
Шk + 1 = Шk + 2, (4)
где Ш = П, В, Л, Н.
Из приведенного выше описания алгоритма видно, что (1) в терминологии L-систем (Лиденмайер, 1968) [4] - есть аксиома, а (4) - порождающее правило. Соответственно, для визуализации скатерти Улама следует использовать технологию терл-графики [4] (от turtle - черепашка), в которой основным исполнителем является черепашка (точка), которая перемещается по экрану дискретными шагами, прочерчивая или не прочерчивая (как в нашем случае) свой след. «Мгновенное» положение черепашки задается тремя параметрами (x, y, a), где (x, y) - координаты черепашки, a - направление следующего шага. Последовательность команд, определяющих направление перемещения и действия черепашки, задается кодовым словом, буквы которого читаются справа налево. (Примеры программных реализаций алгоритмов терл-графики, используемых для визуализации изображений детерменированных фракталов, можно найти в [5].) Отметим, что здесь наиболее затратной с вычислительной точки зрения оказывается процедура вычисления порождающего правила, представляющего собой рекурсивную процедуру. При построении скатерти Улама вследствие относительной простоты алгоритма перемещения оказывается возможным обойтись без использования рекурсивной процедуры.
Листинг файла Ulam.m



Рецензенты:
Доросинский Л.Г., д.т.н., профессор, зав. кафедрой информационных технологий, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург;
Суханов В.И., д.т.н., доцент, зав. кафедрой микропроцессорной техники, ГАОУ ВПО «Уральский федеральный университет им. первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Работа поступила в редакцию 15.07.2013.
[1] Алгоритм визуализации скатерти Улама и его программной реализации, созданной в пакете MATLAB, представлен в приложении.



