Полупроводниковые материалы широко используются в микроэлектронике и солнечной энергетике. При облучении или термообработках в полупроводниках, как правило, образуется большое количество дислокационных петель, размеры которых весьма различны. При достижении определенного значения радиуса дислокационной петли, который носит название «критический» (rcrit), происходят резкие изменения в плотности дислокационных петель с радиусами больше, чем rcrit. Резкий переход в плотности петель при увеличении их радиуса r > rcrit авторы [6] связывают с переходом частичных дислокаций в полные. Критический радиус дислокационной петли можно рассматривать как важную характеристику, которая показывает те точки, после которых происходят качественные и количественные изменения дефектной сети материала. Поскольку энергия образования дислокационных петель связана с энергией дефекта упаковки материала (ЭДУ), то параметр ЭДУ является важным при анализе процессов дефектообразования и «дефектостойкости». Известно, что с уменьшением ЭДУ происходит увеличение структурных нарушений в металлах [3, 5]. Увеличение концентрации легирующей примеси в кремнии сопровождается снижением энергии дефекта упаковки, что связано с повышением интенсивности формирования примесных выделений [7]. При исследовании полупроводников A2B6 установлено, что интенсивность образования структурных дефектов при облучении электронами уменьшается в последовательности от ZnS → ZnSe ≈ CdS → CdTe ≈ HgTe → ZnTe и далее к GaAs ≈ Si, что коррелирует с ростом значения ЭДУ этих материалов [4].
В данной работе методом просвечивающей электронной микроскопии исследовали монокристаллы полупроводников CdTe, ZnTe, ZnSe, ZnS, CdS, GaAs, Si и Ge, содержащие дислокационные петли, образовавшиеся в результате различных термообработок и (или) облучении электронами и ионами при условиях, подробно описанных в [4]. Монокристаллы полупроводников A2B6 были выращены из газовой фазы в запаянной трубке, а GaAs, Si и Ge были выращены методом Чохральского. Электронно-микроскопические исследования проводили на приборах JEM-100 CX, JEM-4000 EXII и JEM-2100. Образцы для исследования в ПЭМ приготавливали стандартным методом, сначала механически утончая, используя устройство Gatan Dimple Grinder, а затем ионным травлением на установке Precision Ion Polishing System (PIPS), Gatan. Радиус rcrit определяли по методу, предложенному в [6], из гистограмм распределения дислокационных петель по размерам.
На рис. 1 показаны характерные дислокационные петли, образовавшиеся в CdTe в результате ионного травления тонкой фольги ионами Ar+ с энергией 5 keV в течение 15 min.
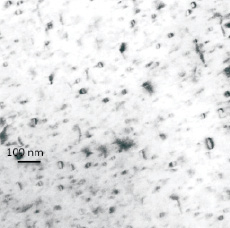
Рис. 1. Образование дислокационных петель в CdTe в результате ионного травления тонкой фольги ионами Ar + с энергией 5 keV в течение 15 min. TEM 220BF изображение
Размеры петель лежат в интервале от 15 до 65 nm при плотности 2,5∙1010 cm–2. Распределение дислокационных петель по размерам показано на рис. 2. Критический радиус в данном случае можно оценить в соответствии с [6] как 48 ± 3 nm. В этой области на рисунке наблюдается резкий скачок в плотности петель (показано стрелкой).
Известно, что процесс образования полной дислокационной петли с вектором Бюргерса 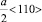 в ГЦК кристаллах можно представить как результат взаимодействия частичных дислокаций Шокли и Франка с векторами Бюргерса
в ГЦК кристаллах можно представить как результат взаимодействия частичных дислокаций Шокли и Франка с векторами Бюргерса 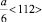 и
и 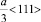 .
.
Например,
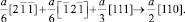 (1)
(1)
Согласно классической модели описания энергий процесса образования дислокационных петель, общая энергия образования дислокационной петли (El, perfect) включает в себя энергию дефекта упаковки дислокационной петли (ESF) и упругую энергию дислокационной линии (El, Frank) [1].
El, perfect = ESF + El, Frank, (2)
где 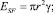 (3)
(3)
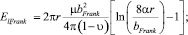 (4)
(4)
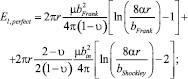 (5)
(5)
r – радиус дислокационной петли; µ – модуль сдвига; υ – коэффициент Пуассона; α – фактор ядра дислокации; bFrank – модуль вектора Бюргерса дислокационной петли Франка; bShockley – модуль вектора Бюргерса дислокационной петли Шокли. В стандартном случае получается 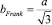 и
и 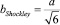 . Здесь a – параметр решетки.
. Здесь a – параметр решетки.
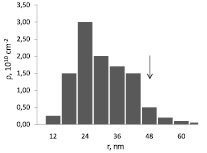
Рис. 2. Зависимость плотности (ρ) дислокационных петель от размеров (r)
Таким образом, из (2)–(5) получаем связь между критическим радиусом rcrit и энергией дефекта упаковки γ как:
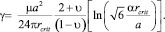 (6)
(6)
В работе [6] проведена оценка ЭДУ в GaInNAs с помощью классической модели образования дислокационных петель и показано, что она не в полной мере описывает экспериментальные результаты. Более энергетически выгодным является процесс образования петель, учитывающий скольжение двух частичных дислокаций Шокли в разных плоскостях. В этом случае формула (2) приобретает вид [6]:
El, perfect = ESF + El, Frank + 2EShockley, (7)
где
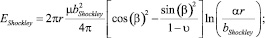 (8)
(8)
здесь β – угол между вектором Бюргерса и дислокационной линией сегмента Шокли, равный π/6.
С учетом уравнений (7) и (8) выражение для γ можно записать как
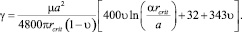 (9)
(9)
Зная значения ЭДУ для полупроводниковых материалов, из уравнения (9) можно рассчитать критические радиусы дислокационных петель для различных полупроводников.
Для решения полученного трансцендентного уравнения использовали программный пакет «Maple».
Значения rcrit для ряда полупроводников представлены в таблице.
Приведенные в таблице значенияrcrit сравнивались с экспериментальными данными, полученными в результате электронно-микроскопических исследований полупроводниковых материалов. Установлено, что рассчитанные по классической модели rcrit не соответствуют экспериментальным значениям и завышены на порядок величины. Значения rcrit, рассчитанные по формуле (9) находятся в хорошем соответствии с экспериментальными значениями (последний столбец таблицы).
Из таблицы также видно, что критический радиус дислокационных петель в полупроводниках напрямую связан с энергией дефекта упаковки материала и уменьшается с ростом ЭДУ. То есть чем выше ЭДУ в материале, тем меньше значение «критического» радиуса и тем более низкая вероятность обнаружить крупные дислокационные петли. Это хорошо согласуется с электронно-микроскопическими исследованиями [4]. В частности, из экспериментов с использованием просвечивающего электронного микроскопа следует, что сульфид цинка, имеющий самую низкую ЭДУ среди исследованных полупроводников, имеет самую высокую плотность и разнообразие структурных дефектов, а размеры дислокационных петель могут достигать значений, на несколько порядков превышающих аналогичные размеры в других анализируемых материалах.
Значения rcrit для ряда полупроводников
|
Материал |
Параметр решетки, nm |
Коэффициент Пуассона [2, 9, 10] |
Модуль сдвига, GPa [2, 9, 10] |
ЭДУ, mJ/m2 [1,4,7,8] |
rcrit, nm |
|
|
Класс. модель |
Класс. модель с уч. дисл. Шокли |
|||||
|
Ge |
0,566 |
0,26 |
31,7 |
90 |
~25,1 |
~ 3,8 |
|
Si |
0,543 |
0,27 |
42,9 |
50-60 |
46,5–58,1 |
7,9–10,1 |
|
GaAs |
0,565 |
0,31 |
32,9 |
55 ± 5 |
40,1–50,2 |
7,8–9,9 |
|
ZnTe |
0,609 |
0,36 |
17,3 |
16 ± 4 |
92,9–171 |
22,5–42,5 |
|
CdTe |
0,648 |
0,41 |
9,2 |
11 ± 1,9 |
95,5–145 |
26,3–41 |
|
ZnSe |
0,566 |
0,28 |
27,5 |
11,4 ± 1,3 |
197–257 |
38,4–51 |
|
CdS |
0,527 |
0,4 |
16,1 |
7,8 ± 1,9 |
162–290 |
44,9–80,2 |
|
ZnS |
0,541 |
0,38 |
21,7 |
5–6 |
405–500 |
110–136 |
|
0,28 |
26,3 |
82–101 |
||||
Таким образом, показано, что имеется корреляция между критическим радиусом ДП и значением ЭДУ. Критический радиус ДП уменьшается с ростом ЭДУ. Поскольку ЭДУ ‒ универсальная величина, указывающая на стойкость материала к дефектообразованию [3–5, 7], то значение «критического» радиуса дислокационной петли можно рассматривать как меру дефектостойкости полупроводников. Чем больше критический радиус ДП, тем менее стоек полупроводник к дефектообразованию и в нем происходит больше структурных нарушений при идентичных режимах воздействия (обработки). При этом размеры и плотность структурных дефектов в материалах при аналогичных условиях обработки зависят от величины энергии дефекта упаковки.
Рецензенты:
Попов А.М., д.ф.-м.н., профессор, Сибирский государственный аэрокосмический университет им. ак. М.Ф. Решетнева, г. Красноярск;
Мисюль С.В., д.ф.-м.н., профессор, Сибирский федеральный университет, г. Красноярск.
Работа поступила в редакцию 11.07.2013.



