Абстрактное понятие полукольца появилось в 30-е годы XX века и в последние десятилетия теория полуколец в связи с широким её применением активно развивается. В самом общем понимании под полукольцом S подразумевают две полугруппы (аддитивную и мультипликативную), связанные законом дистрибутивности умножения относительно сложения с обеих сторон. Именно такое определение полукольца (или ассоциативной алгебры) было дано Вандивером [5] в 1934 году. В той же работе [5] Вандивер упомянул о возможности рассмотрения полуколец с некоммутативным сложением. Мы будем рассматривать полукольца только с некоммутативным сложением. Под циклическим полукольцом будем понимать полукольцо с циклической мультипликативной полугруппой.
Циклическое полукольцо является неизученной алгебраической структурой. Наиболее известными циклическими объектами, близкими к циклическим полукольцам, являются циклические или моногенные полугруппы, циклические группы, циклические кольца [4] (аддитивная группа кольца является циклической), циклические почтикольца [3] (аддитивная группа почтикольца является циклической).
Пусть S = (a) – циклическое полукольцо типа (k, n) с некоммутативным сложением и циклом C. В силу предложений 1 и 2 [6] будем изучать циклические полукольца с единицей, но без нуля.
Строение бесконечных циклических полуколец с коммутативным сложением известно [2]. Конечные циклические полукольца с коммутативным сложением изучает Бестужев А.C. [1].
Теорема 1. Бесконечные циклические полукольца с некоммутативным сложением имеют левое или правое сложение.
Конечные полутела изучены Вейнертом [7]. Вейнерт установил, что конечное полутело изоморфно прямому произведению двух подполутел, одно из которых с левым сложением, а другое с правым сложением. Используя теорему Вейнерта, получено правило сложения в конечных циклических полуполях:
Предложение 1. Пусть C = (c) – циклическое полуполе порядка n, |C + 1| = m, |1 + C| = h. Тогда сложение в C выполняется по формуле (для любых i1, j1, i2, j2∈ N0):
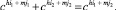
Теорема 2. Цикл C конечного циклического полукольца S = (a) типа (k, n) с некоммутативным сложением является циклическим полуполем с образующим элементом a(nl + 1) и единицей anl для некоторого l ∈ N0 такого, что nl ≥ k > n(l – 1).
Циклические полукольца с некоммутативным сложением могут иметь идемпотентное и неидемпотентное сложение. Рассмотрим сначала полукольца с идемпотентным сложением.
Теорема 3. Всякое конечное циклическое полукольцо S = (a) типа (k, n) с идемпотентным некоммутативным сложением и с поглощающим элементом ak имеет либо левое сложение, либо правое сложение.
Бинарное отношение ~, заданное на полукольце S формулой x ~ y ⟺x, y ∈ C или x = y, является конгруэнцией. Факторполукольцо S/~ является циклическим полукольцом с поглощающим элементом [ak]~.
Любое конечное циклическое полукольцо с идемпотентным некоммутативным сложением сводится к подобному полукольцу с поглощающим элементом и конечному циклическому полуполю:
Теорема 4. Пусть в конечном циклическом полукольце S = (a) типа (k, n), k ≥ 1, n ≥ 2, сложение не коммутативно, не левое и не правое. Тогда:
1) 1 + anl = anl + 1 = anl, где anl – единица цикла C полукольца S для такого натурального l, что n(l – 1) < k ≤ nl;
2) множество T = {1, an, a2n, …, anl}, является циклическим подполукольцом в полукольце S, имеющим коммутативное сложение и поглощающий элемент anl.
3) для любых r, s ∈ N0, где r – s ≢ 0(mod n), выполняется:
ar + as = a(r + nl) + a(s + nl).
В следующей теореме показываются существование и единственность полукольца со структурой, описанной в теореме 4.
Теорема 5. Пусть даны натуральные числа k, n, l такие, что n ≥ 2 и n(l – 1) < k ≤ nl, произвольное циклическое полукольцо T = {1, b, b2, …, bl} с идемпотентным коммутативным сложением и с поглощающим элементом bl с условием 1 + bl = bl, и некоторое циклическое полуполе C = {1, c, c2, …, c(n – 1)} . Тогда существует единственное с точностью до изоморфизма конечное циклическое полукольцо S = (a) типа (k, n) с идемпотентным некоммутативным сложением, не левым и не правым такое, что его подполукольцо {1, an, a2n, …, aln} изморфно T, а его цикл {ak, a(k + 1), …, a(k + n – 1)} изоморфен C.
Пусть теперь S = (a) – циклическое полукольцо типа (k, n) с неидемпотентным некоммутативным сложением и циклом C. Обозначим m = |C + e|, h = |e + C|.
Конечное циклическое полукольцо с неидемпотентным некоммутативным сложением сводится к подобному полукольцу с поглощающим элементом и конечному циклическому полуполю при некоторых условиях.
Пусть произвольные натуральные числа r и s имеют разложения r = hi1 + mj1, s = hi2 + mj2, для некоторых целых чисел i1, j1, i2, j2.
Теорема 6. Пусть даны произвольные натуральные числа k и n, произвольное циклическое полукольцо S′ = {1, a, a2, …, ak} с неидемпотентным некоммутативным сложением и поглощающим элементом ak, некоторое циклическое полуполе C’ = {e = cn, c, c2, …, c(n – 1)} порядка n, где |C’ + e| = m, |e + C’| = h. Циклическое полукольцо S = (a) типа (k, n), факторполукольцо которого по конгруэнции ~ совпадает с полукольцом S′, то есть S/~ = S′, а цикл C полукольца S изоморфен полуполю C′, то есть ⟨C, + ,∙⟩ ≅ ⟨C′, + ,⟩, существует тогда и только тогда, когда в S′ для любых r, s ∈ N0 выполняется условие:
ar + as = at,
где t ≡ hi1 + mj2(mod n); t > max{r, s}.
Предложение 2. Хвост T полукольца S из теоремы 6 совпадает с S′\{ak}, то есть ⟨T, + ,∙⟩ = ⟨S′\{ak}, + ,∙⟩, только в случае |C′| = 1.
Рассмотрим циклическое полукольцо S = (a) типа (k, n) с неидемпотентным некоммутативным сложением и коротким хвостом (k ≤ n).
Пусть натуральное число z такое, что 0 ≤ z ≤ k + n – 1 имеет разложения:
z = hi1 + mj1, (1)
где 1 ≤ mj1 ≤ n;
z = hi2 + mj2, (2)
где 1 ≤ hi2 ≤ n.
Теорема 7. Если полукольцо S = (a) типа (k, n), где k ≤ n, имеет некоммутативное сложение, цикл C изоморфен прямому произведению подполутел C + e и e + C порядков m и h соответственно, то выполняются равенства:
(a) 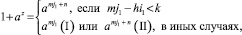
где z удовлетворяет (1).
(б) 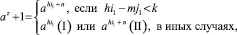
где z удовлетворяет (2).
Количество полуколец типа (k, n) с неидемпотентным некоммутативным сложением при k ≤ n
|
(k, n) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
0 |
2 |
2 |
2 |
2 |
4 |
2 |
2 |
2 |
4 |
2 |
4 |
|
2 |
2 |
2 |
2 |
2 |
4 |
2 |
2 |
2 |
4 |
2 |
4 |
|
|
3 |
2 |
2 |
2 |
4 |
2 |
2 |
2 |
4 |
2 |
4 |
||
|
4 |
2 |
2 |
6 |
2 |
2 |
2 |
4 |
2 |
4 |
|||
|
5 |
2 |
10 |
2 |
2 |
2 |
4 |
2 |
6 |
||||
|
6 |
6 |
2 |
2 |
2 |
10 |
2 |
6 |
|||||
|
7 |
2 |
2 |
2 |
18 |
2 |
10 |
||||||
|
8 |
2 |
2 |
10 |
2 |
6 |
|||||||
|
9 |
2 |
18 |
2 |
18 |
||||||||
|
10 |
10 |
2 |
50 |
|||||||||
|
11 |
2 |
34 |
||||||||||
|
12 |
18 |
С помощью программы, написанной на языке Си, в которой учтены необходимые условия, сформулированные в теореме 7, по заданным числам m, h и k можно находить полукольца S = (a) типа (k, n) с неидемпотентным некоммутативным сложением, где n = m∙h, |C + e| = m, |e + C| = h. В таблице приведено количество полуколец типа (k, n) с неидемпотентным некоммутативным сложением для n ≤ 12.
Найденные полукольца показывают, что теорема 7 дает лишь необходимые условия существования циклических полуколец с неидемпотентным некоммутативным сложением и коротким хвостом.
Следующая теорема дает достаточное условие на сложение в мультипликативной циклической полугруппе, превращающее ее в циклическое полукольцо с неидемпотентным некоммутативным сложением:
Теорема 8. Пусть дана циклическая полугруппа S = (a) типа (k, n), n ≥ 2. Тогда для любых натуральных чисел m, h и l, таких, что m∙h = n, (m, h) = 1 и nl ≥ k > n(l – 1), на S существует неидемпотентное некоммутативное сложение, определяемое равенствами:
(a) 
где z удовлетворяет (1),
(б) 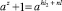
где z удовлетворяет (2), превращающее S в циклическое полукольцо.
Теорема 9. В циклическом полукольце S = (a) типа (k, n), где k ≤ n, с неидемпотентным некоммутативным сложением сумма любых трех элементов лежит в цикле C.
Теорема 10. Пусть S = (a) – циклическая полугруппа типа (k, n), где k ≤ n, со сложением, заданным правилами (a) и (б) из теоремы 7 и удовлетворяющим закону дистрибутивности. Тогда для того, чтобы S было полукольцом, необходимо и достаточно выполнение следующих условий (для любых r, s ∈ N0):
(a) 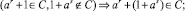
(б) 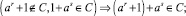
(в) 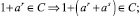
(г) 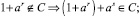
(д) 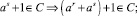
(е) 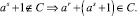
Для полного описания циклических полуколец с некоммутативным сложением осталось описать такие полукольца с неидемпотентным сложением и поглощающим элементом.
Автор выражает благодарность своему научному руководителю профессору Е.М. Вечтомову за постановку задачи и постоянное внимание к работе.
Рецензенты:
Вечтомов Е.М., д.ф.-м.н., профессор, зав. кафедрой алгебры и дискретной математики, Вятский государственный гуманитарный университет, г. Киров;
Чермных В.В., д.ф.-м.н., профессор, доцент кафедры алгебры и дискретной математики, Вятский государственный гуманитарный университет, г. Киров.
Работа поступила в редакцию 15.01.2013.



