Почти каждый день в жизни любого человека возникает проблема выбора. Например, пойти или не пойти куда-либо, сделать или не сделать что-либо, сказать или промолчать и т.д. Вопросы такого характера, несомненно, присутствуют в нашей жизни. При этом каждый отвечает на них по-своему, руководствуясь различными фактами, имеющимися знаниями и опытом, и, что немаловажно, мнением других людей, которым доверяют или к которым привязаны. Примером влияния одного человека на принятие решения другим человеком может служить классическая ситуация взаимодействия любого родителя со своим ребенком, когда ребенок попросту не в состоянии принять решение и, как следствие, всецело опирается на мнение родителей.
Проблема осуществления выбора может быть неразрывно связана с проблемой ступора. Ситуация ступора может возникнуть тогда, когда ни одна из альтернатив еще не принята в качестве окончательного выбора. При этом у человека может появиться скованность или замедление мыслей, чувств и движений, что можно считать негативными последствиями.
Безусловно, в некотором будущем в процессе развития современных технологий и науки неотъемлемой частью человеческого общества станут и человекоподобные роботы. При этом почти со стопроцентной долей уверенности можно говорить, что и у человекоподобных роботов по мере их совершенствования и усложнения их функционала возникнет проблема выбора в условиях социальной привязанности, характерная в настоящее время для всех людей.
Согласно современным определениям, привязанность – это чувство близости, основанное на глубокой симпатии, преданности кому или чему-либо; поиск и установление эмоциональной близости с другим человеком [2, 7].
Основоположником теории привязанности является известный английский психиатр и психоаналитик, специалист в области психологии развития, психологии семьи, психоанализа и психотерапии Джон Боулби [1]. В своей книге «Эмоциональная машина» [8] Марвин Минский анализирует работы Боулби и ряда других психологов и строит ряд абстрактных моделей того, как работает человеческий мозг, включая то, как привязанность может влиять на цели и действия людей. Несомненным преимуществом анализа, проведенного Минским, является максимальная общность предлагаемых моделей. В то же время Минский не дает каких-либо конкретных рекомендаций по применению данных моделей.
Современная робототехника стоит на пути моделирования привязанности роботов к их владельцам и определения поведения роботов в зависимости от этой привязанности. В этом направлении можно выделить следующие известные проекты: японский робот-пес Aibo, робот-тюлененок PARO, робот-динозаврик PLEO [3-6].
В настоящей статье предлагаются математическая модель привязанности робота, алгоритм принятия решения роботом в условиях привязанности, а также рассмотрена ситуация ступора в рамках предложенной модели. Модель и алгоритм строятся на основе следующих псевдоэмоциональных характеристик робота.
Псевдоэмоциональные характеристики робота и привязанность
Из теории психологии человека известно, что эмоции являются ответной реакцией организма на некий раздражитель-стимул. Для роботов этот стимул будем называть сюжетом и пусть он имеет следующее определение.
Пусть t – время.
Функцию S(t) будем называть сюжетом, если она обладает следующими свойствами:
1. Область определения S(t): t ∈ [t0, T0], 0 < t0 < T0 < ∞.
2. 0 < S(t) < ∞ для любого t ∈ [t0, T0].
3. S(t) – непрерывная и взаимнооднозначная функция на [t0, T0].
Функцию f(t), удовлетворяющую соотношению f(t) = a(S(t), t)S(t), где a(S(t), t) – произвольная функция, назовем функцией внутренних переживаний робота (область определения f(t), a(S(t), t) и S(t) совпадают).
Функцию внутренних переживаний робота M(t) назовем псевдоэмоцией робота, если она удовлетворяет условиям:
1. Область определения M(t): t ∈ [t0, T0], 0 < t0 < T0 < ∞.
2. M(t) – дифференцируемая на (t0, T0), непрерывная и однозначная функция на [t0, T0].
3. M(t0) = 0 и M(T0) = 0.
4. В области определения существует единственная точка z, такая, что: z ≠ t0, z ≠ T0 и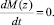 
Под псевдовоспитанием робота или просто псевдовоспитанием будем понимать относительно устойчивое отношение робота к сюжету.
Элементарным псевдовоспитанием робота r(t) на сюжете S(t) назовем функцию вида:
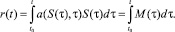
Будем считать, что с течением времени робот забывает псевдоэмоции, которые он когда-то испытывал. Прошлые псевдоэмоции все меньше и меньше сказываются на его текущем псевдовоспитании. А вместе с тем забываются и прошлое элементарное псевдовоспитание, порождаемое испытываемыми ранее псевдоэмоциями робота.
Исходя из этого введем следующее определение:
Псевдовоспитанием робота R(t) (псевдовоспитание робота во время действия псевдоэмоции) на сюжете S(t) назовем функцию вида:
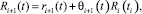
где t – текущее время, t > ti, 0 ≤ θi+1(t) ≤ 1. Текущее время удовлетворяет соотношению t = τ + ti, где τ – время действия текущей псевдоэмоции от начала ее проявления, ti – время функционирования (псевдовоспитания) робота до появления текущей псевдоэмоции, Ri(ti) – псевдовоспитание, полученное роботом ко времени ti. Нижний индекс i означает, что до момента действия текущей псевдоэмоции робот уже испытал i псевдоэмоций. Кроме этого, будем подразумевать, что процесс псевдовоспитания является непрерывным в том смысле, что на смену одной псевдоэмоции приходит сразу же другая псевдоэмоция, порожденная очередным сюжетом с порядковым номером i + 1.
Коэффициент θi(t) будем называть коэффициентом памяти прошлых событий или коэффициентом памяти.
Под псевдовоспитательным процессом будем понимать процесс изменения значения функции псевдовоспитания робота. В начальный момент времени значение функции псевдовоспитания робота равно нулю.
Таким образом, будем считать, что величина функции псевдовоспитания Ri(t) будет показывать привязанность робота к некоторому субъекту, который ассоциируется с воздействием на робота последовательностью сюжетов S1(t)...Si(t). Если на робота оказывается воздействие со стороны n различных субъектов, каждый из которых характеризуется последовательностью раздражителей: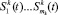 
, где k – порядковый номер субъекта, mk – количество сюжетов воздействия со стороны k-го субъекта, то величины функций псевдовоспитания 
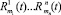показывают привязанность робота относительно каждого из воздействующих субъектов. В дальнейшем будем предполагать, что коэффициенты памяти робота могут быть различным в зависимости от каждого конкретного воздействующего сюжета.
Рассмотрим упрощение предложенной модели, для этого введем несколько определений.
Забывчивым роботом будем называть робота, для псевдовоспитательного процесса которого характерно:
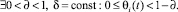
При этом, если в момент окончания любой псевдоэмоции коэффициент памяти прошлых событий θi(t) = θ, то робота будем называть равномерно забывчивым роботом.
Псевдоэмоции M1(t), ..., Mn(t), влекущие одинаковое элементарное псевдовоспитание q, то есть r1(T0) = ... = rn(T0) = q, будем называть равноценными псевдоэмоциями. При этом будем говорить, что осуществляется процесс псевдовоспитания на равноценных псевдоэмоциях с элементарным псевдовоспитанием q.
Таким образом, учитывая вышесказанное, можно получить следующий результат.
Для равномерно забывчивого робота с коэффициентом памяти прошлых событий θ, псевдовоспитательный процесс которого осуществляется на равноценных псевдоэмоциях с элементарным псевдовоспитанием q, значение функции псевдовоспитания в момент окончания ощущения i-й псевдоэмоции вычисляется как
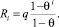
Принятие решения роботом в условиях социальной привязанности
Предположим, что перед роботом возникает проблема выбора, которая заключается в следующем: робот должен принять некоторое решение относительно своих дальнейших действий или поведения. При этом робот должен учитывать свои социальные связи и социальную привязанность к владельцу при принятии решения. Например, когда два человека дают роботу одновременно две взаимоисключающие команды, робот должен принять решение в пользу той или иной командыв зависимости от своей привязанности к каждому из людей-владельцев робота.
Пусть на робота действует n различных субъектов с последовательностями раздражителями-сюжетами: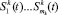 
. Таким образом, к некоторому моменту времени функционирования робота у него сложились псевдовоспитания 
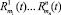относительно каждого из раздражителей, то есть относительно каждого из воздействующих субъектов.
Принимая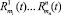 
в качестве меры привязанности робота относительно каждого из воздействующих субъектов, можем сформулировать простое правило принятия роботом решения в пользу того или иного субъекта: решение принимается в пользу того субъекта, относительно которого сформировалось максимальное псевдовоспитание. При этом возникает вопрос что делать роботу, если максимальное псевдовоспитание сформировалось сразу относительно нескольких субъектов? В какой последовательности реагировать на воздействия или быть может оставить некоторые воздействия попросту без реакции? Данную ситуацию будем называть ситуацией ступора.
Принятие решения роботом и ситуация ступора
Предположим, что из n действующих на робота субъектов, относительно p субъектов у робота в момент принятия решения сформировалось максимальное псевдовоспитание, то есть
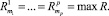
Пусть робот является равномерно забывчивым относительно каждого из воздействующих субъектов с коэффициентом памяти прошлых событий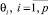 
,и псевдовоспитательный процесс относительно каждого из воздействующих субъектов происходит на равноценных псевдоэмоциях с элементарными псевдовоспитаниеми q. Тогда ситуация ступора будет выглядеть следующим образом:
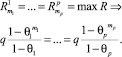
Сократив предложенное соотношение на q, получаем условие ступора для равномерно забывчивого робота с псевдовоспитательным процессом на равноценных псевдоэмоциях:
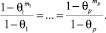
Как видно из условия ступора, независимо от коэффициентов памяти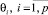 
при m1 = ... = mp = 1 условие ступора выполняется всегда. Данный случай является тривиальным, поэтому далее при рассмотрении условия ступора будем предполагать, что m1, ..., mp не равны единице одновременно.
Разумно предположить, что лучше, чем искать решения для преодоления ситуации ступора, необходимо искать возможность для того чтобы вовсе не попадать в данную ситуацию. Очевидно, что робот никогда не придет в ступор, если для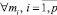 
и заданных 
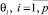полученное условие ступора никогда не будет выполняться. Коэффициенты памяти прошлых событий, для которых при любых натуральных значениях 
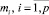, условие ступора не выполняется, назовем антиступорными коэффициентами памяти.
Покажем, что антиступорные коэффициенты памяти существуют. Рассмотрим ситуацию, когда ступор возникает относительно двух субъектов. Условие ступора в данном случае выглядит следующим образом:
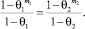
Пусть выполняется: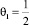 
и 
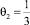. Таким образом, получим соотношение:
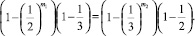
Преобразовав, получаем: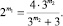 
Из полученного соотношения можно сделать вывод, что, при m1 и m2, одновременно не равных единице, условие ступора никогда не выполняется. Докажем это.
Рассмотрим левую часть равенства. Возможные значения, которые будет принимать левая часть, при бесконечном увеличении m1 – это: 2, 4, 8, 16, ... В то же время правая часть равенства при бесконечном увеличении m2, будет стремиться от 2 к 4, при этом никогда не достигнув 4. Таким образом, при m1 и m2 одновременно не равных единице, условие ступора никогда не выполнится.
Аналогичным образом можно показать, что для трех субъектов коэффициенты памят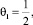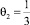и 
и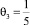 
являются также антиступорными.
Таким образом, зная коэффициенты памяти равномерно забывчивого робота, можно делать прогноз по поводу того, как возможно робот будет себя вести при принятии решений. Попадет ли он в ступор или такая ситуация в принципе невозможна.
Заключение
В статье представлена модель принятия решения роботом в условиях социальной привязанности, основанная на введенных псевдоэмоциональных характеристиках. Модель является достаточно простой, но в то же время не исключающей общности, что является несомненным преимуществом. Для того чтобы применить модель в конкретной предметной ситуации, достаточно определить всего две функции: функцию сюжета и функцию псевдоэмоции, что является одновременно преимуществом и недостатком. Преимущество заключается в том, что этих функций всего две. С другой стороны, определить конкретный вид данных функций вне зависимости от предметной области не представляется возможным.
Кроме этого, рассмотрена ситуация ступора в рамках предложенной модели принятия решения роботом. Сформулировано условие наступления ступора. Показано, что для определенного класса роботов ситуацию ступора можно достаточно просто предугадать или попросту избежать.
Рецензенты:
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и информационной безопасности, ФГБОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь;
Тарунин Е.Л., д.ф.-м.н., профессор кафедры прикладной математики и информатики, ФГБОУ ВПО «Пермский государственный национальный исследовательский университет», г. Пермь.
Работа поступила в редакцию 11.01.2013.