Изобретенные в середине XX в. нейрокомпьютеры и нейронные сети прошли путь от ажиотажного восхищения в 50-х гг. через критику, отрицание и забвение в 60-х – 70-х гг. к всеобщему признанию и массовому применению, наблюдаемым в настоящее время. Вместе с тем, несмотря на пик популярности, обращает на себя внимание отсутствие общепринятых унифицированных технологий нейросетевого моделирования, что, по-видимому, объясняется несовершенством теоретической базы. Профессионалы-разработчики нейросетевых интеллектуальных систем, приступая к решению практически каждой новой задачи, применяют весьма внушительный арсенал различных, только им известных хитростей и ноу-хау, зачастую надеясь на интуицию и даже просто на везение. В России, как и зарубежом, существуют научные школы, которые активно развивают и применяют на практике свои собственные варианты нейросетевых парадигм и технологий, отмечают их преимущества, часто противопоставляя другим подходам, применяемым в других школах.
Пермской научной школой искусственного интеллекта (www.PermAi.ru) на протяжении последних пятнадцати лет предпринимались попытки изобретения новых принципов построения и функционирования нейронных сетей. Осваивались пропагандируемые другими научными школами нейросетевые парадигмы неклассического типа. Однако до сих пор не нашлось практически значимых задач, для решения которых неклассические нейросети оказались бы более эффективны, чем персептроны с сигмоидными активационными функциями. Нами накоплен обширный опыт применения таких нейросетевых математических моделей в промышленности [6, 14, 16, 19, 22−24], экономике и бизнесе [1, 14, 16, 19, 21, 22, 24, 28], политологии и социологии [14, 19, 22, 24, 25, 33], науковедении [1, 19] криминалистике [5, 9, 14, 16, 19, 22, 24, 26, 27, 30, 31], спорте [29], экологии и энергосбережении [2, 3], педагогике [10, 11, 24, 32], в исторической науке [7], медицине [4, 14, 16, 19, 20, 22, 24], туризме [15] и в других предметных областях. Обобщенный алгоритм нейросетевого моделирования, применяемый во всех этих проектах, приведен на рисунке 1, включает следующие этапы.
1. Постановка задачи. На этом этапе определяются цели моделирования, устанавливаются входные и выходные параметры модели, устанавливается структура (состав и длина) входного вектора X и выходного вектора D.
2. Формирование примеров. Формируется содержимое входных и выходных векторов. Cоздается множество пар Xq – Dq (q = 1, ..., Q). Каждая такая пара составляет пример, характеризующий предметную область.
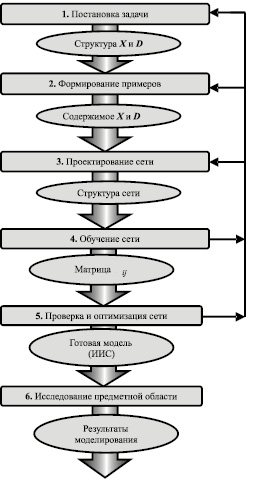
Алгоритм нейросетевого математического моделирования
Все множество примеров разбивают на обучающее L и тестирующее T. В особо ответственных случаях помимо обучающего множества L и тестирующего множества T формируется еще и подтверждающее множество P из примеров, принадлежащих той же самой предметной области, но не пересекающееся ни с множеством L, ни с множеством P.
3. Первоначальное проектирование сети. Структура персептрона выбирается из следующих соображений. Число входных нейронов Nx должно быть равно размерности входного вектора X. Число выходных нейронов Ny должно быть равно размерности выходного вектора D. Число скрытых слоев, согласно теореме Арнольда–Колмогорова – Хехт−Нильсена, должно быть не менее одного. На последующих этапах число скрытых слоев может корректироваться, если это позволит улучшить качество работы сети. Число нейронов в скрытых слоях рассчитывается с помощью формул следствия из теоремы Арнольда–Колмогорова – Хехт−Нильсена [16]. На последующих этапах число нейронов в скрытых слоях может корректироваться, если это позволит улучшить качество работы сети.
4. Обучение сети. Цель обучения – подобрать синаптические веса wij так, чтобы на каждый входной вектор Xq множества обучающих примеров сеть выдавала вектор Yq, минимально отличающийся от заданного выходного вектора Dq. Эта цель достигается путем использования алгоритмов обучения нейронной сети. С целью повышения качества обучения применяются методы обнаружения и исключения противоречивых примеров, посторонних выбросов и малозначимых входных нейронов по методикам, предложенным в [12, 16, 21].
5. Проверка и оптимизация сети. Проверка обобщающих свойств сети производится на тестирующем множестве примеров, т.е. на тех примерах, которые не были использованы при обучении сети.
Если на тестирующем множестве примеров разница между компонентами желаемого выходного вектора Dq и действительного выходного вектора Yq окажется незначительной, то можно переходить к следующему этапу 6, не выполняя оптимизацию сети. Однако, чтобы лишний раз убедиться в адекватности разрабатываемой нейросетевой математической модели, полезно вернуться на этап 2 и те примеры, которые были тестирующими (либо часть тестирующих примеров), включить в обучающее множества, а часть примеров, бывших обучающими, сделать тестирующими. После этого снова повторить этапы 3, 4, 5.
Если же погрешность обобщения сети окажется неприемлемо большой, то надо попытаться оптимизировать сеть. Оптимизация сети состоит в подборе наиболее подходящей для данной задачи структуры сети – количества скрытых слоев, количества скрытых нейронов, количества синаптических связей, вида и параметров активационных функций нейронов. Оптимизация нейронной сети подразумевает многократные возвраты назад – на этапы 4, 3, 2, и даже на этап 1, на котором заново выполняется постановка задачи, включающая переоценку значимости входных параметров с последующим их сокращением или, наоборот, добавлением. После оптимизации сети ее обобщающие свойства проверяются на примерах подтверждающего множества P. Результатом оптимизации и проверки сети является готовая к использованию нейросетевая математическая модель предметной области – интеллектуальная информационная система.
6. Исследование предметной области. Путем проведения вычислительных экспериментов над математической нейросетевой моделью достигаются цели моделирования, находятся ответы на все поставленные вопросы. Например, могут быть решены такие задачи, как оптимизация моделируемого объекта или процесса, прогнозирование его будущих свойств, выявление закономерностей предметной области и др.
Таким образом, в результате выполнения приведенного на рисунке алгоритма метода нейросетевого математического моделирования получаются два вида продуктов:
– После выполнения этапа 5 создается готовая к использованию интеллектуальная информационная система, являющаяся математической моделью предметной области.
– После выполнения этапа 6 получаются результаты исследования предметной области методом нейросетевого математического моделирования. Эти результаты обычно представляются в виде таблиц, графиков, номограмм, гистограмм, иллюстрирующих обнаруженные закономерности предметной области, результаты оптимизации, прогнозирования и др.
Применения метода нейросетевого математического моделирования в указанных выше предметных областях позволило получить новые научные знания, имеющие как научное, так и практическое значение. Так, при решении задачи диагностики авиационных двигателей [14, 16] зафиксировано свойство, названное «интуицией нейронных сетей» – способность делать правильные выводы и заключения на неполной для логического вывода информации. Конкретно это свойство проявилось в том, что нейронная сеть ставила диагнозы таких неисправностей двигателей, которые традиционными методами диагностики, основанными на явных знаниях, не обнаруживаются. В работе [14] опубликован подтвердившийся впоследствии нейросетевой прогноз результатов выборов Президента России за два года до их начала, когда исход выборов очевидным еще не представлялся. В [14] предложены нейросетевые методики прогнозирования банкротств предприятий, оценки банковских рисков, оценки недвижимости и др. с учетом общеэкономического положения в стране и в мире, что повысило устойчивость моделей по отношению к форс-мажорным явлениям: экономическим кризисам, спадам и подъемам. В результате разработки нейросетевой системы диагностики заболеваний сердечно-сосудистой системы [19] выявлены новые, неисследованные ранее медицинские знания и закономерности, которые рекомендуется учитывать практикующим врачам. Применение нейронных сетей для анализа полиграмм в практике детекции лжи [5, 30] позволило повысить точность заключений полиграфного аппарата на 7–10 %, что можно объяснить способностью нейронных сетей извлекать новые неизвестные экспертам закономерности моделируемых предметных областей и использованием этих закономерностей при формировании заключений. При проектировании системы прогнозирования курсов валют [14] зафиксирован эффект увеличения точности прогнозов в случае учета факторов астрологической природы, влияние которых на результаты прогнозирования в рамках классической науки объяснить не представляется возможным. При разработке нейронной сети, предназначенной для определения склонности человека к научной и к предпринимательской деятельности [1] также выявлено влияние астрологических факторов, учет которых повышает точность прогнозирования, что однако не поддается логическому объяснению в рамках известных знаний. В [8] поставлен вопрос о влиянии социального фактора в эволюционной теории Дарвина и предложен способ учета этого фактора в виде социально-генетического алгоритма, эффективного при обучении нейронных сетей. В [13] выполнены теоретические исследования границ возможностей метода нейросетевого моделирования, а в [12] предложена оригинальная методика выявления посторонних выбросов статистической информации с помощью нейронной сети. В работах [18, 23] предложена библейско-философская концепция цели развития цивилизации и искусственного интеллекта.
Рецензенты:
Русаков С.В., д.ф.-м.н., профессор, заведующий кафедрой прикладной математики и информатики, Пермский государственный национальный исследовательский университет, г. Пермь;
Пенский О.Г., д.т.н., доцент, профессор кафедры процессов управления и компьютерной безопасности, Пермский государственный национальный исследовательский университет, г. Пермь.
Работа поступила в редакцию 11.01.2013.



