На сегодняшний день невозможно представить жизнь современного человека без лазерных технологий, которые применяются в различных областях, таких, как медицина, машиностроение, электроника, связь и т.д. Лазерное излучение обладает рядом уникальных характеристик – монохромность, высокая степень временной и пространственной когерентности, малая расходимость луча, большая плотность мощности, а также возможность управлять ими. Использование лазерных технологий в медицине открывает новые возможности, начиная от эстетической медицины до сложного медицинского вмешательства, позволяет реализовать принципиально новые решения и использовать новые материалы, повышающие качество лечения. Лазерные биотехнологии можно разделить в зависимости от плотности мощности лазерного излучения на лазерную диагностику, лазерную терапию, лазерную хирургию или деструкцию биотканей, в основе которой лежит термический фактор. Кроме того, лазерные технологии имеют дело с живой материей, которая представляет собой многослойные сложные структуры, с различными тепловыми и оптическими свойствами, что приводит к необходимости учитывать анизотропию физических параметров тканей и гомеостаз живого объекта [2].
Разработка модели
Важнейшими параметрами, определяющими взаимодействие лазерного излучения с биотканиями, являются: режим облучения (непрерывный или импульсный), время и мощность, а также длина волны, которая определяет интенсивность поглощения излучения тканью.
Распределение температуры является одним из основных параметров в лазерных биотехнологиях. Термические свойства биотканей определяются ее многослойной структурой, теплопроводностью и теплоемкостью. Поглощенная энергия лазерного излучения вызывает в облученном участке локальное повышение температуры. При этом часть тепла отводится из зоны обработки за счет кондукции в окружающие области, вызывая зачастую нежелательный нагрев. Расчет режима обработки позволяет минимизировать нагрев окружающих тканей.
В настоящее время все более широко используются системы инженерного анализа для постановки численных экспериментов и нахождения оптимальных параметров в исследуемой области. Это позволяет значительно сократить время и стоимость разработки и исследования, рассчитать оптимальные технологические параметры. Разработка модели позволит найти оптимальные режимы лазерной обработки биологических тканей вплоть до расчета индивидуального режима для каждого слоя и минимизировать тепловое воздействие на окружающие ткани.
Распределение температуры в анизотропном твердом теле описывается уравнением теплопроводности, которое в операторной форме имеет вид [3]:
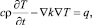(1)
где с – удельная теплопроводность; ρ – плотность; Т – температура в структуре;
t – время; ∇ – оператор Набла; k – коэффициент теплопроводности; q – источник
тепла.
Источником тепла является лазерное излучение, которое частично отражается от обрабатываемей поверхности, поглощается материалом и проникает в него. Затухание лазерного луча за счет поглощения его энергии телом описывается законом Ламберта [3]:
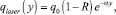(2)
где qleser(y) – плотность мощности лазерного луча с учетом затухания; q0 – плотность мощности лазерного луча; R – коэффициент отражения; α – поглощательная способность среды; y – координата направленная в глубь материала от обрабатываемой поверхности.
Излучательный и конвекционный процессы отвода тепла с обрабатываемой поверхности будут описываться следующими выражениями [3];
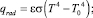(3)
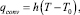(4)
где ε – коэффициент излучения; σ – постоянная Стефана-Больцмана; h – конвективный коэффициент; qrad, qconv – плотность теплового потока за счет излучения и конвекции соответственно; T0 – температура окружающей среды.
Суммарный тепловой поток qconb с поверхности будет описываться выражением:
(5)
где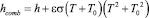 
– суммарный коэффициент теплопередачи.
В модели лазерной обработки биотканей учтены следующие тепловые потоки: поглощенная телом энергия лазерного луча, конвективный отвод тепла и излучение с поверхности. На рис. 1 схематично показаны потоки тепла, которые учитываются в разрабатываемой модели. Был взят двумерный случай, поскольку распределение температуры по z координате будет аналогично x, а уменьшение размерности позволит сократить время расчетов.
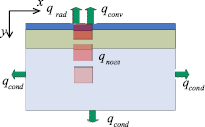
Рис. 1. Тепловые потоки
в разработанной модели
Для двумерного нестационарного случая и анизотропной среды в частных производных уравнение (1) будет иметь следующий вид:
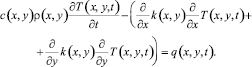(6)
Граничные условия с учетом уравнения Фурье [2] будут следующими:
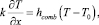(7)
для верхней грани, параллельной оси у;
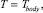(8)
для нижней грани, параллельной оси у, и для граней, параллельных оси x.
Уравнение (6) с учетом граничных условий (7) и (8) не может быть решено аналитически. Поэтому для ее решения был использован численный метод [3].
Исходя из геометрии задачи (см. рис. 1), необходимо создать прямоугольную координатную сетку, равномерную по оси x и неравномерную по оси y. При выборе шага по оси x необходимо учитывать ширину лазерного луча, чтобы минимальный шаг был меньше его ширины. По оси y необходима неравномерная сетка, поскольку обрабатываемые слои в биологических структурах имеют различную толщину от десятков микрон до сантиметров.
Введение координатной сетки предполагает, что значения всех переменных и их производных рассматриваются только в узлах этой сетки. Поэтому все переменные заменятся сеточными функциями, а все производные – конечными разностями.
На рис. 2 представлены сеточная модель и направление осей координат.
Исходная система дифференциальных уравнений в частных производных (6), с учетом граничных условий (7)–(8) и выражения для лазерного излучения (2) на сетке, представленной на рис. 2, преобразованная в систему алгебраических уравнений, имеет вид [1]:
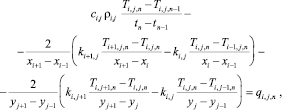(9)
для внутренних точек области i = 2...I – 1, j = 2...J – 1, n = 2...N, .
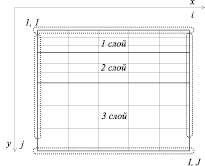
Рис. 2. Модель с направлением осей координат
Внутренний источник тепла равен поглощенному теплу и будет описываться следующим выражение [1]:
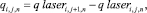(10)
где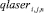 
– мощность лазерного луча в соответствующих точках координат и во времени, которая в конечно-разностном виде будет иметь вид:
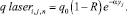(11)
Граничные условия с учетом наложенной сетки будут следующими:
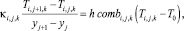(12)
где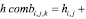 
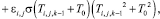
при i = 1...I, j = 1, n = 2...N;
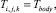(14)
при i = 1...I, j = J, n = 2...N;
при i = 1, j = 2...J – 1, n = 2...N;
при i = I, j = 2...J – 1, n = 2...N.
Начальные условия в конечно-разностном виде будут иметь вид:
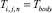(15)
при i = 1...I, j = 1...J, k = 1.
Выражения (9)–(15) представляют собой систему алгебраических уравнений, которая в общем виде будет следующей:
AT = B, (16)
где T – вектор-столбец переменных длиной M = I·J·N; A – квадратная матрица коэффициентов системы линейных алгебраических уравнений (СЛАУ) размерностью M×M; B – вектор-столбец свободных членов.
Для получения адекватного решения количество точек должно быть более тысячи (I > 10, J > 10, N > 10). Для решения СЛАУ такой размерности был использован метод Якоби [1]. Были разработаны программное обеспечение и интерфейс пользователя, окно которого представлено на рис. 3.
Результаты моделирования
На рис. 4 приведены результаты моделирования распределения температуры в биологической структуре, состоящей из эмали толщиной 20 мкм и дентина при прохождении эрбиевым (l = 2,94 мкм) и СO2 (l = 10,6 мкм) лазерами c оптическими и тепловыми параметрами, приведенными в таблице [4, 5].
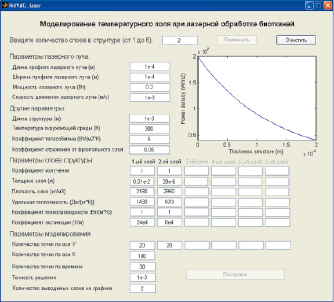
Рис. 3. Окно интерфейса программы для расчета распределения температуры
в биологических структурах
а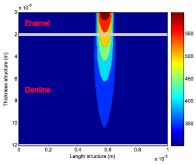
б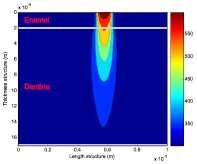
Рис. 4. Распределение температуры в структуре эмаль дентин
при обработке лазером с длиной волны l = 2,94 мкм и l = 10,6 мкм
Оптические и тепловые параметры дентина и эмали
|
C, |
k, |
ρ, |
Коэффициент отражения |
Коэффициент экстинкции, см-1 |
|||
|
l = 2,94 мкм |
l = 10,6 мкм |
l = 2,94 мкм |
l = 10,6 мкм |
||||
|
Эмаль |
970 |
1 |
2950 |
0,05 |
0,49 |
800 |
800 |
|
Дентин |
1430 |
1 |
2180 |
0,05 |
0,49 |
2400 |
540 |
Результаты моделирования совпадают с экспериментальными данными [5, 6] и показывают, что длина волны лазера существенно влияет на режим обработки биотканей, так для СO2 лазера глубина теплового проникновения в 1,5 раза больше (рис. 4), чем для эрбиевого лазера, который зачастую еще называют холодным
лазером.
Заключение
Разработанная модель, описывает процесс взаимодействия лазерного излучения с биологическими тканями и позволяет моделировать процессы лазерной обработки для различных типов лазера.
Разработанная модель на основе конечно-разностного метода и программное обеспечение на ее основе учитывает следующие особенности взаимодействия лазерного излучения с биотканями:
– сложную многослойную структуру биологических тканей;
– отражение лазерного излучения от поверхности;
– затухание лазерного луча в структуре;
– конвективную и излучательную составляющие при процессе охлаждения поверхности;
– зависимость оптических и тепловых свойств от типа ткани, входящего
в структуру.
Программное обеспечение с разработанным интуитивно понятным интерфейсом позволяет проводить численные эксперименты и рассчитывать оптимальные режимы лазерной обработки биологических структур.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации (Гос. соглашение № 14.А18.21.0126) в рамках ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы.
Рецензенты:
Рындин Е.А., д.т.н., профессор, ведущий научный сотрудник ЮНЦ РАН, г. Ростов-на-Дону;
Жорник А.И., д.ф.-м.н., профессор кафедры теоретической, общей физики и технологии ФГБОУ ВПО ТГПИ, г. Таганрог.
Работа поступила в редакцию 16.10.2012.