Известно, что источником загрязнения водных объектов является сброс сточных вод с территории промышленных предприятий с химическими производствами. Поэтому проводится контроль ее качества, прежде всего, в системах хозяйственно-питьевого водоснабжения. Методы определения показателей гидрохимического анализа, с помощью которых можно оценить качество воды, подробно рассматриваются в работе [8].
Гидрохимический анализ устанавливает состав загрязнения [1] и позволяет принять меры по снижению загрязненности. Для определения соотношений между показателями загрязнения речной воды применяется факторный анализ [3, 7].
Цель статьи – показать методику факторного анализа для изучения взаимосвязей между гидрохимическими показателями на примере результатов испытаний речной воды на загрязнение в месте водозабора реки Малая Кокшага города Йошкар-Олы.
Материалы и методы исследования
В табл. 1 приведен фрагмент данных гидрохимического и микробиологического анализа, полученных из Аналитического центра контроля качества вод МУП «Водоканал» г. Йошкар-Олы на загрязнение реки Малая Кокшага за 15 месяцев.
За период с июня 2009 по август 2010 года нами проведен поисковый анализ для выявления взаимного влияния факторов в виде показателей загрязнения речной воды. В дальнейшем с увеличением количества наблюдений можно выявить сезонные изменения параметров речной воды.
Программой наблюдений за качеством поверхностного водоисточника реки Малая Кокшага предусмотрено определение 46 параметров по физическим, бактериологическим и химическим показателям. Для факторного анализа нами отобрано 28 из-за неопределенности числовых значений показателей (напр., значения для ртути составляют < 0,00004 мг/л за весь период наблюдений).
Периодичность проведения лабораторного анализа – ежемесячно, поэтому каждая строка соответствует одной дате измерений.
Из известных методов факторного анализа (метод главных компонент, корреляционный анализ и метод максимального правдоподобия) нами применяется корреляционный анализ. При этом мы переходим на методологию эвристической, структурной и параметрической идентификации устойчивых законов [5].
Расчет описательной статистики [4] позволил установить, что по гидрохимическим показателям речной воды придется отказаться от вычисления средних арифметических значений и выявлять биотехнические закономерности [2, 3, 6, 7] по динамике загрязнения. Например, нельзя разрешать замену 15 членов ряда цветности речной воды средним арифметическим значением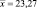 
градуса, так как не соблюдается условие допустимости коэффициента вариации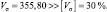 
Таблица 1
Результаты гидрохимического анализа (фрагмент) проб речной воды
|
Дата отбора проб речной воды |
Органолептические показатели: |
Обобщенные показатели: |
||||||||||
|
Цветность, градус |
Мутность, мг/л |
РН |
Сухой остаток, мг/л |
Жесткость общ, градус |
Щелочность, мг/л |
Окисляемость, мгО/л |
БПК-полное, мгО/л |
Взвешенные вещества, мг/л |
АПАВ, мг/л |
Нефтепродукты, мг/л |
Фенольный индекс, мг/л |
|
|
24.06.09 |
26 |
3,5 |
8,1 |
221 |
4,0 |
115,9 |
7,3 |
4,1 |
3,2 |
0,067 |
0,015 |
0,0006 |
|
08.07.09 |
17 |
2,4 |
8,2 |
214 |
3,6 |
109,8 |
5,5 |
2,6 |
2,1 |
0,060 |
0,015 |
0,0016 |
|
04.08.09 |
19 |
2,2 |
7,9 |
215 |
3,7 |
106,8 |
6,1 |
2,3 |
2,1 |
0,054 |
0,019 |
0,0020 |
|
02.09.09 |
18 |
1,2 |
8,0 |
229 |
4,2 |
103,7 |
6,4 |
1,3 |
1,0 |
0,052 |
0,007 |
0,0005 |
|
05.10.09 |
19 |
0,76 |
8,1 |
207 |
3,9 |
112,9 |
6,6 |
1,0 |
0,7 |
0,052 |
0,009 |
0,0005 |
|
11.11.09 |
15 |
2,2 |
7,9 |
220 |
4,0 |
106,8 |
5,1 |
2,3 |
2,5 |
0,015 |
0,010 |
0,0013 |
|
02.12.09 |
11 |
1,2 |
8,0 |
252 |
4,5 |
115,9 |
4,0 |
1,1 |
1,0 |
0,030 |
0,009 |
0,0005 |
|
20.01.10 |
10 |
2,0 |
7,6 |
280 |
4,9 |
137,3 |
4,0 |
2,1 |
3,0 |
0,024 |
0,019 |
0,0016 |
|
03.02.10 |
10 |
3,5 |
7,3 |
286 |
4,9 |
137,3 |
3,3 |
3,3 |
3,4 |
0,016 |
0,017 |
0,0007 |
|
29.03.10 |
8 |
2,2 |
7,6 |
259 |
4,6 |
131,2 |
2,9 |
2,2 |
3,0 |
0,031 |
0,017 |
0,0010 |
|
05.04.10 |
100 |
19,5 |
7,7 |
138 |
2,1 |
54,9 |
13,6 |
18,0 |
19,3 |
0,071 |
0,025 |
0,0011 |
|
05.05.10 |
27 |
5,9 |
8,3 |
192 |
3,5 |
94,6 |
5,7 |
5,9 |
5,8 |
0,060 |
0,021 |
0,0013 |
|
02.06.10 |
18 |
3,9 |
7,9 |
215 |
3,9 |
112,9 |
6,1 |
4,0 |
3,7 |
0,039 |
0,018 |
0,0008 |
|
14.07.10 |
25 |
1,2 |
7,9 |
226 |
3,7 |
112,9 |
5,6 |
1,2 |
1,2 |
0,041 |
0,013 |
0,0021 |
|
10.08.10 |
26 |
1,3 |
7,9 |
217 |
4,0 |
119,0 |
6,5 |
1,2 |
1,1 |
0,041 |
0,023 |
0,0015 |
Результаты исследования
и их обсуждение
Из 28 факторов (цветности, мутности, pH, концентрации железа, меди) составлена полная корреляционная матрица монарных (ранговых) и бинарных связей и получено 282 = 784 биотехнических закономерностей, адекватность которых показана значениями коэффициента корреляции (табл. 2).
Таблица 2
Корреляционная матрица полного факторного анализа (фрагмент)
|
Влияющие факторы x |
Зависимые факторы |
|||||||||
|
Цветность, градус |
Мутность, мг/л |
РН |
Сухой остаток, мг/л |
Жесткость общ, градус |
Щелочность, мг/л |
Окисляемость, мгО/л |
БПК-полное, мгО/л |
Взвешенные вещ-ва, мг/л |
АПАВ, мг/л |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Цветность, градус |
0,9564 |
0,9593 |
0,7414 |
0,9120 |
0,9282 |
0,8923 |
0,9645 |
0,9506 |
0,9556 |
0,7680 |
|
Мутность, мг/л |
0,9629 |
0,9428 |
0,2009 |
0,6712 |
0,7766 |
0,8133 |
0,8571 |
0,9988 |
0,9964 |
0,4572 |
|
РН |
0,0246 |
0,1600 |
0,9977 |
0,5054 |
0,3706 |
0,3524 |
0,1685 |
0,1410 |
0,2063 |
0,5890 |
|
Сухой остаток, мг/л |
0,9810 |
0,9574 |
0,8604 |
0,9482 |
0,9660 |
0,9299 |
0,9411 |
0,9500 |
0,9464 |
0,7205 |
|
Жесткость общ, град |
0,9827 |
0,9572 |
0,6824 |
0,9766 |
0,9807 |
0,9416 |
0,9257 |
0,9491 |
0,9479 |
0,7618 |
|
Щелочность, мг/л |
0,9702 |
0,9605 |
0,3349 |
0,9441 |
0,9414 |
0,9788 |
0,9107 |
0,9519 |
0,9526 |
0,7618 |
|
Окисляемость,мгО/л |
0,9868 |
0,9560 |
0,7597 |
0,9005 |
0,8937 |
0,8810 |
0,8641 |
0,9467 |
0,9335 |
0,7883 |
|
БПК-полное, мгО/л |
0,9641 |
0,9993 |
0,1382 |
0,6799 |
0,7819 |
0,8169 |
0,8592 |
0,9147 |
0,9953 |
0,4803 |
|
Взв-ые вещ-ва, мг/л |
0,9608 |
0,9966 |
0,2690 |
0,6780 |
0,7666 |
0,8047 |
0,8563 |
0,9942 |
0,9155 |
0,4314 |
|
АПАВ, мг/л |
0,7558 |
0,8430 |
0,6219 |
0,7743 |
0,7737 |
0,6523 |
0,7592 |
0,8295 |
0,8260 |
0,9922 |
|
Нефтепродукты, мг/л |
0,7740 |
0,8268 |
0,2778 |
0,5395 |
0,6851 |
0,6178 |
0,4441 |
0,7948 |
0,9113 |
0,4017 |
|
Фенол. индекс, мг/л |
0,0461 |
0,0243 |
0,0420 |
0,1310 |
0,2503 |
0,0392 |
0,0124 |
0,0309 |
0,0088 |
0,0141 |
|
Аммоний сол., мг/л |
0,9541 |
0,9588 |
0,5834 |
0,0092 |
0,1266 |
0,0973 |
0,3467 |
0,9477 |
0,9568 |
0,0377 |
|
Нитрит-ион, мг/л |
0,9593 |
0,9565 |
0,2074 |
0,6941 |
0,8097 |
0,8068 |
0,8576 |
0,9461 |
0,9549 |
0,5741 |
|
Нитрат-ион, мг/л |
0,0334 |
0,2168 |
0,5611 |
0,2251 |
0,0871 |
0,1020 |
0,1195 |
0,2047 |
0,2547 |
0,2461 |
|
Сульфат-ион, мг/л |
0,2648 |
0,4582 |
0,5398 |
0,2536 |
0,1371 |
0,0792 |
0,0788 |
0,4043 |
0,4401 |
0,3239 |
|
Фосфат-ион, мг/л |
0,4924 |
0,3039 |
0,2920 |
0,4421 |
0,4617 |
0,3356 |
0,4725 |
0,2923 |
0,2830 |
0,4949 |
|
Хлорид-ион, мг/л |
0,8304 |
0,8586 |
0,1095 |
0,6671 |
0,6559 |
0,6653 |
0,6272 |
0,8507 |
0,8531 |
0,2448 |
|
Железо, мг/л |
0,9596 |
0,9770 |
0,2370 |
0,6682 |
0,7594 |
0,7960 |
0,8563 |
0,9679 |
0,9747 |
0,4245 |
|
Калий+Натрий, мг/л |
0,6962 |
0,9762 |
0,0381 |
0,1565 |
0,0381 |
0,1555 |
0,2577 |
0,9715 |
0,9730 |
0,0172 |
|
Кальций, моль/л |
0,9899 |
0,9306 |
0,8545 |
0,9416 |
0,9342 |
0,8978 |
0,9662 |
0,9186 |
0,9193 |
0,7939 |
|
Магний, мг/л |
0,8341 |
0,9532 |
0,1997 |
0,8134 |
0,8857 |
0,8793 |
0,6806 |
0,9275 |
0,9279 |
0,4839 |
|
Марганец, мг/л |
0,0978 |
0,2673 |
0,8916 |
0,6073 |
0,4927 |
0,4705 |
0,3563 |
0,2525 |
0,3132 |
0,5362 |
|
Медь, мг/л |
0,0334 |
0,0874 |
0,4789 |
0,2757 |
0,2621 |
0,2200 |
0,2158 |
0,0147 |
0,1168 |
0,6113 |
|
Цинк, мг/л |
0,2466 |
0,2099 |
0,2206 |
0,1937 |
0,1866 |
0,1646 |
0,3738 |
0,2435 |
0,1966 |
0,4826 |
|
ОМЧ в 1 мл |
0,6622 |
0,4963 |
0,5116 |
0,6095 |
0,6550 |
0,5138 |
0,6784 |
0,4778 |
0,4480 |
0,7199 |
|
ОКБ в 100 мл |
0,7928 |
0,8101 |
0,3212 |
0,3641 |
0,7502 |
0,7013 |
0,5920 |
0,0000 |
0,7990 |
0,2223 |
|
ТКБ в 100 мл |
0,8505 |
0,8987 |
0,4094 |
0,6429 |
0,6921 |
0,7197 |
0,6475 |
0,8754 |
0,9008 |
0,1380 |
|
Сумма |
19,0629 |
19,9427 |
12,3821 |
16,2248 |
17,049 |
16,3249 |
16,6898 |
18,7474 |
19,9075 |
13,5176 |
|
Рейтинговое место |
4 |
1 |
18 |
11 |
7 |
9 |
8 |
5 |
2 |
14 |
Все эколого-химические реакции, происходящие с различными видами загрязнения в речной воде, дают по показателю концентрации одну и ту же общую математическую закономерность
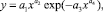(1)
где y – зависимый фактор; x – влияющий фактор; a1...a4 – параметры биотехнической закономерности (1).
Например, на мутность речной воды цветность оказывает влияние по закону экспоненциального роста (рис. 1)
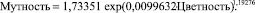(2)
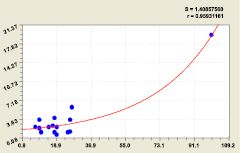
Рис. 1. Влияние цветности (абсцисса) на мутность (ордината) в речной воде
По формуле (2) минимальное содержание мутности в речной воде составляет 1,73 мг/л.
Анализ адекватности моделей выполняется сравнением фактического Fф и табличного (критического) F значений критерия Фишера [4]. Чем больше фактическое значение F-критерия, тем выше адекватность и достоверность модели.
Так, концентрация взвешенных веществ влияет на концентрацию сухого остатка в речной воде по модели (3)
Сухой остаток = 232,90014·exp(–0,00086352·взв. вещества). (3)
Табличное критическое значение критерия Фишера равно 4,67 для полученной однофакторной модели при степенях свободы для расчета фактического критерия Фишера k1 = n – m – 1 = 15 – 1 – 1 – 13 и k2 = m = 1 .
Фактическое значение критерия Фишера равно 11,12 по формулам [4]. Так как Fф = 11,12 > F = 4,67, то готовая модель (3) считается статистически досто-
верной.
Для определения наиболее сильных факторных связей, которые возникают при взаимодействии гидрохимических показателей, по связности показателей получили рейтинговые места (табл. 2).
Среди влияющих факторов по рейтингу первое место занимает кальций. На втором месте находится окисляемость и на тре-
тьем – жесткость воды. Фенольный индекс получил последнее 28-е место.
Уравнение рейтинга влияющих параметров (рис. 2) следующее:
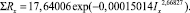(4)
Среди зависимых показателей сильные факторные связи дают мутность, взвешенные вещества и железо. Фенольный индекс также получил 28-е место.
Для оценки параметрической связности получено три критерия: количество формул, строк и столбцов, так как закономерности динамики требований к адекватности 756 формул дают снижение числа закономерностей, а также строк и столбцов корреляционной матрицы
(см. табл. 2).
Влияние принимаемого уровня адекватности на количество формул:
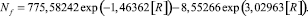(5)
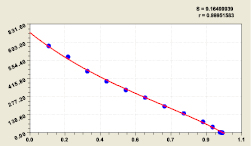
Рис. 3. Влияние принимаемого уровня адекватности на количество уравнений
С повышением требований к адекватности по росту значений допустимого уровня коэффициента корреляции [R] число оставляемых уравнений сокращается (рис. 3). При этом количество слабых факторных связей при коэффициентах [R] = 0,1...0,3 равно 284 шт.
Влияние уровня адекватности на количество строк корреляционной матрицы следующее (рис. 4):
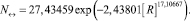(6)
Влияние уровня адекватности на количество столбцов такое (рис. 5):
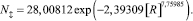(7)
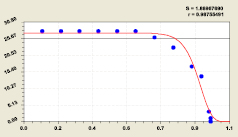
Рис. 4. Влияние уровня адекватности [R] на количество строк N↔
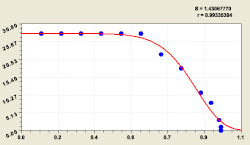
Для анализа бинарных закономерностей убрали монарные отношения между учтенными факторами по ранговым распределениям. На иерархии ранговых распределений выполняется оценка добротности исходных данных. На первом месте по добротности измерений находятся водородный показатель и магний, а на последнем – окисляемость и хлорид-ион.
Последовательно исключив клетки с малыми коэффициентами корреляции, получили бинарные закономерности, которые в наибольшей степени удовлетворяют точности гидрохимического анализа речной воды (табл. 3).
Таблица 3
Матрица параметров биотехнической закономерности (1) по сильнейшим бинарным факторным отношениям при R ≥ 0,00
|
Структура влияния |
Модель |
Коэффициент корреляции R |
|||
|
составляющая модели |
|||||
|
a1 |
a2 |
a3 |
a4 |
||
|
1. БПКn → мутность |
7,42235e-7 |
0 |
14,10434 |
0,066314 |
0,9993 |
|
2. Мутность → БПКn |
1,15036e-8 |
0 |
18,43843 |
0,046555 |
0,9988 |
|
3. Взв. вещ-ва → мутность |
8,59608e-5 |
0 |
9,45363 |
0,089816 |
0,9966 |
|
4. Мутность → взв. вещ-ва |
2,7928044e-5 |
0 |
10,61310 |
0,079639 |
0,9964 |
|
5. БПКn → взв. вещ-ва |
0,0005549 |
0 |
7,56858 |
0,11182 |
0,9953 |
|
6. Взв. вещ-ва → БПКn |
1,0092391e-5 |
0 |
11,66172 |
0,071147 |
0,9942 |
Для компактной записи выявленных биотехнических закономерностей применяется матричная форма представления (см. табл. 3). Значения расположены по убыванию коэффициента корреляции.
Приведенных шести закономерностей достаточно, чтобы составить математическую модель для расчетного обоснования. Для расширения математической модели к табл. 3 добавляются другие из моделей при R ≥ 0,95, а при необходимости – с уровня R ≥ 0,9 (сильные факторные связи).
Слабейшие факторные связи (интервал коэффициента корреляции 0,000…0,100) в частности возникают при взаимодействии с фенольным индексом, концентрациями меди, фосфат-иона, калия и натрия.
Заключение
Предложенная методика факторного анализа позволяет получить модели взаимного влияния факторов в виде показателей загрязнения речной воды. Оценка достоверности моделей проводится по критерию Фишера.
В дальнейшем при увеличении количества наблюдений факторный анализ позволит определить не только наиболее значимые факторные связи в виде биотехнических закономерностей, но и проводить мониторинг качества воды с учетом сезонной динамики гидрохимических показателей.
Рецензенты:
Воскресенская О.Л., д.б.н., профессор, зав. кафедрой экологии ФГБОУ ВПО «Марийский государственный университет»,
г. Йошкар-Ола;
Ившин В.П., д.х.н., профессор, зав. кафедрой органической химии ФГБОУ ВПО «Марийский государственный университет», г. Йошкар-Ола.
Работа поступила в редакцию 21.09.2012.