Рассмотрим дискретно - импульсную систему управления, математическая модель которой описывается семейством уравнений
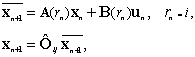 (1)
(1)
где ![]() n-мерный вектор состояния объекта;
n-мерный вектор состояния объекта; ![]() k-мерный вектор управления;
k-мерный вектор управления; ![]() s-мерный вектор выхода объекта;
s-мерный вектор выхода объекта;![]() однородное дискретное состояние цепи Маркова, описывающее процесс смены режима объекта на множестве
однородное дискретное состояние цепи Маркова, описывающее процесс смены режима объекта на множестве ![]() и матрицей вероятностей перехода
и матрицей вероятностей перехода ![]() от режима
от режима ![]() до режима
до режима ![]() . Матрицы
. Матрицы ![]() известные матрицы соответствующих размеров.
известные матрицы соответствующих размеров. ![]()
![]() постоянная матрица, такая, что
постоянная матрица, такая, что ![]() ; эти матрица описывает импульсное изменение вектора состояния объекта управления в момент смены режима
; эти матрица описывает импульсное изменение вектора состояния объекта управления в момент смены режима ![]() на
на ![]() .
.
Будем предполагать, что вектор выхода ![]() и процесс смены режима
и процесс смены режима ![]() доступны наблюдению.
доступны наблюдению.
Рассмотрим линейное управление со статической обратной связью по выходу объекта, синхронно переключаемой со сменой режима:
![]() если
если ![]() (2)
(2)
такое, что для каждого фиксированного ![]() выражение (2) стабилизирует управление для детерминированной системы
выражение (2) стабилизирует управление для детерминированной системы
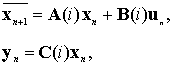
или, другими словами, такое, что матрица
![]() (3)
(3)
является матрицей, собственные значения которой лежат в левой полуплоскости.
Матрица ![]() может быть получена при помощи известных методов решения проблем управления с детерминированной статической обратной связью по выходу.
может быть получена при помощи известных методов решения проблем управления с детерминированной статической обратной связью по выходу.
Получим условия, которым должны удовлетворять управление (2), чтобы обеспечить стабилизацию в среднем квадратическом системы (1). Такое управление назовем робастным стабилизирующим.
Условия существования стабилизирующего управления с обратной связью по состоянию, т. е. такого управления (2) при котором определить единственное стационарное распределение Марковской цепи ![]() в пространстве
в пространстве ![]() , относительно которого существует момент второго порядка можно определить теоремой.
, относительно которого существует момент второго порядка можно определить теоремой.
Теорема. 1. Пусть матрица ![]() положительно полуопределенная матрица, а матрица
положительно полуопределенная матрица, а матрица ![]() положительно определена и
положительно определена и ![]() . Тогда, если положительно определенная матрица
. Тогда, если положительно определенная матрица ![]()
![]() удовлетворяет уравнению
удовлетворяет уравнению
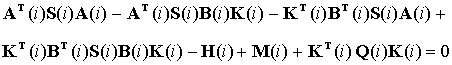
где ![]() , то линейное управление со статической обратной связью по выходу объекта (2), определяемое формулой
, то линейное управление со статической обратной связью по выходу объекта (2), определяемое формулой
![]()
является робастным стабилизирующим управлением в среднем квадратическом.
Стабилизация в среднем квадратическом является основной проблемой данной работы. Рассмотрим дополнительно следующую теорему, использующую условия стабилизации системы (1) в среднем квадратическом.
Теорема 2. Если система (1) стабилизируема в среднем квадратическом, то найдутся такие матрицы ![]() и
и ![]() , что для них выполнено неравенство
, что для них выполнено неравенство
![]()
Обозначим
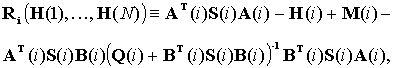
где ![]() и
и ![]() .
.
Тогда для данных систем можно получить следующие теоремы:
Теорема 3. Если ![]() решение уравнения
решение уравнения ![]() , а
, а ![]() решение неравенства
решение неравенства ![]() при условии, что
при условии, что ![]() , то
, то ![]() .
.
Рассмотрим множества ![]()
множество решений уравнения ![]() и
и ![]() множество решений неравенства
множество решений неравенства ![]() .
.
Теорема 4. Множество
![]()
не пусто, если не пусто множество
![]()
и решение ![]() также принадлежит множеству
также принадлежит множеству ![]() .
.
Вывод
Для линейной дискретной системы случайной структуры со скачкообразным изменением вектора состояния объекта в момент смены режима получены условие, когда линейное управление со статической обратной связью по выходу объекта, является робастным стабилизирующим управлением по отношению по норме неопределенностям, удовлетворяющим условию (2).
СПИСОК ЛИТЕРАТУРЫ:
- Pakshin P.V. Robust output feedback of nonlinear systems with random jumps // Proceedings of the 15th World Congress of IFAC. Barcelona. 2002. (CD ROM).
- De Souza C.E. and Fragoso M.D. control for linear systems with Markovian jump parameters // Control-Theory and Advanced Technology. 1993. V.9. P. 457-466.
- Boyd S., El Ghaoui L., Feron E. and Balakrishnan V. Linear matrix inequalities in control and system theory. Philadelphia.: SIAM, 1994.
- Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука, 2002.



