В связи с большими изменениями в системе высшего образования появился интерес к моделированию учебного процесса [1] и управлению динамикой этого процесса [2]. В данной статье построены и исследованы математические модели распространения знаний и управления процессом обучения в студенческой среде с учетом уровня квалификации преподавателей.
Разделим множество обучаемых студентов на три группы. К первой группе отнесем сильных по успеваемости студентов, ко второй - средних и к третьей группе – слабых студентов. Это распределение условное, оно не отражает степени одаренности, начальной подготовки, трудолюбие, мотивировку. Однако исследование даже такой простой модели позволяет получить интересные качественные результаты.
В первой модели будем считать, что знания равномерно распределены в каждой из групп.
Обозначим через Ni(t), i = 1,2,3 уровень знаний в студенческой среде в i-й группе, Ui(t), - управляющее воздействие на i-ю группу. Управляющее воздействие может быть непрерывным, дискретным (контрольные мероприятия), или смешанного типа. Введем коэффициенты: αi - коэффициент усвоения знаний в i-й группе, βi- коэффициент забывания учебного материала, δi - коэффициент управляемости i-ой группой, εi- коэффициент управляемости i-ой группой в зависимости от уровня квалификации преподавателя, γij - коэффициент влияния i-ой группы на j-ю. В результате получаем простейшую модель:
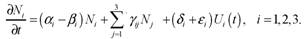 (1)
(1)
В качестве начальных условий берется начальная подготовка группы. Σ означает суммирование по i ≠ j.
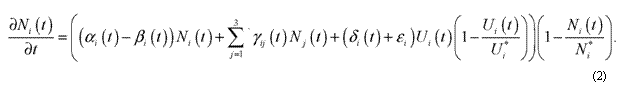
Начальные условия такие же, как в модели (1).
В моделях (1) и (2) предполагалось, что знания распределены внутри группы равномерно. Откажемся от этого предположения, полагая, что распространение знаний происходит по параметру r. Для самого сильного студента r = 0 Тогда модель выглядит следующим образом:
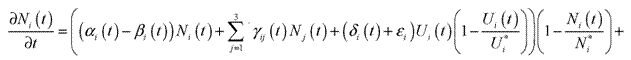
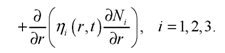 (3)
(3)
Здесь ni(r,t) - коэффициент передачи знаний в i-й группе. В качестве начальных значений в модели (3) берется уровень начальной подготовки.
Рассмотрим динамику образовательных процессов, полученных при численной реализации моделей (1)-(3). В простейшей модели (1) Ni(t) (i = 1,2,3) показывает уровень знаний студентов i-й группы в момент времени t. Если обозначить коэффициенты αi - βi = ki то модель примет вид:
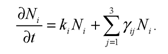 .
.
Эту систему можно записать так
где  .
.
Решение этой системы следует искать в виде
![]()
где λi -характеристические числа матрицы A , Pij -координаты собственных векторов. Фундаментальная система решений имеет вид:
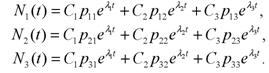
Постоянные интегрирования C1,C2,C3 находятся из условия Ni(0) = Nio- исходный объем знаний в начале обучения. Меняя коэффициент управляющего воздействия δi, получим различные картины поведения системы.
Рассмотрим динамику процесса образования с учетом насыщения. Об этом явлении написано в работе [1]. Введем еще одно обозначение:
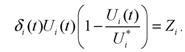
Модель (2) примет вид
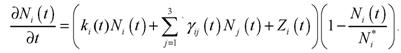
![]()
Решение ищем в виде :
![]()
Данную систему дифференциальных уравнений целесообразно решать методом повышенной точности - методом Рунге-Кутта. Решение показывает, что все три группы студентов достигают определенного предела уровня знаний и происходит процесс насыщения.
Сравнивая результаты реализации моделей (1) и (2), можно заметить, что в первом случае объем знаний неограниченно растет, а во второй модели происходит процесс насыщения и объем знаний не превосходит определенного предела. Такая картина более реальная и поэтому целесообразно использовать модель (2).
СПИСОК ЛИТЕРАТУРЫ:
1. С.П. Капица, С.П. Курдюмов, Г.Г. Мали-нецкий. Синергетика и прогнозы будушего. Изд-во Едиториал УРСС, 2003г., 288с.
2. И.В. Бойков, И.А. Суздалева. Об одной модели образования. Труды Средневолгжского математического общества. Саранск №5, 2006г. С. 229-234.



