Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Наибольшие перспективы современного естествознания в последние годы связаны с бурным и успешным развитием синергетики и приложением ее результатов к различным областям науки [1,2]. Синергетические математические модели различных биологических объектов, как нелинейных открытых детерминированных систем, заставляют пересмотреть методы анализа и таких привычных для медицинской практики процессов, как изучение динамики артериального давления. Появившиеся новые медицинские технологии позволяют проводить долговременные мониторинговые исследования, в которых (в отличие от обычных медицинских исследований) получаемые ряды данных уже не являются статистически независимыми и не описываются классической статистикой. Обработка и анализ результатов длительных мониторингов  требует развития новых статистических и математических методов в условиях априорной неполноты и неопределенности наблюдаемых временных рядов [3,4].

Это позволяет обнаружить скрытые периодичности и синергетические особенности функционирования организма, которые могут полностью переосмыслить наше представление о хроноструктуре адаптационного процесса.

Материал и методы

7-суточная/24-часовая регистрация АД была проведена с помощью неинвазивного амбулаторного автоматического аппарата для регистрации АД (ТМ2421; A&D Co., Япония). Прибор был настроен так, чтобы снимать данные с 30-минутными интервалами с 6:00 до 22:00, и с 60-минутными интервалами с 22:00 до 6:00. Испытуемые были проинструктированы о том, что они должны  соблюдать обычный распорядок дня и не должны двигать рукой в момент регистрации АД.

В работе анализировались данные измерений среднего артериального давления (MAP) четырех испытуемых, а именно, двух молодых мужчин 24 и 34 лет, мужчины возраста 54 лет и женщины
57 лет. Среднее артериальное давление выбиралось из соображений снижения удельного веса флуктуационной компоненты первичных рядов данных и выявления наиболее общих закономерностей функционирования с целью построения автоматизированного математического прогноза.

На основе статистической обработки измерительной информации выявлялись общие закономерности процесса MAP для всех четырех испытуемых и характерные особенности, определяемые возрастом пациента. Нахождение закономерностей, тенденции в поведении MAP позволяет построить математическую модель, которая используется для оценки его будущего значения. Отдельно рассматриваются особенности построения краткосрочного и долгосрочного прогнозов для мониторинговых рядов данных, а также выбор оптимальной модели в условиях переменной длины ряда данных.

1. Анализ динамики (MAP) с помощью процедуры 9-точечного сглаживания

Анализ данных измерений показывает, что динамика MAP характеризуется не только циклической структурой с периодом 24 часа, но и флюктуирующей составляющей [5-8]. Для первичной качественной и количественной оценки закономерностей динамики исследуемого процесса, чтобы выделить тенденцию изменения  MAP по данным флюктуирующих измерений  была использована процедура 9-точечного сглаживания. Сглаженное значение величины MAP в каждой j-й точке определяется как взвешенная сумма 9 последовательных измерений с центром в текущей точке. При этом крайние (первое и девятое измерения) учитываются с весом вдвое меньшим, чем остальные 7 измерений.

Если p_j измеренное значение MAP в момент времени j, то 9-точечное сглаженное среднее в этот момент времени определяется выражением

Получены 9-точечные сглаженные значения  для 4-х исследуемых испытуемых и измеренные значения . Изменение MAP на интервале  характеризуется "двугорбой" формой графика зависимости сглаженного среднего  от времени. MAP к середине этого интервала резко убывает, а затем опять возрастает к концу интервала. Такой характер изменения MAP проявляется  во всех суточных циклах, что дает основания считать этот процесс закономерным.

Указанные закономерности в значительной мере проявляются в характере изменения MAP для людей старшего возраста. Так, фаза падения MAP для 54-летнего испытуемого завершается около 4 часа утра. Время окончания фазы падения 57-летней испытуемой приходится на интервал времени от позднего вечера до раннего утра.  На интервале  также во многих циклах наблюдается снижение MAP к середине интервала MAP с последующим ростом к концу интервала. Тем не менее, характер изменения MAP для этой возрастной группы носит значительно менее регулярный характер, чем для молодых испытуемых. Это проявляется в скачкообразном изменении максимумов, более значительными колебаниями интервала , высоким разбросом величины изменения MAP в течение фазы падения и продолжительности этой фазы, менее монотонным характером  изменения MAP в фазе подъема и снижения.

Из статистической оценки основных характеристик динамики сглаженных значений MAP для исследуемых пациентов (математического ожидания (МО), стандартного отклонения (СО) последовательности максимальных значений максимумов, обозначенных соответственно M_max, σ_max; МО и СО последовательности интервалов , обозначенных M_int,  σ_int ; МО времени окончания фазы роста t_k1, и начало фазы падения t_k2, обозначенных M_t1 и M_t2; МО и СО последовательности минимумов и МО времени t_{k min} их наступления, обозначенных M_min, σ_min, M_{t min}; МО и СО величины изменения MAP на интервале времени (t_k2; t_{k min}) от максимума до минимума), обозначенных M_Δ, σ_Δ; МО и СО продолжительности фазы падения, обозначенных M _tΔ, σ _tΔ, ) видно, что в оценках математических ожиданий практически не проявляются закономерности, определяемые возрастом пациентов за исключением M_max, имеющим некоторую тенденцию к увеличению с возрастом. Продолжительность интервалов времени  между максимумами составляет 5 - 7 часов, причем первый и второй максимумы для молодых испытуемых наблюдается на  2-3 часа позже, чем для испытуемых старшего возраста. Однако малая выборка пациентов не дает достаточных оснований считать этот сдвиг во времени интервала  закономерным.

Степень рассеивания исследуемых   параметров, определяемая стандартными отклонениями, значительно более высокая для испытуемых старшего возраста, чем для молодых. Стандартные отклонения всех параметров, за исключением σ_min для испытуемых старшего возраста больше, чем соответствующие стандартные отклонения у молодых и в ряде случаев превышают их больше, чем в два раза. Большие значения СО обусловлены значительно более высокой изменчивостью исследуемых параметров для исследуемых старшего возраста.

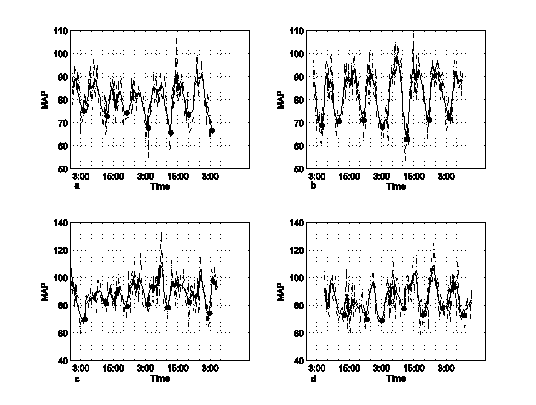
Рис. 1. Измеренные значения MAP (пунктирная линия) и 9-точечные сглаженные средние MAP (сплошная линия)  для 4-х исследуемых пациентов: a) 24 года; b) 34 года; c) 54 года; d) 57 лет

Таблица 1. Статистические оценки основных характеристик динамики MAP

Относительно невысокая степень рассеивания максимальных значений MAP для молодых испытуемых (σ_max <3) позволяет удовлетворительно оценивать будущие значения максимумов MAP. Если в качестве прогнозируемого значения следующего максимума выбрать известное значение текущего максимума, то СО такого прогноза определяются значениями σ_max.

2. Долгосрочное прогнозирование MAP методом аппроксимации исходных данных периодической функцией

Регулярный характер изменения MAP открывает дополнительные диагностические возможности оценки сердечно-сосудистой системы. На основании информации, полученной при измерении АД в течение недели, можно выполнять долгосрочное прогнозирование (до 1/2 от длины имеющегося ряда исходных данных), если за интервал времени, на который выполняется прогнозирование, никаких чрезвычайных сбоев функционального состояния организма не происходит [7].

С целью реализации долгосрочного прогноза (в рассматриваемом случае - на несколько суток и более) циклическая кривая MAP была аппроксимирована периодической функцией

.

Здесь  , φ - начальная фаза, определяемая временем суток начала измерения. Такая аппроксимация не учитывает колебания давления на интервале (t_k1; t_k2), точная экстраполяция которого на длительное время представляется весьма проблематичной, но в то же время дает представление о среднем значении MAP на этом интервале.

Для каждого из исследуемых пациентов оценивание неизвестных параметров A и B, а также уточнение начальной фазы φ выполнялось  таким образом, чтобы обеспечить минимум среднеквадратической ошибки аппроксимации по первым 100 точкам измерений для каждого пациента. Построенные на основе оцененных значений A и B аппроксимирующие функции были использованы для экстраполяции данных всех остальных точек (j > 100).

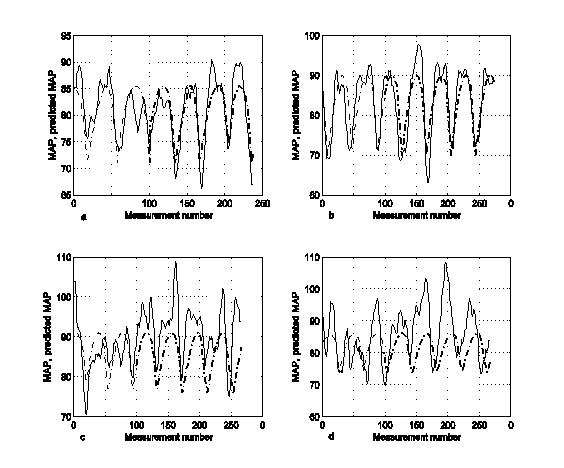
Рис. 2. 9-точечные сглаженные средние MAP (сплошная линия) и экстраполированные значения MAP при j>100 (жирная пунктирная линия) для 4-х исследуемых пациентов: a) 24 года; b) 34 года; c) 54 года; d) 57 лет

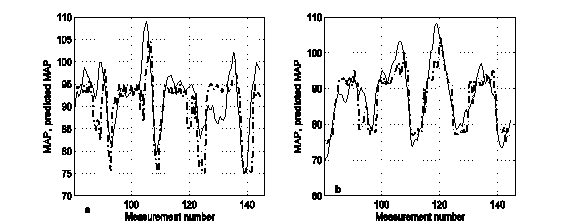
Рис. 3. 9-точечные сглаженные средние MAP (сплошная линия) и экстраполированные на 3 часа значения MAP при j>100 (пунктирная линия) для 2-х пациентов старшего возраста: a) 54 года;  b) 57 лет

Показано, что точность прогноза для молодых пациентов существенно выше, чем для пациентов старшего возраста. Для пациентов старшего возраста преобладают большие ошибки экстраполяции  и диапазон их ошибок шире, чем для молодых пациентов.

Для молодых пациентов, динамика MAP которых имеет более регулярный характер, долговременный прогноз характеризуется в большинстве случаев высокой точностью. Для MAP 24-летнего пациента в 92-х из 138 точек (67%) ошибка экстраполяции меньше 3 единиц, для 34-летнего пациента эта точность достигается в 54%. Однако для пациентов старшего возраста вероятность относительно точного прогноза значительно уменьшается (для 54-летнего пациента - 14%, для 57-летней пациентки - 19%). Закономерности поведения MAP таких пациентов не так очевидны и для долгосрочного прогноза требуется проведение специальных исследований.

Таблица 2.  Характеристики точности долговременного прогноза MAP

3. Краткосрочное прогнозирование MAP пациентов старшего возраста на основе стохастической модели

Величина интервала времени, на которое производится прогнозирование, и цель прогнозирования  оказывают влияние на выбор модели, являющейся основой для оценки текущих и будущих значений исследуемого процесса изменения MAP по данным искаженных помехами измерений.

Для краткосрочного прогнозирования MAP пациентов старшего возраста, когда ограничены возможности обосновать закономерности длительного развития процесса, предлагается использовать стохастическую модель. Исходя из периодического характера изменения MAP, рассмотренного в п.2, детерминированная основа модели представляется периодической функцией

Здесь p_j- действительное значение MAP, t_j- время j-о измерения, ,  φ- начальная фаза, определяемая временем суток начала измерения. Величины A, B и φ оценивались аналогично предыдущему, исходя из минимизации среднеквадратической ошибки аппроксимации по первым 100 измерениям MAP.

В пространстве состояний [2] детерминированная основа модели записывается следующим образом

.

Здесь нелинейная функция  имеет вид

 ,

где знак "+" используется, если , а  знак "-", если

Непредсказуемые изменения процесса учитываются введением в уравнение модели стохастической составляющей  с неизвестными статистическими свойствами.

Таким образом, уравнение состояния имеет вид

                                          (1)

Уравнение измерения MAP определяется следующим образом

.                                                           (2)

Здесь  - последовательность случайных ошибок измерения MAP.

Оценка прогнозируемого следующего измерения и оценка текущего значения MAP(фильтрация) на основе модели (1,2) выполняется следующим образом. Начальное значение фильтрованной оценки  выбирается равным первому измеренному значению MAP

.

После этого с помощью блоков экстраполяции и фильтрации для последующих моментов времени t_j (j=2,3,...) определяются:

• экстраполированное на момент времени значение MAP

,

• фильтрованное в момент времени t_j значение MAP путем корректировки экстраполированного значения  на величину его отклонения от измеренного значения 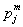, умноженного на коэффициент K=0.3.

.

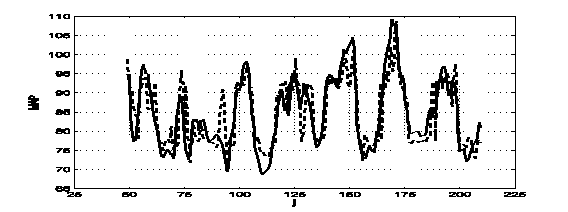
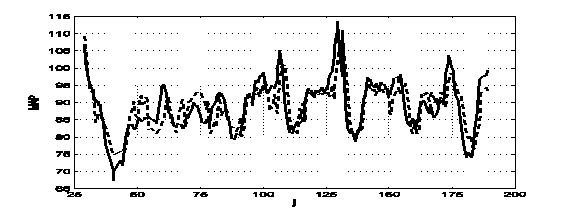
Рис. 4. Экстраполированные (пунктирная кривая) и сглаженные (сплошная кривая) значения MAP 57-летней (верхний рисунок)  и 54-летнего (нижний рисунок) обследуемых

Выбор постоянного значения коэффициента K обеспечивает увеличение веса каждого последующего измерения по экспоненциальному закону, и таким образом, повышение скорости реагирования алгоритма на отклонения процесса от модели [5].

Использование алгоритма фильтрации для краткосрочного прогноза MAP пациентов старшего возраста позволяет существенно повысить точность прогнозирования по сравнению с прогнозом на основе предварительного выбора аппроксимирующей функции. Для MAP 54-летнего пациента в 74-х из 161 точек (46%) ошибка экстраполяции меньше 3 единиц, для 57-летней испытуемой эта точность достигается в 81 из 162 точек (50%).

4. Математическое моделирование изменений МАР, как совокупности детерминированных и случайных величин

Итак, для старшей возрастной группы обследуемых характерна значительно более высокая вариабельность, скачкообразность изменения МАР, во-первых, из-за непредсказуемых сбоев, обусловленных, возрастными нарушениями процессов регуляции систем организма, и во-вторых, усложнения картины релаксационных процессов из-за увеличения жесткости сосудов. Это дает основания рассматривать изменения МАР для старшей возрастной группы, как существенно стохастический процесс. И позволяет формировать математическую модель на основе представления процесса изменения МАР через совокупность детерминированных и случайных величин, статистические характеристики которых априорно неизвестны и подлежат идентификации по данным наблюдений.

В качестве детерминированной основы модели может быть использовано уравнение (1), которое в рекуррентной форме записывается следующим образом

.

Здесь нелинейная функция  имеет вид

 ,

где знак "+" используется, если , а  знак "-", если

Непредсказуемые изменения процесса учитываются введением в уравнение модели стохастической составляющей .

Таким образом, модель изменения MAP в пространстве состояний имеет вид

,                                              (1.а)

где  - некоррелированная последовательность с нулевым математическим ожиданием и неизвестной дисперсией .

Предполагая, что измерения MAP выполняются в присутствии аддитивных шумов, представим уравнение измерения MAP следующим образом

,                                         (2)

где z_i - измеренное значение MAP, η_i - некоррелированная последовательность случайных ошибок измерения MAP с нулевым математическим ожиданием и неизвестной дисперсией .

Для идентификации неизвестных дисперсий σ_ξ²  и  по данным измерений сформируем следующие последовательности

,                                          (3)

.                              (4)

С учетом выражений (1), (2) представим измерения z_j в следующем виде

.

Раскладывая в ряд Тейлора первого порядка функцию  в окрестности точки  получим .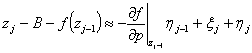

Тогда математическое ожидание последовательности                                                          

,                                                           (5)

где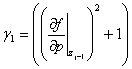

Используя выражения (1), (2) представим  следующим образом

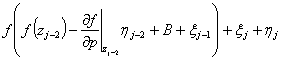Раскладывая в ряд Тейлора первого порядка функцию  в окрестности точки , а функцию  в окрестности точки  получим

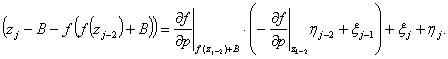
Тогда математическое ожидание последовательности  

,                                                    (6)

где ,   .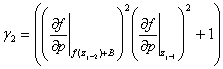

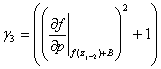Решая систему (5),(6) двух линейных уравнений с двумя неизвестными σ_ξ² и σ_η², получим

,                                             (7)

.                                                   (8)

Математические ожидания последовательностей B_1,j и B_1,j могут быть оценены путем статистического усреднения их наблюдаемых значений

, .

Тогда оценки неизвестных дисперсий шумов модели (1),(2) определяются в соответствии с выражениями (7), (8), в которых вместо E(b_1,j) и  E(B_2,j) используются их оценки.

Алгоритм прогнозирования МАР включает в себя следующие этапы.

1. Оценивание параметров A, B и φ, исходя из минимизации среднеквадратической ошибки аппроксимации по первым N измерениям MAP.
2. Идентификация неизвестных дисперсий σ_ξ² и σ_η², характеризующих степень рассеяния самого процесса MAP и его измерений.
3. Построение обобщенного адаптивного фильтра Калмана для прогнозирования MAP с использованием полученных оценок дисперсий вместо неизвестных истинных значений.

На основе описанного алгоритма выполнялся прогноз MAP для обследуемых старшего возраста. Оценки параметров A, B и φ и неизвестных дисперсий σ_ξ² и σ_η²  выполнялись по данным первых 100 измерений MAP (N=100). Для 54-летнего обследуемого определены следующие оценки среднеквадратических отклонений шумов σ_ξ=3.7 и σ_η=4.6 и , для 57-летней обследуемой  -  σ_ξ=6.2 и σ_η=5.6 и . Прогнозируемые на 3 часа значения MAP сравнивались с их сглаженными значениями. Сглаженное значение величины MAP в каждой j-й точке определялось как взвешенная сумма 7 последовательных измерений с центром в текущей точке. При этом крайние (первое и седьмое измерения) учитывались с весом вдвое меньшим, чем остальные 5 измерений. 

Использование адаптивного обобщенного фильтра Калмана, основанного на идентификации неизвестных дисперсий шумов модели обеспечивает высокую эффективность краткосрочного прогноза MAP  пациентов старшего возраста. Для MAP 54-летнего пациента в 90-х из 168 точек (54%) ошибка экстраполяции меньше 3 единиц, для 57-летней испытуемой эта точность достигается в 88 из 169 точек (52%).

Заключение

1. Статистическая обработка данных измерений среднего артериального давления, основанная на формировании
9-точечного сглаженного среднего, позволила выявить ряд обобщенных закономерностей его динамики. Показано, что динамика MAP имеет циклический характер с периодом в 24 часа, минимумы достигаются в 3-5 часов утра. В области больших значений MAP, которые имеют место в дневное время, характерным является наличие двух максимумов. Интервалы времени между максимумами составляют 5-7 часов. Характер изменения MAP для старшей возрастной группы носит значительно менее регулярный характер, чем для молодых пациентов. Это  проявляется в скачкообразном изменении максимумов, более значительными колебаниями интервала между максимумами, высоким разбросом величины изменения MAP в течение фазы падения и продолжительности этой фазы, менее монотонным характером изменения MAP в фазе подъема и снижения.

2. Регулярный характер изменения MAP у молодых пациентов позволил выполнить долгосрочное прогнозирование на несколько суток и более на основании выбора параметров периодической аппроксимирующей функцией по данным начальных измерений. Показано, что для молодых пациентов долговременный прогноз характеризуется в большинстве случаев высокой точностью. Для MAP 24-летнего пациента в 92-х из 138 точек (67%) ошибка экстраполяции меньше 3 единиц, для
34-летнего пациента эта точность достигается в 54%. Однако для пациентов старшего возраста вероятность относительно точного прогноза значительно уменьшается (для 54-летнего пациента - 14%, для 57-летней пациентки - 19%). Закономерности поведения MAP таких пациентов не так очевидны и для долгосрочного прогноза требуется проведение специальных исследований.

3. Поэтому следующим шагом в построении краткосрочного прогнозирования (несколько часов) MAP пациентов старшего возраста, когда ограничены возможности обосновать закономерности длительного развития процесса, предлагается использовать алгоритмы фильтрации и экстраполяции на основе стохастической модели процесса. Показано, что алгоритм краткосрочного прогнозирования MAP пациентов старшего возраста обеспечивает повышение точности по сравнению с прогнозом на основе предварительного выбора аппроксимирующей функции. Прогнозирование на основе предложенного алгоритма приводит к ошибке в половине случаев не превышающую 3 единиц.

4. Для обобщенного случая составления прогноза для пациентов любого возраста, предложен алгоритм адаптивного прогнозирования артериального давления, основанный на формировании совокупной стохастической модели процесса его изменения с априорно неизвестными дисперсиями шумов модели и идентификации неизвестных дисперсий. Минимизированные эндогенные особенности и характерная амплитудная, временная устойчивость организма, а также и устойчивость по управляющим функциям, позволяет разработать автоматизированный прогноз оценки текущих физиологических параметров. Показано, что обобщенный адаптивный фильтр Калмана, использующий идентифицированные оценки дисперсий вместо их истинных значений, обеспечивает достаточно хорошую точность краткосрочного прогнозирования артериального давления даже для пациентов старшего возраста. Использование обобщенной модели на основе представления процесса изменения МАР через совокупность детерминированных и случайных величин, статистические характеристики которых априорно неизвестны и подлежат идентификации по данным наблюдений, позволяет строить автоматический математический краткосрочный и долгосрочный прогнозы текущего состояния пациентов по данным медицинского мониторинга любой временной выборки.

5. Обнаруженные скрытые периодичности и синергетические особенности функционирования организма, проявляющиеся в усилении стохастической компоненты у обследуемых более старшего возраста, могут полностью переосмыслить наше представление о хроноструктуре адаптационного процесса.

СПИСОК ЛИТЕРАТУРЫ:

1. Капица С.П., Курдюмов С.П., Малинецкий Г.Г. Синергетика и прогнозы будущего. - М.: УРСС, 2004.
2. Чернавский Д.С. Динамическая теория информации. - М.: УРСС, 2004.
3. Сейдж Э., Мелс Дж. Теория оценивания и ее применение в связи и управлении. - М.: Связь, 1976. - 494 с.
4. Рагульская М.В. // Синергетические аспекты поведения биологических систем при воздействии непороговых внешних полей. Биомедицинские технологии и радиоэлектроника. - 2005. - №1-2. - С. 3 - 12.
5. Чибисов С.М., Стрелков Д.Г., Халберг Ф. Диагностическое значение долгосрочного мониторирования артериального давления при различной ситуационной обстановке // Буковинський медичний вiсник, Чернiвцi, Украина, 2006, №4, с.192-193.
6. Чуев Ю.В., Михайлов Ю.Б., Кузьмин В.И. Прогнозирование количественных характеристик процессов. - М.: Советское радио, 1975. - 400 с.
7. Halberg F., Chibisov S., Radysh I., Cornelissen G., Bakulin A. Time structures (chronomes) in us and around us // Monography. - Moscow: PFUR, 2005. - 186 p.
8. Бреус Т.К., Чибисов С.М., Баевский Р.М., Шебзухов К.В. Хроноструктура ритмов сердца и факторы внешней среды. - М.: Изд-во РУДН; Полиграф сервис, 2002. - 232 с.