Актуальность работы. В последние годы широкое развитие получили технологии реабилитационного лечения психосоматических заболеваний, основанные на использовании биологической обратной связи. Среди них успешно применяется и биоуправляемый игровой тренинг для коррекции стрессиндуцированных состояний у лиц опасных профессий, в спортивной практике, для лечения психосоматических заболеваний, а также для реабилитационного лечения детей, страдающих синдромом гиперактивности и дефицита внимания [1].
В процессе проводимого биоуправляемого игрового тренинга постоянно сохраняется необходимость оценки объективного состояния ведущих физиологических систем организма пациента в режиме on line [2, 3]. В задачах диагностики в режиме on-line целесообразно использовать быстрые интеллектуальные системы. К ним, прежде всего, относятся искусственные нейронные сети (ИНС) [4].
При этом актуальным является проведение исследований, связанных с клинической оценкой эффективности этих алгоритмов с использованием критериев чувствительности и специфичности.
Работа выполнена при поддержке проекта РНПВШ.2.2.3.3/4307 и в соответствии с планами проблемной комиссии по хронобиологии и хрономедицине РАМН и научным направлениям медицинского факультета БелГУ «Разработка универсальных методологических приемов хронодиагностики и биоуправления на основе биоциклических моделей и алгоритмов с использованием параметров биологической обратной связи».
Цель и задачи исследования. Целью является оптимизация диагностических исследований распознавания степени активности автономной нервной системы у здоровых лиц, находящихся в различных функциональных состояниях.
Для достижения поставленной цели необходимо решить следующие задачи:
- разработать модель двухслойной прямонаправленной искусственной нейронной сети;
- сформировать обучающий алгоритм с использованием обратного распространения ошибки;
- разработать клинические критерии эффективности алгоритмов распознавания состояния активности автономной нервной системы по показателям чувствительности и специфичности.
Методы исследования
Включают использование системного анализа с декомпозицией целей и функций разрабатываемой системы, моделированием рассматриваемых функциональных состояний и степени активности автономной нервной системы.
Основное содержание работы
Известно, что регулирование параметров, избранных для мониторинга при биоуправлении, в обычных условиях реализуется за счет сочетанной деятельности нескольких координирующих и пусковых иерархических систем. На основе информационного анализа нами ранее было разработано модельное представление об иерархии управления регуляцией частотой сердечных сокращений, включающей шесть режимов:
1) детерминированный;
2) квазидетерминированный;
3) гармонический;
4) квазигармонический;
5) квазистохастический;
6) стохастический.
Математические модели, предложенные нами, позволяют, во-первых, выделить и прогнозировать динамику того или иного параметра, относящегося к механизмам регуляции ЧСС в условиях перманентного воздействия извне, а во-вторых, определить характер смены динамических режимов, а следовательно и функциональных состояний, им соответствующих.
Для решения поставленных задач была использована методология системного анализа, теория управления и теория моделирования. Прежде всего, были разработаны составляющие компоненты модели микроструктурных паттернов вариабельности ритма сердца (HRV).
Составляющие компоненты микроструктурной модели паттерна HRV включают вектор повторяющихся значений предыдущего и последующего межпульсовых интервалов, временную составляющую из нулевых, укорачивающих и удлиняющих коррекций межпульсовых интервалов. Алфавит системы всегда постоянен и включает все классы дифференциальной гистограммы распределения паттерна HRV, включающие норму, тахи- и брадиритмию.
Данная модель рассматривается нами в виде последовательного развертывания цепи событий, имеющих условно-вероятностный характер. В соответствии с ним строят дифференциальную кривую распределения, а по ее вероятностям вычисляют все параметры энтропии. Вычисления осуществляли в основной выборке по 500 кардиоинтервалов: всю полученную шкалу длительностей межпульсовых интервалов делили на классовые интервалы по 0,05 с и каждый интервал временного ряда регистрируемого вектора кодировался номером классового интервала, соответствующего его длительности.
Информационные показатели модели соответствуют параметрам энтропии ритма сердца. Функциональные показатели модели характеризуются формулами вычисления параметров энтропии ритма сердца, каждый из которых характеризует ту или иную меру процесса. В частности, нормированная энтропия HN отражает степень активности автономной нервной системы (АНС). Нормированная энтропия вычисляется в виде отношения фактической энтропии к двоичному логарифму числа 500 (HN = (-ΣPilog2Pi)/log2500.
В заключительной экспериментальной части работы были проведены исследования на адекватность разработанных моделей реальным электрофизиологическим процессам.
Для этих целей были проанализированы 189 записей межпульсового интервала у 94 практически здоровых студентов Белгородского государственного университета. Все они входили в одну социальную и возрастную группу от 17 до 24 лет.
Обучающая выборка включала 139 записей у 69 человек. В экзаменационную выборку входили 25 человек, у которых были проанализированы 50 записей межпульсового интервала.
В результате были получены шесть классов нормированной энтропии, которые соответствовали известным функциональным состояниям и дифференцированной степени активности автономной нервной системы (АНС) человека:
- РВП СНС (Резко выраженное преобладание симпатической нервной системы);
- ВП СНС (Выраженное преобладание симпатической нервной системы);
- УП СНС (Умеренное преобладание симпатической нервной системы);
- НОРМА (Равновесное состояние между симпатикусом и парасимпатикусом);
- УП ПСНС (Умеренное преобладание парасимпатической нервной системы);
- ВП ПСНС (Выраженное преобладание парасимпатической нервной системы).
В нашем исследовании вычисленная нормированная энтропия использовалась для формирования мнения эксперта и целевых выходных векторов нейронной сети.
Метод поставленной выше задачи классификации уровней иерархии управляющих систем на основе диагностики степени активности вегетативной нервной системы может базироваться на моделировании как однослойной сети прямого распространения с шестью нелинейными нейронами, так и двухслойной прямонаправленной искусственной нейронной сети. Перед использованием нейронной сети в режиме функционирования ее обучают решению конкретной задачи. Парадигмы обучения нейронных сетей разделяют на обучение с учителем и без него. Обучение с учителем предполагает, что для каждого входного вектора из обучающей выборки эксперт определяет целевой выходной вектор.
В нашем случае для решения задачи классификации степени активности автономной нервной системы была построена модель двухслойной прямонаправленной искусственной нейронной сети (61-10-6).
На вход сети поступают частоты ранжированной совокупности коррекций ритма сердца, сгруппированных по интервалам (-1,55; 1,5) ,..., (-0,1; -0,05), (-0,05; 0,05), (0,05; 0,1), ..., (1,5; 1,55).
Искусственная нейронная сеть обучена по алгоритму обратного распространения ошибки.
Алгоритм обучения включает следующие этапы:
1. Инициализация сети проводится со случайными значениями весовых коэффициентов.
2. Вычисление текущих выходных сигналов для случайно выбранного из обучающей выборки входного вектора.
3. Настройка синаптических весов.
Коррекции весовых коэффициентов связи осуществляются в направлении антиградиента целевой функции:
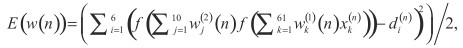
где n - дискретное время; w - матрица весовых коэффициентов связи; xk(n) - k-я координата входного вектора, поданного в момент времени n; di(n) - i-я координата соответствующего целевого вектора, сформированного врачом-экспертом; f(.) - биполярная сигмоидальная функция активации нейронов скрытого и выходного слоев.
4. Шаги 2‒3 повторяются для указанного временного диапазона.
При работе сети в режиме функционирования отклик сети на входной вектор определяется по формулам:
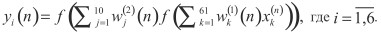 .
.
Распознавание класса производится по максимальному уровню выходного сигнала нейрона, связанного при обучении с одним из шести классов: РВП СНС, ВП СНС, УП СНС, Норма, УП ПСНС, ВП ПСНСП.
Для реализации рассмотренного алгоритма было разработано программное средство модульной структуры.
Модуль ввода электрофизиологической информации содержит датчик пульса на оптопаре.
Модуль обучения нейросети включает четыре блока. В блоке 1 находится матрица межпульсовых интервалов размера 82×500. На экране виден только ее фрагмент. Чтобы полностью увидеть данные, нужно воспользоваться полосами прокрутки или клавишами со стрелками.
Во втором блоке отображается фактический отклик сети на конкретную обучающую сессию. Каждому вектору межпульсовых интервалов соответствует вектор весовых коэффициентов. Максимальное значение отклика определяет класс, к которому сеть относит пример.
В третьем блоке для каждого примера из обучающей выборки (массива межпульсовых интервалов) определен целевой файл отклика нейросети. Значение 0,5 соответствует номеру класса, к которому отнес эксперт данный пример. Экспертом в данном случае выступает энтропийный алгоритм.
Четвертый блок содержит информацию о человеке, которому принадлежит межпульсовой интервал, а также вычисляется нормированная энтропия и выводится степень активности автономной нервной системы по алгоритму принятия решения через значение энтропии.
Пятый блок можно рассматривать как функциональный, поскольку в нем можно настраивать параметры, влияющие на результаты обучения сети: скорость и количество сеансов обучения. Значения, установленные по умолчанию, можно менять.
История ошибки сети отображается в шестом блоке. При повторном обучении сети средняя ошибка уменьшается.
В седьмом блоке в табличной форме отображаются текущие результаты обучения с примерами ошибочных решений. При выборе номера примера информация о нем появляется в четвертом блоке.
Ложноотрицательные результаты распознавания, или ошибки пропуска более тяжелого состояния (заболевания), относят к ошибкам первого рода (α) или числу случаев гиподиагностики.
Ложноположительные результаты распознавания, или отнесение здоровых людей к категории больных, относят к ошибкам 2-го рода (β) или числу случаев гипердиагностики.
В нашем исследовании, например, в блоке «гипердиагностика» экспертом указана «Норма», а нейросетевой алгоритм относит случай к «ВП СНС». Это, по сути, означает, что человек здоров, а врач ему ставит диагноз язвы желудка, то есть это типичная гипердиагностика.
К гипердиагностике относят и все те случаи, когда программа распознавания завысила класс, например, экспертная оценка вектора межпульсовых интервалов соответствует классу «УП СНС», а нейросетевой алгоритм относит данный вектор межпульсовых интервалов к классу «ВП СНС» или «РВП СНС». Также и внутри вагусной группы классов с преобладанием активности парасимпатической нервной системы. Например, экспертная оценка соответствует классу «УП ПСНС», а нейросетевой алгоритм относит этот вектор межпульсовых интервалов к «ВП ПСНС».
Что следует относить к случаям гиподиагностики? Например, эксперт выставил «УП СНС» или «УП ПСНС», а нейросетевой алгоритм относит это к «Норме». Или если нейросетевой алгоритм занизил класс, эксперт выставил «РВП СНС», а по нейросетевому алгоритму выходит «ВП СНС», «УП СНС», «Норма», «УП ПСНС», «ВП ПСНС» (как бы отнесение явно больного в группу здоровых лиц, или занижение степени тяжести заболевания).
При первом запуске процесса обучения сеть стартует со случайной точки. Поэтому результаты классификации при разных запусках программы могут отличаться.
Как правило, после 30 000 итераций (время обучения - 2 мин) сеть устойчиво выходит на 90 % верной классификации и ошибается только в граничных случаях. Последний факт можно увидеть, если посмотреть на значение нормированной энтропии для примеров с ошибками. Под эпохой анализа понимается предъявление сети по одному разу всех примеров из обучающей выборки.
В табл. 1 рассмотрены результаты эффективности распознавания степени активности АНС на примере обучающей выборки.
Таблица 1
Анализ эффективности нейросетевого алгорима классификации степени активности
автономной нервной системы на обучающей выборке
|
№ п/п |
Степень |
Общее |
Правильно |
Неправильно распознано |
||
|
Ист+ |
Ист‒ |
Гиподиагностика |
Гипердиагностика |
|||
|
1 |
УП СНС |
53 % |
40,5 % |
12 % |
0 % |
0,5 % |
|
2 |
ВП СНС |
4 % |
0,5 % |
2,0 % |
0 % |
1,5 % |
|
3 |
РВП СНС |
27 % |
19 % |
7,3 % |
0 % |
0,7 % |
|
4 |
Норма |
6 % |
4,0 % |
2,0 % |
0 % |
0 % |
|
5 |
УП ПСНС |
7 % |
5,0 % |
0,7 % |
0 % |
1,3 % |
|
6 |
ВП ПСНС |
3 % |
1,0 |
2,0 % |
0 % |
0 |
|
7 |
Итого: человек, % |
139‒100 % |
97‒70,0 % |
36‒26,0 % |
‒0,0 % |
6‒4,0 % |
Из представленных в табл. 1 данных следует, что нейросетевой алгоритм на обучающей выборке правильно отобрал 94,0 % больных. Неправильно распознано - 4,0 %. Из них гиподиагностика составила всего 4,0 %, случаев гипердиагностики алгоритм не допустил.
Чувствительность алгоритма распознавания составила 100,0 % (70,0/70,0 + 0,0), специфичность дифференциальной диагностики - 86,7 % (26,0/26,0 + 4,0).
В табл. 2 рассмотрены результаты эффективности распознавания степени активности АНС на примере экзаменационной выборки.
Таблица 2
Анализ эффективности нейросетевого алгорима классификации степени активности
автономной нервной системы на экзаменационной выборке
|
№ п/п |
Степень |
Общее |
Правильно |
Неправильно распознано |
||
|
Ист+ |
Ист‒ |
Гиподиагнос-тика |
Гипердиагностика |
|||
|
1 |
УП СНС |
6 % |
4,6 % |
1 % |
0,3 % |
0,1 % |
|
2 |
ВП СНС |
48 % |
32,4 % |
14 % |
0,2 % |
1,4 % |
|
3 |
РВП СНС |
20 % |
20 % |
0 % |
0 % |
0 % |
|
4 |
Норма |
2 % |
2,0 % |
0 % |
0 % |
0 % |
|
5 |
УП ПСНС |
16 % |
4,0 % |
7,0 % |
1,5 % |
3,5 % |
|
6 |
ВП ПСНС |
8 % |
5,0 |
3,0 % |
0 |
0 |
|
7 |
Итого: человек, % |
50‒100 % |
34‒68 % |
12‒25 % |
1‒2 % |
3‒5 % |
Из представленных в табл. 2 данных следует, что нейросетевой алгоритм на экзаменационной выборке правильно отобрал 93,0 % больных. Неправильно распознано - 7,0 %. Из них гипердиагностика составила 5,0 % и гиподиагностика 2,0 %.
Чувствительность алгоритма распознавания составила 97,1 % (68,0/68,0 + 2,0), специфичность дифференциальной диагностики - 83,3 % (25,0/25,0 + 5,0).
Выводы
1. Разработана модель двухслойной прямонаправленной искусственной нейронной сети, отличающаяся наличием обучающего алгоритма с использованием обратного распространения ошибки.
2. Проанализированы критерии оценки эффективности нейросетевого алгоритма распознавания степени активности АНС на обучающей и экзаменационной выборках.
3. Чувствительность нейросетевого алгоритма классификации степени активности АНС на экзаменационной выборке составляет 97,1 %, способность к дифференциальной диагностике - 83,3 %.
4. Ошибки классификации составили 7 %, что существенно ниже ошибок распознавания, допускаемых врачом. Нейросетевой алгоритм завысил класс степени активности АНС только в 5 % случаев, а занизил всего лишь в 2 % случаев.
Список литературы
- Макконен К.Ф. Игровой модуль с реализацией стратегии, направленной на избегание неудачи / К.Ф. Макконен, Ф.А. Пятакович, А.С. Новоченко // Фундаментальные исследования. - 2007. - №1. - С. 70-72.
- Макконен К.Ф. Модели и алгоритмы биоуправления в информационной системе игрового автомобильного тренинга / К.Ф. Макконен, Ф.А. Пятакович // Системный анализ и управление в биомедицинских системах: журнал практической и теоретической биологии и медицины. - М., 2008. -Т. 7, № 1. - С. 177-181.
- Пятакович Ф.А., Макконен К.Ф., Новоченко А.С. Патент №2349156. Биоуправляемый игровой тренажер и способ коррекции функционального состояния человека. Заявка №2007117796, приоритет 14 мая 2007 г. Зарегистрированный в государственном реестре Российской Федерации 20 марта 2009 г.
- Пятакович Ф.А., Якунченко Т.И. Способ диагностики успешности и эффективности биоуправляемого игрового тренинга по динамике отношения пульса и дыхания на основе использования обучающихся нейронных сетей //
International journal on immunorehabilitation. Международный журнал по иммунореабилитации. - 2010. - Т. 12, №2. - С. 226.
Рецензент ‒
Афанасьев Юрий Иванович, д.м.н., профессор, зав. кафедрой внутренних болезней №1, ГОУ ВПО «Белгородский государственный университет».



