В связи с бурным развитием инженерной деятельности, появлением конструкций и сооружений, работающих в условиях стационарного и нестационарного нагрева, появилась тенденция перехода от допустимых инженерных решений к оптимальным, возникла потребность в решении оптимизационных задач термоупругости и термопластичности.
Конструкции, одновременно работающие на силовые и температурные воздействия, широко применяются в различных отраслях народного хозяйства: будь то выплавка чугуна и стали, термообработка металла, изготовление и переработка нефтепродуктов и химических удобрений, сушка и обжиг строительных материалов и т.д.
Остановимся на изопериметрической задаче формообразования конструкции из однородного материала при заданном объеме V0. В этом случае функционал, соответствующий используемому вариационному принципу, содержит слагаемое, отражающее дополнительное условие, с множителем Лагранжа λ, который в изопериметрической задаче является постоянной величиной.
Обратимся к принципу возможных изменений напряженного состояния и рассмотрим проектную задачу для стержневой системы. Функционал Кастильяно имеет вид [1]:
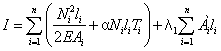, (1)
где Ni - продольное усилие в i-ом стержне, число которых n, от силового воздействия; li и Ai - длина и площадь поперечного сечения; E - модуль продольной упругости, α - коэффициент линейного расширения материала; Ti - температура i-го стержня.
Следствием стационарности функционала являются m уравнений совместности деформаций (m - число лишних связей):
(2)
уравнение объема
(3)
и r уравнений структурообразования ( r - число варьируемых параметров); в частности, при варьировании площадей сечений они принимают вид
(4)
В общем случае получаем систему нелинейных уравнений, которую можно решить с помощью ЭВМ. В определенных случаях систему можно свести к одному разрешающему уравнению, которое носит также нелинейный характер.
Уравнения структурообразования являются составляющими критерия рациональности конструкции фермы. Так, уравнения (4) свидетельствуют о равнонапряженности стержневой системы из однородного материала.
В то же время можно задать величину потенциальной энергии деформации системы I0 и определить конфигурацию из условия, чтобы функционал объема V достиг стационарного значения. В этом случае функционал свободной вариационной задачи имеет вид
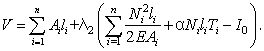(5)
В силу двойственности постановки вариационных задач на условный экстремум с интегральными связями имеем соотношение 
. Следовательно,
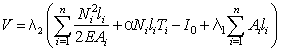, (6)
и мы, по существу, возвращаемся к предыдущей задаче. Исключение составляют случаи 
и 
, имеющие характер вырождения решения. Решения рассмотренных задач совпадают с точностью до постоянного множителя λ.
В стержневых системах со сжатыми стержнями необходимо выполнение условия безопасной устойчивости. Это эквивалентно введению виртуального состояния с внутренними силами 
для сжатых стержней ( 
- коэффициент уменьшения расчетного сопротивления R). При этом уравнение (4) остается справедливым для растянутых стержней, для сжатых стержней оно принимает вид
(7)
Расширим функциональное пространство за счет угла β, определяющего геометрию фермы. Следствием стационарности функционала (1), кроме прежних уравнений будет уравнение из условия
(8)
Задание величины V0 и I0 требует определенного опыта проектирования конструкции, в связи с чем решение задачи ведется методом последовательных приближений. При чисто силовом воздействии одинаково приемлемы обе постановки задачи - с функционалами (1) и (5). При наличии температурного воздействия выгоднее использовать функционал (6).