![]() , где
, где ![]() - непустое конечное множество позиций;
- непустое конечное множество позиций;![]() - непустое конечное множество переходов;
- непустое конечное множество переходов;
![]() - отношение инцидентности позиций и переходов; B - функция кратности дуг:
- отношение инцидентности позиций и переходов; B - функция кратности дуг: ![]() - функция нечеткого времени срабатывания переходов сети;
- функция нечеткого времени срабатывания переходов сети;![]() -функция нечеткого времени задержки;
-функция нечеткого времени задержки; ![]() - начальная маркировка сети;
- начальная маркировка сети; ![]() - множество натуральных чисел; g - множество нечетких чисел.
- множество натуральных чисел; g - множество нечетких чисел.
Множеством входных позиций перехода называется множество ![]() , а множеством выходных позиций соответственно
, а множеством выходных позиций соответственно ![]() .
.
Разберем алгоритм построения ленты достижимости, он условно разбивается на следующие фазы.
Исходные данные: НВСП
![]() .
.
Начальная установка:
![]() - нечеткое время работы сети, где i=0;
- нечеткое время работы сети, где i=0;
![]() - текущая маркировка, где i=0;
- текущая маркировка, где i=0;
M - множество текущих маркировок;
![]() - множество переходов, для которой выполнено условие активизации;
- множество переходов, для которой выполнено условие активизации;
![]() - h-ая ключевая последовательность, где h=1;
- h-ая ключевая последовательность, где h=1;
g - длина h-ой ключевой последовательности ![]() , где h=1, g=1;
, где h=1, g=1;
![]() - множество ключевых последовательностей
- множество ключевых последовательностей ![]() .
.
1.Формируем множество текущих маркировок M срабатывания переходов
1.1. Если М=Ø, тогда goto10.
1.2. Если М≠Ø, тогда goto2.
2.Выбираем маркировку
и удаляем из М.
3. Для маркировки
формируем множество переходов
, для которых выполняется условие активизации.
4. Проверка маркировок на тупики.
4.1. Если
=Ø, тогда
- маркировка тупиковая,
- удаляется из
со значением «тупик».
4.1.1. Если М≠Ø, тогда goto2.
4.1.2. Если М=Ø, тогда М:=М´, goto1.
4.2. Если
≠Ø, тогда
- маркировка не тупиковая, goto5.
5.Поиск возможных вариантов срабатывания переходов, где каждый вариант увеличивает
еще на одну ключевую последовательность, причем
.
6. Сработавшие переходы tj доступны в нечеткий момент времени
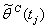
7. Вычисляются маркировки
8. Проверка маркировок на циклы.
8.1. Если
- циклическая маркировка, тогда
- удаляется из
со значением «цикл».
9. Не циклические маркировки присваиваются множеству маркировок М´.
9.1. Если М=Ø, тогда М:=М´, goto1.
9.2. Если М≠Ø, тогда goto2.
10. Конец алгоритма.
В данном случае алгоритм носит более сложный характер, чем в классических и временных модификациях сетей Петри. Этот алгоритм годится так же для построения дерева достижимости. Если нечеткие временные сети Петри мы преобразуем в матричный вид, тогда благодаря этому алгоритму можно будет провести матричный анализ.
СПИСОК ЛИТЕРАТУРЫ
- Котов В.Е. Сети Петри. - М.: Наука, 1984. - 160 с.
- Murata, M., "Temporal Uncertainty and Fuzzy-Timing High-Level Petri Nets," Invited paper at the 17th International Conference on Application and Theory of Petri Nets, Osaka, Japan, LNCS Vol. 1091, pp. 11-28. 1996.
- Юдицкий С. А. «Сценарный подход к моделированию поведения бизнес - систем». Серия «Управление организационными системами». - М.: СИНТЕГ, 2001, 112с.
Библиографическая ссылка
Ефимов М. И., Желтов В. П. АЛГОРИТМЫ АНАЛИЗА ДЛЯ НЕЧЕТКИХ ВРЕМЕННЫХ СЕТЕЙ ПЕТРИ // Фундаментальные исследования. 2004. № 6. С. 113-113;URL: https://fundamental-research.ru/ru/article/view?id=6498 (дата обращения: 20.12.2025).



