Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы

Иванов Е.М.

На основе баланса импульсов сил выводится уравнение баланса энергий (работ). Показано, что это уравнение есть I закон термодинамики применительно к механическим процессам.

Статья в формате PDF

120 KB

Если на тело массы m в течение времени t действует сила F(t), то импульс силы определится интегралом

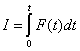                                 (1)

II закон Ньютона определяется выражением . В дальнейшем ограничимся рассмотрением постоянных сил. Тогда , где  - импульс тела (количество движения).

Работу определим как производство энергии импульсом силы

                                    (2)

где E - произведенная энергия. В частности, если тело находится на гладкой горизонтальной поверхности и на него действует горизонтальная сила F, то ускорение ,  и формула (2) преобразуется к общеизвестной формуле , которая является частным случаем более общей формулы (2), а произведенная энергия равна .

Рассмотрим случай движения тела по шероховатой горизонтальной поверхности под действием силы F, действующей под углом α к горизонту (рис 1).

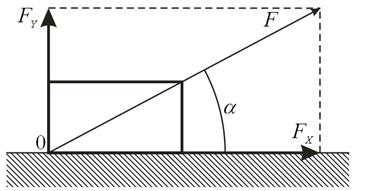
Рисунок 1. Движения тела по шероховатой горизонтальной поверхности под действием силы , действующей под углом  к горизонту

Силу F раскладываем на две составляющие:  и . Силу  назовем силой левитации , она уменьшает силу давления тела на плоскость, а при величине  тело оказывается в квазиневесомом состоянии (состояние левитации). Сила  вызывает деформацию тела (сжатия, растяжения, изгиба) в зависимости от способа приложения силы F. Сила  совершает работу левитации:

              (3)

Работу, которую совершает сила , определяется аналогично:

                                               (4)

Поскольку силы F_X и F_Л взаимноперпендикулярны, то в соответствии с теоремой Пифагора  и поэтому работы этих сил аддитивны, т.е.

               (5)

Сила может быть представлена в виде суммы трех сил: , где F_a - результирующая сила в горизонтальном направлении, входящая во II закон Ньютона и вызывающая ускоренное движение тела вдоль оси Х: . На преодоление трения затрачивается сила . На деформацию тела в продольном направлении затрачивается сила . Вот как об этом пишется в учебнике Г.С. Ландсберга [1, с.142]: «...ускоряемое тело может начать двигаться как целое только после того, как внутри него возникнут деформации, а вместе с ними и силы упругости, которые сообщат внутренним частям тела требуемое ускорение». Квадрат импульса силы  запишется в виде

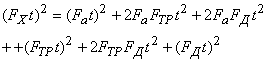    (6)

Это баланс импульсов сил, действующих вдоль оси Х. Разделив обе части равенства на 2m, получим баланс энергий (работ), затрачиваемых на движение вдоль оси Х:

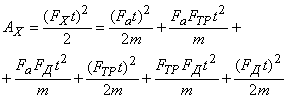 (7)

Выражение (7) показывает, что работа сил, действующих вдоль одной оси, не аддитивна, т.е. не является простой арифметической суммой работ этих сил. Первый член правой части  - работа, затраченная на разгон тела (получение кинетической энергии). Все работы в правой части (7) связанные с силой трения , еще в процессе движения переходят во внутреннюю энергию (нагрев трущихся поверхностей):

    (8)

Все работы, связанные с деформацией, в том числе и работа левитации (3), после снятия нагрузки F тоже переходят во внутреннюю энергию, т.к. после снятия нагрузки в теле возникают упругие колебания, которые вследствие дисперсии и внутреннего трения быстро переходят во внутреннюю энергию (тело разогревается). Работу этих сил можно назвать латентной (скрытой) внутренней энергией:

      (9)

Таким образом, баланс энергий (работ) можно записать в следующем виде:

                            (10)

где  - энергия, подводимая извне за счет действия импульса силы. Выражение (10) есть не что иное, как первый закон термодинамики в применении к механическим процессам.

СПИСОК ЛИТЕРАТУРЫ

1. Элементарный учебник физики. Под редакцией академика Г.С. Ландсберга. М.: Наука, 1972. Том 1.

Библиографическая ссылка