Работа перемещения заряда вдоль линии напряженности электростатического поля Aφ = q (φ1 - φ2 ). При перемещении заряда в обратном направлении работа сторонних сил имеет минимум, величина которого зависит от способа приложения сторонней силы.
Рассмотрим движение положительного заряда q в однородном электрическом поле напряженности E плоского конденсатора (рис.1а) в отсутствии сил гравитационного поля.
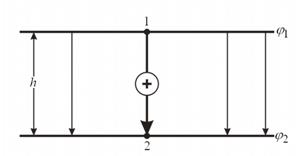
Рисунок 1 (а). Движение положительного заряда q в однородном электрическом поле напряженности E плоского конденсатора.
Под действием кулоновской силы ![]() движение заряда из точки 1 потенциальной плоскости
движение заряда из точки 1 потенциальной плоскости ![]() в точку 2 потенциальной плоскости
в точку 2 потенциальной плоскости ![]() может происходить только вдоль линии напряженности поля (в данном случае вертикальная линия 1-2). Расстояние между плоскостями
может происходить только вдоль линии напряженности поля (в данном случае вертикальная линия 1-2). Расстояние между плоскостями ![]() . На основании II закона Ньютона:
. На основании II закона Ньютона:
![]() ;
; ![]() ,
,
где t - время движения заряда. Работу перемещения заряда представим в двух видах:
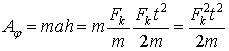 (1)
(1)
![]() (2)
(2)
Отметим, что для того, чтобы остановить заряд в точке 2, необходимо затратить работу торможения, равную![]() .
.
Чтобы вернуть заряд q по тому же пути из точки 2 в точку 1, необходимо приложить стороннюю силу F (рис.1б), которую можно представить в виде суммы ![]() , где
, где ![]() - сила, равная по модулю кулоновской силе
- сила, равная по модулю кулоновской силе ![]() , обеспечивающая равновесие заряда (неподвижность) в электростатическом поле, которую назовем силой левитации.
, обеспечивающая равновесие заряда (неподвижность) в электростатическом поле, которую назовем силой левитации.
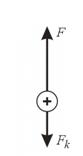
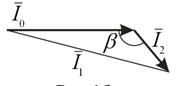
Рисунок 1 (б)
Если ![]() , то перемещение заряда вверх не происходит, поскольку
, то перемещение заряда вверх не происходит, поскольку ![]() . Если
. Если ![]() , то начинает работать II закон Ньютона: ускорение
, то начинает работать II закон Ньютона: ускорение ![]() ;
; ![]() . Время движения вверх
. Время движения вверх
![]() (3)
(3)
Запишем баланс импульсов сил:
![]() (4)
(4)
Возведя в квадрат и разделив на 2m обе части равенства, получим баланс энергий (работ):
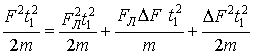 (5)
(5)
Или
![]() (5а)
(5а)
где ![]() - работа силы левитации в статическом состоянии,
- работа силы левитации в статическом состоянии, ![]() - обычная работа силы
- обычная работа силы ![]() , вызывающей ускоренное движение,
, вызывающей ускоренное движение, ![]() - работа, связанная с ускоренным движением силы левитации,
- работа, связанная с ускоренным движением силы левитации, ![]() - суммарная работа сторонней силы F.
- суммарная работа сторонней силы F.
Выразим эти работы через работу ![]() , определяемую выражением (2).
, определяемую выражением (2).
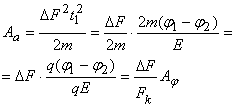 (6)
(6)
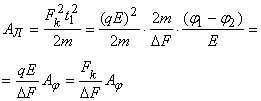 (7)
(7)
![]() (8)
(8)
Таким образом, зависимость между работами ![]() и
и ![]() имеет гиперболический характер.
имеет гиперболический характер.
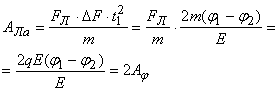 (9)
(9)
Тогда суммарную работу сторонней силы F можно записать так
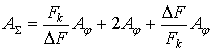 (10)
(10)
Это выражение имеет минимум в случае ![]() , равный
, равный ![]() . На графике (рис.2) показана зависимость суммарной работы
. На графике (рис.2) показана зависимость суммарной работы ![]() от соотношения
от соотношения ![]() .
.
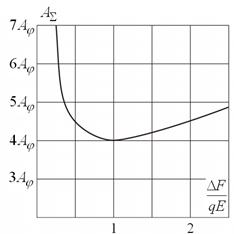
Рисунок 2. Зависимость суммарной работы ![]() от соотношения
от соотношения ![]()
Из графика видно, что даже в самом благоприятном случае работа подъема заряда сторонней силой в 4 раза больше работы кулоновской силы, совершающей перемещение заряда вниз. Здесь необходимо отметить следующее: кулоновская сила препятствует перемещению заряда вверх, т.е. совершает отрицательную работу, но по модулю она не равна ![]() , поскольку движение происходит под действием силы ΔF в течение времени t1, которое связано с временем t формулы (1) соотношением:
, поскольку движение происходит под действием силы ΔF в течение времени t1, которое связано с временем t формулы (1) соотношением: ![]() . Тогда работа кулоновской силы будет равна
. Тогда работа кулоновской силы будет равна
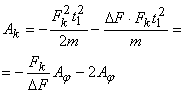 (11)
(11)
Рассмотрим другой вариант перемещения заряда из точки 2 в точку 1 за счет действия мгновенной силы [1,2,3] в виде ![]() , где
, где ![]() -
- ![]() -функция Дирака. Величину
-функция Дирака. Величину ![]() будем называть единичным импульсом силы. Тогда дифференциальное уравнение движения заряда запишется в виде:
будем называть единичным импульсом силы. Тогда дифференциальное уравнение движения заряда запишется в виде:
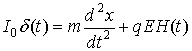 (12)
(12)
при нулевых начальных условиях: ![]() и
и ![]() . H(t) - единичная (ступенчатая) функция Хевисайда, причем
. H(t) - единичная (ступенчатая) функция Хевисайда, причем ![]() [1,4]. Для решения задачи используем преобразование Лапласа [4]. Получаем:
[1,4]. Для решения задачи используем преобразование Лапласа [4]. Получаем:
![]() ;
; ![]() (13)
(13)
Определим работу, совершаемую при перемещении заряда из точки 1 в точку 2:
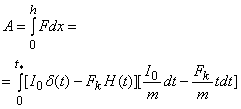 (14)
(14)
Вычисляя интегралы, получим
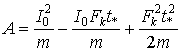 ;
;
![]() (15)
(15)
Под действием мгновенного импульса силы заряд приобретает скорость ![]() , направленную вверх, а под действием кулоновской силы возникает тормозящее ускорение:
, направленную вверх, а под действием кулоновской силы возникает тормозящее ускорение: ![]() . Время движения заряда
. Время движения заряда ![]() или
или ![]() . Оно равно времени t формулы (1).
. Оно равно времени t формулы (1).
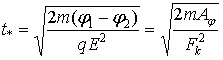 (16)
(16)
Энергия, приобретенная зарядом от единичного импульса силы ![]() , а остальные члены уравнения (15) можно представить в виде:
, а остальные члены уравнения (15) можно представить в виде:
![]() ;
;
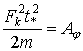
Последний член представляет собой повышение потенциальной энергии при перемещении заряда из точки 2 в точку 1. Таким образом, при движении заряда за счет действия мгновенной силы, заряд должен получить извне начальную энергию A0, равную ![]() .
.
Рассмотрим третий вариант перемещения заряда из 2 в 1. На заряд действует сторонняя сила, равная кулоновской, но направленная в противоположную сторону (сила левитации): ![]() , а для перемещения заряда вверх ему сообщается единичный импульс силы
, а для перемещения заряда вверх ему сообщается единичный импульс силы ![]() за счет действия мгновенной силы
за счет действия мгновенной силы ![]() . Дифференциальное уравнение движения примет вид:
. Дифференциальное уравнение движения примет вид:
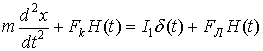 (17)
(17)
при нулевых начальных условиях. Решая уравнение с помощью преобразования Лапласа и вычисляя работу, получим:
Положительная работа:
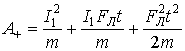 (18)
(18)
Отрицательная работа (противодействующая перемещению заряда):
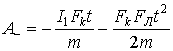 (19)
(19)
Время движения заряда ![]() . В окончательном виде положительная работа (при
. В окончательном виде положительная работа (при ![]() ):
):
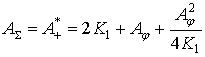 ;
;
![]() (20)
(20)
Это выражение имеет минимум, равный ![]() при значении
при значении ![]() . На графике (рис.3) показана зависимость суммарной положительной работы
. На графике (рис.3) показана зависимость суммарной положительной работы ![]() , выраженной в долях работы Aφ, от величины отношения
, выраженной в долях работы Aφ, от величины отношения ![]() .
.
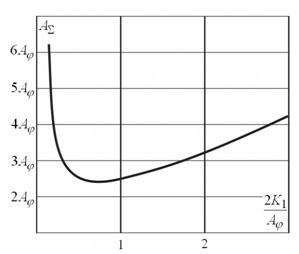
Рисунок 3. Зависимость суммарной положительной работы ![]() , выраженной в долях работыAφ , от величины отношения
, выраженной в долях работыAφ , от величины отношения ![]() .
.
Отрицательная работа в окончательном виде (при ![]() ):
):
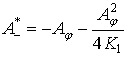 (21)
(21)
Как следует из графика (рис.4) отрицательная работа (работа кулоновской силы) не является постоянной величиной. Ее можно вычислять по формуле (2) только в том случае, если она является единственной движущей (или тормозящей) силой. Когда же кулоновская сила «соучаствует» со сторонними силами в перемещении заряда, то изменяется время движения заряда и расчет работы кулоновской силы надо проводить с учетом ее взаимодействия с другими силами. При очень большом начальном импульсе (![]() ) выражение (21) асимптотически стремится к обычному значению работы кулоновской силы:
) выражение (21) асимптотически стремится к обычному значению работы кулоновской силы: ![]() .
.
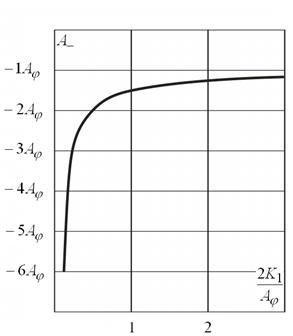
Рисунок 4. Работа кулоновской силы
СПИСОК ЛИТЕРАТУРЫ
- Арфкен Г. Математические методы в физике. - М.: Атомиздат, 1970.
- Иванов Е.М. Дополнительные главы классической механики. - Димитровград: ДИТУД УлГТУ, 2004.
- Иванов Е.М. Работа центростремительных и гироскопических сил //Успехи современного естествознания - №9. - 2004.
- Дёч Г. Руководство к практическому применению преобразования Лапласа. М.: Наука, 1971.
Библиографическая ссылка
Иванов Е.М. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ // Фундаментальные исследования. 2005. № 7. С. 9-13;URL: https://fundamental-research.ru/ru/article/view?id=6319 (дата обращения: 11.02.2026).



