При статистическом исследовании финансово-экономических показателей в ходе анализа вычисляют простейшие характеристики, выявляют закономерности прошлого развития и оценивают возможность их перенесения на будущее. Является актуальной задача прогнозирования и планирования структуры и объема долга субъекта Российской Федерации. Процентные ставки имеют большое значение в моделях управления государственным долгом. Но чаще всего они нелинейно входят в бюджетное ограничение и неоднозначно влияют на выбор оптимальной структуры государственного долга [1].
Актуальной является задача выбора вида заимствований. При этом необходимо распределить ресурсы между альтернативами (затраты на оформление заимствований). В частности, интерес представляют задачи комбинаторной оптимизации, самая простая из которых - определение комбинации (альтернатив, проектов заимствований), максимизирующей "общие выгоды" при ограничениях на издержки. Общая постановка задачи определения комбинации альтернатив с максимальной эффективностью (или эффективностью на единицу требуемого ресурса) заключается в определении сочетаний альтернатив [2], удовлетворяющих следующим целевым функциям:
![]() , (1)
, (1)
![]() , (2)
, (2)
при выполнении одного из следующих условий:
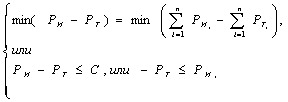 (3)
(3)
где
Э - эффективность рассматриваемой комбинации альтернатив, полученной генерацией множества сочетаний с различным числом альтернатив;
Эi- эффективность i-й альтернативы, входящей в рассматриваемую комбинацию из n альтернатив;
Рт - требуемый ресурс рассматриваемой комбинации альтернатив;
Ртi- требуемый ресурс i-й альтернативы, входящей в рассматриваемую комбинацию из n альтернатив;
РИ- имеющийся в наличии ресурс рассматриваемой комбинации альтернатив;
РИi - имеющийся в наличии ресурс i-й альтернативы, входящей в рассматриваемую комбинацию из n альтернатив;
С - заданное пороговое значение ресурса.
В качестве ресурса можно рассматривать как денежные средства, так и интервалы времени. Эффективность каждой альтернативы рассчитывается как отношение разности приведенной стоимости обязательства и затрат на обслуживание к самой приведенной стоимости обязательства: Э = (PV-З)/PV.
Эффективность исходного множества альтернатив рассчитывается на основе множества критериев и может быть определена либо на одной иерархии, отражающей критерии эффективности, либо на основе отражения значений векторов приоритетов альтернатив, характеризующих выгоды и издержки, получаемые от их реализации.
Существуют ситуации, в которых при распределении ресурсов руководствуются следующим правилом: делать как можно больше при ограниченных (имеющихся в наличии) ресурсах. Целевая функция в данной задаче имеет вид:
![]()
при выполнении одного из условий
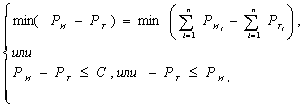
где
Na - число возможных сочетаний альтернатив;
Аi - альтернатива, на которую распределяется ресурс.
Таким образом, для решения задачи комбинаторной оптимизации необходимо, прежде всего, сгенерировать множество всех возможных сочетаний (комбинаций) из n-го числа альтернатив. В указанное множество должны входить парные сочетания, тернарные сочетания и далее все n - 1 сочетания, а также сочетание, состоящее из всех п альтернатив. Максимальное число возможных сочетаний NK для данной задачи определяется на основе следующей формулы:
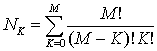 ,
,
где
К - число альтернатив в i-й комбинации, принимающее значение в диапазоне [0,М];
М - максимальное число рассматриваемых альтернатив.
Определим множество комбинаций с различными числом и составом альтернатив.
Допустим, имеется множество из М альтернатив и каждой альтернативе соответствует ее уникальный порядковый номер.
Требуется из заданного множества получить комбинации всех возможных альтернатив, которые должны удовлетворять следующим условиям [6]: 1) в каждой i-й комбинации не должно присутствовать одинаковых альтернатив; 2) каждая i-я комбинация должна отличаться от других не менее чем одной альтернативой; 3) комбинации альтернатив должны содержать в общем случае все единичные, парные, тернарные и другие М-1 и М сочетания альтернатив. Каждой альтернативе в процессе генерации комбинаций присваиваются два типа признаков: "истина" (И) и "ложь" (Л).
В начальном состоянии всем альтернативам присваивается признак "ложь". В этом случае сгенерированная комбинация содержит нуль альтернатив. Далее осуществляется циклическое изменение признаков альтернатив и генерация из них новых комбинаций по следующим правилам.
Правило 1. Если альтернатива А1 множества А имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков у альтернатив. В противном случае, если альтернатива A1 множества A имеет признак "И", осуществляем переход к альтернативе А2.
Правило 2. Если i-я альтернатива Аi множества А имеет признак "Л", то изменяем его на признак "И" и заканчиваем изменение признаков альтернатив. В противном случае изменяем признак i-й альтернативы Аi множества А на "Л" и осуществляем переход к i+1 альтернативе Ai+1
Правило 3. Если альтернатива AN множества А имеет признак "Л", то изменяем его на "И" и заканчиваем изменение признаков альтернатив. В противном случае, если альтернатива AN имеет значение признака "И", то генерируемая на данной итерации комбинация является последней и содержит все альтернативы множества А.
Таким образом, генерируемая на каждой итерации комбинация включает альтернативы множества А, имеющие на текущей итерации значение признака "Истина".
В табл. 1 приведен пример генерации комбинаций с учетом приведенного выше алгоритма для множества А, включающего три альтернативы.
Таблица 1. Алгоритм генерации альтернатив
|
Номер итерации |
Состояние множества альтернатив Аi |
Альтернативы, определяющие генерируемую комбинацию |
||
|
1 |
А1 "Л" |
А2 "Л" |
А3 "Л" |
- |
|
2 |
А1* "И" |
А2 "Л" |
А3 "Л" |
А1 |
|
3 |
А1 "Л" |
А2* "И" |
А3 "Л" |
А2 |
|
4 |
А1 * "И" |
А2 "И" |
А3 "Л" |
А1 А2 |
|
5 |
А1 "Л" |
А2 "Л" |
А3 * "И" |
А3 |
|
6 |
А1* "И" |
А2 "Л" |
А3 "И" |
А1 А3 |
|
7 |
А1 "Л" |
А2* "И" |
Аз "И" |
А2 А3 |
|
8 |
А1* "И" |
А2 "И" |
А3 "И" |
А1 А2 А3 |
* отмечен последний изменившийся на итерации признак.
Алгоритм определения комбинации альтернатив, обеспечивающей оптимальное распределение ресурса, имеет следующий вид.
Шаг 1. Определяется М альтернатив, для каждой из которых устанавливается требуемый ресурс и вычисляется относительная эффективность.
Шаг 2. Генерируются все парные, тернарные, М-1 комбинации альтернатив.
Шаг 3. Для каждой сгенерированной комбинации определяются суммарные значения: требуемого ресурса, относительной эффективности и относительной эффективности на единицу требуемого ресурса.
Шаг 4. Определяется искомая комбинация альтернатив с учетом задаваемой целевой функции.
Рассмотрим пример распределения ресурса на комбинации альтернатив, представляющих программы заимствований: кредит, договор, выпуск облигаций, гарантия.
Относительная эффективность (полезность) программ заимствования оценена по комплексу иерархически упорядоченных критериев качества с трех точек зрения: экономиста-программиста, рассчитывающего различные проекты; бухгалтера, ведущего бухгалтерский анализ департамента финансов; руководителя, использующего результаты бухгалтерского анализа для принятия решений.
Методом анализа иерархий определен вектор приоритетов альтернатив, характеризующий их относительную эффективность. Относительная эффективность программ и требуемые для их оформления ресурсы (в условных денежных единицах) приведены в табл. 2.
Таблица 2. Исходные данные по эффективности и требуемому ресурсу
|
Параметр |
Альтернатива Аi |
|||
|
А1, |
А2 |
А3 |
А4 |
|
|
Относительная эффективность |
0,30 |
0,15 |
0,35 |
0,25 |
|
Требуемый ресурс |
10 |
5 |
5 |
3 |
Все возможные комбинации, состоящие из двух, трех и четырех альтернатив, суммарная эффективность комбинаций, требуемый на каждую операцию ресурс и эффективность на единицу ресурса приведены в табл. 3.
Таблица 3. Результаты распределения ресурса
|
Параметр |
Комбинация альтернатив |
||||||
|
А1 А2 |
А1 А3 |
А1 А4 |
А1 А2 А3 |
А1 А3 А4 |
А2 А3 А4 |
А1 А2 А3 А4 |
|
|
Суммарная эффективность комбинации |
0,45 |
0,65 |
0,50 |
0,80 |
0,85 |
0,80 |
1,0 |
|
Требуемый ресурс на комбинацию |
15 |
15 |
13 |
20 |
18 |
13 |
23 |
|
Эффективность на единицу ресурса |
0,03 |
0,043 |
0,031 |
0,040 |
0,047 |
0,061 |
0,043 |
Требуется определить такие комбинации альтернатив, на которые наиболее целесообразно распределить имеющийся ресурс (15 единиц ресурса) с учетом целевых функций (2) и (3) при условии min (Ри - Рт).
Искомыми комбинациями альтернатив для первой целевой функции является А2 А3А4, а для второй - А1 А2.
СПИСОК ЛИТЕРАТУРЫ
- Ковалишин Е.А., Поманский А.Б. Влияние неопределенности на структуру государственного долга./Экономика м математические методы, 2002, том 38, №4, с.60-69.
- Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике.- М.: Финансы и статистика, 2000.- 638 с.
Библиографическая ссылка
Чернышева Т.Ю. МОДЕЛЬ ДОЛГА С ФУНКЦИЕЙ МАКСИМУМА НА ЭФФЕКТИВНОСТЬ ЗАИМСТВОВАНИЙ // Фундаментальные исследования. 2006. № 4. С. 99-101;URL: https://fundamental-research.ru/ru/article/view?id=4999 (дата обращения: 28.02.2026).



