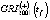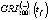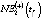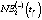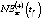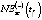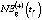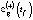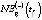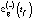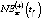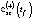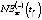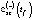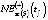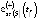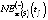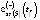Среднегодовая численность занятых в региональной экономике (NE) является одним из ключевых показателей, используемых при формировании прогнозов развития региональной социально-экономической системы (РСЭС) с различным горизонтом прогнозирования. В настоящее время для оценки динамики значений NE используются следующие методы:
- балансовые методы, на основе которых разрабатываются динамические балансовые модели трудовых ресурсов (балансы труда) экономических систем различной сложности [1–3];
- эконометрические методы, позволяющие разрабатывать комплексные модели динамики NE, оперирующие макроэкономическими показателями, характеризующими функционирование РСЭС [4–6];
- методы системной динамики [7–9].
Применение вышеперечисленных методов при разработке моделей оценки изменения значений NE и их краткосрочного прогнозирования сопряжено с определенными сложностями. Так, использование балансовых методов, несмотря на то, что методика построения баланса трудовых ресурсов разработана достаточно давно и успешно апробирована, в определенной степени затруднено, поскольку в открытой печати практически отсутствуют детализированные таблицы «Выпуск – Затраты» в региональном разрезе. Модели системной динамики не в полной мере специфицированы за исключением ряда в том числе и указанных работ с учетом структуры региональных показателей социально-экономического состояния субъектов федерации, публикуемых Росстатом РФ. Наиболее приемлемым вариантом для формирования краткосрочного прогноза значений NE, по мнению автора, являются эконометрические методы и модели, достаточно широко использующиеся и при «сценарном подходе» описания вариантов развития РСЭС, который в настоящее время активно используется профильными федеральными и региональными министерствами и департаментами.
Целью данной работы является формирование краткосрочного прогноза среднегодовой численности занятых в региональной экономике ХМАО-Югры на основе модификации использующегося в настоящее время комплекса эконометрических моделей, оперирующих ключевыми макроэкономическими показателями, характеризующими функционирование региональной социально-экономической системы в целом.
Материалы и методы исследования
Исходный комплекс моделей [4–6] включает следующие эконометрические модели:
– модель зависимости NE1(t) от численности трудоспособного населения региона WPR(t) вида
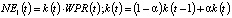 , (1)
, (1)
где α – постоянная, определяемая методами математической статистики на основе ретроспективных данных о WPR(t) и NE(t);
– модель определения NE2(t) в зависимости от оценки валового регионального продукта GRP(-)(t) для инерционного (базового, консервативного) и умеренно-оптимистического GRP(+)(t) (целевого) сценариев развития региональной экономики – 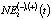 :
:
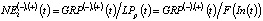 , (2)
, (2)
где LPр(t), In(t) – производительность труда и инвестиции в основной капитал региональной экономики; 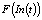 – зависимость, связывающая LPр(t) и In(t):
– зависимость, связывающая LPр(t) и In(t):
– 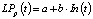 [4, 5]; (3)
[4, 5]; (3)
– 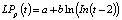 [6]; (4)
[6]; (4)
Здесь a, b – постоянные, определяемые методами математической статистики.
Непосредственно оценка 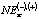 для каждого из сценариев развития региональной экономики осуществляется либо с использованием простой средней арифметической [4, 5]:
для каждого из сценариев развития региональной экономики осуществляется либо с использованием простой средней арифметической [4, 5]:
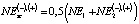 , (5)
, (5)
либо более сложной зависимостью [6]:
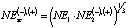 . (6)
. (6)
Зависимость (5), как правило, не требует дополнительного обоснования, так как предполагает равнозначность «влияния» на значения 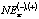 , как регионального демографического фактора в виде WPR(t), так и возможных сценариев развития региональной экономики, учитываемых через взаимосвязь LP(t) и In(t) (3), (4). Использование же выражения (6) в работе [6] недостаточно обосновано, что вызывает определенные сомнения в целесообразности его использования. В недостаточной мере, по мнению автора, обосновано использование и зависимостей (3), (4).
, как регионального демографического фактора в виде WPR(t), так и возможных сценариев развития региональной экономики, учитываемых через взаимосвязь LP(t) и In(t) (3), (4). Использование же выражения (6) в работе [6] недостаточно обосновано, что вызывает определенные сомнения в целесообразности его использования. В недостаточной мере, по мнению автора, обосновано использование и зависимостей (3), (4).
Модификацию комплекса эконометрических моделей (1)–(6) предлагается осуществить за счёт интеграции в исходный вариант эконометрической модели временного ряда NE(t) – NE3(t) и заменой 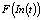 (3), (4) эконометрической моделью временного ряда LP(t). Оценку же
(3), (4) эконометрической моделью временного ряда LP(t). Оценку же 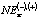 предлагается осуществлять с использованием простой средней арифметической.
предлагается осуществлять с использованием простой средней арифметической.
Непосредственно краткосрочное прогнозирование значения NEf(t) осуществляется по следующему алгоритму. Для временного интервала [t0, tk] предшествующему году прогнозирования tf строятся модели для оценки NE1(t) (2), 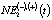 и NE3(t). Величина
и NE3(t). Величина 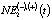 рассчитывалась согласно (2). Эконометрическая модель, характеризующая изменения производительности труда LPр(t) в рассматриваемой экономической системе, имеет следующий вид [10, 11]:
рассчитывалась согласно (2). Эконометрическая модель, характеризующая изменения производительности труда LPр(t) в рассматриваемой экономической системе, имеет следующий вид [10, 11]:
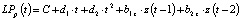 . (7)
. (7)
Здесь С, d1, d2 – постоянные, идентифицируемые при построении квадратичного тренда для значений LP(t) временного интервала [t0, tk]; z(t) – остатки, определяемые выражением
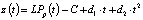 ; (8)
; (8)
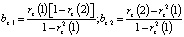 , (9)
, (9)
где rz(1), rz(2) – частные коэффициенты корреляции остатков (9).
Для описания изменений NE3(t) используется следующая зависимость [10, 11]:
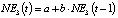 , (10)
, (10)
где a, b – постоянные, идентифицируемые методами математической статистики.
Исходя из допущения, что в году tf условия и характер функционирования рассматриваемой региональной экономики меняются незначительно, построенные модели используются для оценки величин NE1(tf), 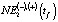 и NE3(tf). На их основании рассчитываются значения
и NE3(tf). На их основании рассчитываются значения 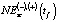 :
:
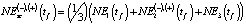 . (11)
. (11)
Далее алгоритм повторяется для следующего временного интервала. Для построения моделей динамики величин NE1(tf), 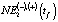 и NE3(tf) используются статистические данные о социально-экономическом состоянии ХМАО-Югры [12–14]. Оценка корректности идентифицируемых эконометрических моделей NE1(tf), LP(t) и NE3(tf) осуществлялась с использованием общепринятых статистических критериев R2, критерия Фишера, критерия Дарбина – Уотсона [10, 11]. Точность краткосрочного прогноза значения
и NE3(tf) используются статистические данные о социально-экономическом состоянии ХМАО-Югры [12–14]. Оценка корректности идентифицируемых эконометрических моделей NE1(tf), LP(t) и NE3(tf) осуществлялась с использованием общепринятых статистических критериев R2, критерия Фишера, критерия Дарбина – Уотсона [10, 11]. Точность краткосрочного прогноза значения 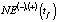 по отношению к фактическим значениям среднесписочной численности занятых в региональной экономике ХМАО-Югры
по отношению к фактическим значениям среднесписочной численности занятых в региональной экономике ХМАО-Югры 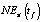 определялась выражением
определялась выражением
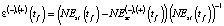 . (12)
. (12)
Наряду с этим значения 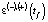 сопоставлялись с аналогичными значениями, рассчитанными для величин
сопоставлялись с аналогичными значениями, рассчитанными для величин 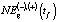 , которые публикуются профильным департаментом администрации округа в открытых источниках информации (https://gov.admhmao.ru/plany/prognoz-sotsialno-ekonomicheskogo-razvitiya-khmao-yugry/).
, которые публикуются профильным департаментом администрации округа в открытых источниках информации (https://gov.admhmao.ru/plany/prognoz-sotsialno-ekonomicheskogo-razvitiya-khmao-yugry/).
Результаты исследования и их обсуждение
Исходные данные, которые использовались при построении моделей NE1(tf), 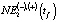 , NE3(tf),
, NE3(tf), 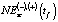 приведены в табл. 1 [12–14]. Величина валового продукта GRP2001(t) приведена в сопоставимых ценах 2001 г., а GRP(t) – в ценах соответствующего текущего года t.
приведены в табл. 1 [12–14]. Величина валового продукта GRP2001(t) приведена в сопоставимых ценах 2001 г., а GRP(t) – в ценах соответствующего текущего года t.
В табл. 2, 3, 4 приведены идентифицированные постоянные выражений (1), (7), (10). Расчетные значения статистических критериев, характеризующих точность R2, адекватность Fрасч отсутствие автокорреляции остатков – критерий Дарбина – Уотсона (KDW) построенных моделей, приведены в табл. 5. Для критерия KDW приведено значение [10, 11] его верхней границы d2(n, m), (n – количество наблюдений, m – количество степеней свободы (коэффициентов статистической модели)). Если расчетное значение KDW больше табличного d2(n, m), то это означает отсутствие автокорреляция между остатками.
Таблица 1
Макроэкономические показатели, характеризующие функционирование региональной экономики ХМАО-Югры в 2001–2018 гг.
|
Год |
NEst(t), тыс. чел. |
WPR(t), тыс. чел. |
GRP(t), млн руб. |
GRP2001(t), млн руб. |
LPр(t), (тыс. руб/чел.) |
|
2001 |
868,70 |
785 |
555 320,70 |
555 320,70 |
639,25 |
|
2002 |
878,00 |
793 |
589 378,90 |
569 203,72 |
648,30 |
|
2003 |
879,80 |
834 |
760 866,15 |
621 570,46 |
706,49 |
|
2004 |
873,50 |
827 |
1 026 962,53 |
670 674,53 |
767,80 |
|
2005 |
877,10 |
850 |
1 363 730,64 |
753 838,17 |
859,47 |
|
2006 |
879,40 |
848 |
1 666 318,90 |
804 345,32 |
914,65 |
|
2007 |
880,60 |
880 |
1 717 291,60 |
830 084,37 |
942,63 |
|
2008 |
890,40 |
906 |
1 937 159,10 |
854 156,82 |
959,30 |
|
2009 |
897,40 |
906 |
1 811 590,90 |
813 157,29 |
906,13 |
|
2010 |
897,60 |
916,00 |
1 971 870,50 |
837 552,01 |
933,10 |
|
2011 |
903,60 |
904,00 |
2 440 432,60 |
845 089,98 |
935,25 |
|
2012 |
912,20 |
913,00 |
2 703 558,80 |
829 033,27 |
908,83 |
|
2013 |
916,10 |
899,00 |
2 729 122,40 |
829 033,27 |
904,96 |
|
2014 |
917,20 |
916,00 |
2 860 498,90 |
818 255,84 |
892,12 |
|
2015 |
1037,40 |
918,00 |
3 154 058,70 |
803 527,23 |
774,56 |
|
2016 |
1025,40 |
918,00 |
3 068 148,50 |
784 242,58 |
764,82 |
|
2017 |
1077,90 |
917,00 |
3 511 127,50 |
784 242,58 |
727,57 |
|
2018 |
1085,70 |
917,00 |
3 967 100,00 |
786 595,31 |
724,51 |
Таблица 2
Идентифицированные значения коэффициента модели (1) NE1(t) для выделенных временных интервалов
|
Временной интервал |
2001–2012 гг. |
2001–2013 гг. |
2001–2014 гг. |
2001–2015 гг. |
2001–2016 гг. |
2001–2017 гг. |
|
α |
0,8 |
0,9 |
0,8 |
0,8 |
0,9 |
0,9 |
Таблица 3
Идентифицированные значения коэффициентов модели (7) LPр(t) и NE3(t) для выделенных временных интервалов
|
Временной интервал |
С |
d1 |
d2 |
bz.1 |
bz.2 |
|
Модель LPр(t) |
|||||
|
2001–2012 гг. |
507,88 |
92,901 |
-4,9533 |
0,293 |
-0,3963 |
|
2001–2013 гг. |
513,99 |
89,701 |
-4,6624 |
0,319 |
-0,3475 |
|
2001–2014 гг. |
521,74 |
85,892 |
-4,3396 |
0,404 |
-0,3511 |
|
Окончание табл. 3 |
|||||
|
Временной интервал |
С |
d1 |
d2 |
bz.1 |
bz.2 |
|
2001–2015 гг. |
509,91 |
91,372 |
-4,7745 |
0,157 |
-0,3573 |
|
2001–2016 гг. |
512,76 |
90,12 |
-4,6812 |
0,080 |
-0,2720 |
|
2001–2017 гг. |
519,05 |
87,512 |
-4,497 |
0,139 |
-0,3427 |
|
Модель NE3(t) |
|||||
|
2001–2015 гг. |
893,32 |
-9,7087 |
1,0276 |
0,161 |
-0,3623 |
|
2001–2016 гг. |
897,89 |
-11,709 |
1,1768 |
0,106 |
-0,1989 |
|
2001–2017 гг. |
904,76 |
-14,563 |
1,3778 |
0,118 |
0,1222 |
Таблица 4
Идентифицированные значения коэффициентов модели (10) NE3(t) для выделенных временных интервалов
|
Коэффициенты |
2001–2012 гг. |
2001–2013 гг. |
2001–2014 гг. |
|
a |
- 45,011 |
6,597 |
6,597 |
|
b |
1,055 |
0,997 |
0,997 |
Таблица 5
Значения статистических критериев, характеризующие построенные модели (1), (7), (10)
|
Временной интервал |
2001–2012 гг. |
2001–2013 гг. |
2001–2014 гг. |
2001–2015 гг. |
2001–2016 гг. |
2001–2017 гг. |
|
Модель NE1(t) (1) |
||||||
|
R2 |
0,843 |
0,874 |
0,868 |
0,857 |
0,871 |
0,862 |
|
Fрасч (FТ) |
19,571 (4,844) |
7,943 (4,747) |
5,890 (4,667) |
5,721 (4,600) |
5,126 (4,543) |
4,904 (4,494) |
|
KDW (d2) |
1,801 (1,023) |
2,010 (1,038) |
1,615 (1,034) |
1,616 (1,070) |
1,360 (1,086) |
1,286 (1,102) |
|
Модель LPр(t) (7) |
||||||
|
R2 |
0,9542 |
0,95 |
0,9427 |
0,9342 |
0,9317 |
0,9352 |
|
Fрасч (FТ) |
4,5434 (3,7082) |
4,655 (3,3258) |
4,7696 (3,8852) |
4,5768 (3,1791) |
4,7936 (3,1122) |
4,8276 (3,0555) |
|
KDW (d2) |
2,28 (1,913) |
2,18 (1,83) |
2,05 (1,826) |
1,86 (1,704) |
1,959 (1,663) |
2,045 (1,63) |
|
Модель NE3(t) (10) |
||||||
|
R2 |
0,861 |
0,921 |
0,913 |
0,8404 |
0,8699 |
0,8882 |
|
Fрасч (FТ) |
55,67 (4,1028) |
127,451 (3,8852) |
127,451 (3,8055) |
5,1184 (3,7389) |
4,9189 (3,6823) |
7,9651 (3,6337) |
|
KDW (d2) |
2,184 (1,274) |
2,030 (1,261) |
2,004 (1,234) |
1,719 (1,704) |
2,059 (1,663) |
1,909 (1,63) |
Исходная модель (10) NE3(t) для временных интервалов «2001–2015 гг.», «2001–2016 гг.», «2001–2017 гг.» не обеспечивала приемлемую точность – значения критерия R2 колебались в диапазоне от 0,574 до 0,732. Поэтому была использована модель по своей структуре аналогичная выражению (7). Именно для этой модели в табл. 5 приведены расчетные значения R2, Fрасч и KDW для данных временных интервалов, которые указывают на целесообразность использования более сложной модели (7) для описания NE3(t).
Таблица 6
Краткосрочный прогноз значений NE1(tf), 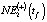 ,
, 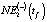 ,
,
NE3(tf), NE(+)(tf) и NE(-)(tf) для 2013–2018 гг. (тыс. чел.)
|
Год, tf |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
|
NE1(tf) |
896,93 |
915,07 |
933,62 |
921,71 |
1025,43 |
1024,4 |
|
|
838 152,64 |
830 692,17 |
829 862,30 |
821 231,74 |
803 205,37 |
804 811,78 |
|
|
834 836,50 |
823 223,41 |
825 712,99 |
817 125,58 |
797 995,48 |
796 399,49 |
|
|
931,52 |
945,03 |
985,26 |
1038,56 |
1061,60 |
1120,63 |
|
|
927,83 |
936,53 |
980,33 |
1033,37 |
1054,71 |
1108,91 |
|
NE3(tf) |
917,706 |
919,743 |
952,044 |
1023,39 |
1030,64 |
1091,81 |
|
|
915,38 |
926,61 |
956,97 |
994,55 |
1039,22 |
1078,95 |
|
|
914,16 |
923,78 |
955,33 |
992,82 |
1036,93 |
1075,04 |
В табл. 6 для tf с 2013 по 2018 г. совместно приведены расчетные значения NE1(tf) (1) и NE3(tf) (10) с учетом значений постоянных данных зависимостей, приведенных в табл. 2, 3, 4. Значения 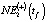 ,
, 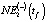 оценивались согласно (5) для значений
оценивались согласно (5) для значений 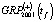 и
и 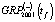 . Здесь же приведены и прогнозные значения NE(+)(tf) и NE(-)(tf), рассчитанные по зависимости (11). В табл. 7 приведены оценки
. Здесь же приведены и прогнозные значения NE(+)(tf) и NE(-)(tf), рассчитанные по зависимости (11). В табл. 7 приведены оценки 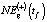 и
и 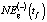 , собранные автором из официальных документов, размещенных на сайте (https://gov.admhmao.ru/plany/prognoz-sotsialno-ekonomicheskogo-razvitiya-khmao-yugry/) экономическим департаментом администрации ХМАО-Югры. В связи с тем, что в этих документах присутствует несколько прогнозных оценок для каждого года tf, в табл. 7 приведены те оценки, что наиболее близки к соответствующим фактическим данным.
, собранные автором из официальных документов, размещенных на сайте (https://gov.admhmao.ru/plany/prognoz-sotsialno-ekonomicheskogo-razvitiya-khmao-yugry/) экономическим департаментом администрации ХМАО-Югры. В связи с тем, что в этих документах присутствует несколько прогнозных оценок для каждого года tf, в табл. 7 приведены те оценки, что наиболее близки к соответствующим фактическим данным.
Таблица 7
Соотношение значений 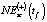 ,
, 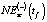 ,
, 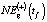 ,
, 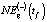 ,
, 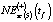 ,
,
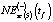 и NEst(t) для 2013–2018 гг.
и NEst(t) для 2013–2018 гг.
|
Год |
2013 |
2014 |
2015 |
2016 |
2017 |
2018 |
|
NEst(t) |
916,10 |
917,20 |
1037,40 |
1025,40 |
1077,90 |
1085,70 |
|
|
1184,52 |
916,10 |
918,40 |
919,78 |
921,16 |
1027,41 |
|
|
0,293 |
-0,001 |
-0,115 |
-0,103 |
-0,145 |
-0,054 |
|
|
1181,56 |
914,87 |
917,48 |
917,94 |
918,40 |
1026,49 |
|
|
0,290 |
-0,003 |
-0,116 |
-0,105 |
-0,148 |
-0,055 |
|
|
915,38 |
926,61 |
956,97 |
994,55 |
1039,22 |
1078,95 |
|
|
0,001 |
-0,010 |
0,078 |
0,030 |
0,036 |
0,006 |
|
|
914,16 |
923,78 |
955,33 |
992,82 |
1036,93 |
1075,04 |
|
|
0,002 |
-0,007 |
0,079 |
0,032 |
0,038 |
0,010 |
|
|
914,22 |
930,05 |
959,44 |
980,14 |
1043,51 |
1072,51 |
|
|
0,002 |
-0,014 |
0,075 |
0,044 |
0,032 |
0,012 |
|
|
912,38 |
925,80 |
956,98 |
977,54 |
1040,07 |
1066,66 |
|
|
0,004 |
-0,009 |
0,078 |
0,047 |
0,035 |
0,018 |
Наличие нескольких оценок обусловлено также и тем, что подразделения администрации, занимающиеся формированием прогнозов социально-экономического развития округа, работают с горизонтом прогнозирования в три года. Вследствие этого минимум один раз производится корректировка прогнозных значений с учётом изменяющихся условий функционирования региональной социально-экономической системы в целом. В табл. 7 также приведены значения 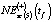 и
и 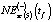 , рассчитанные по зависимости (5). Близость значений
, рассчитанные по зависимости (5). Близость значений 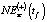 ,
, 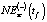 ,
, 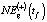 ,
, 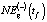 ,
, 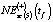 ,
, 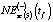 к NEst(t) определялась согласно зависимости (12).
к NEst(t) определялась согласно зависимости (12).
Анализ данных табл. 7 говорит о том, что более близкие к NEst(t) для региональной экономики ХМАО-Югры краткосрочные оценки величины 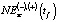 даёт использование комплексной модели (11). Это относится и к прогнозным оценкам
даёт использование комплексной модели (11). Это относится и к прогнозным оценкам 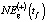 и
и 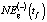 , формируемым профильными департаментами администрации округа. Наибольшая ошибка прогнозирования наблюдается в 2015 г., так как за этот год значение NEst(t) выросло более чем на 10 % по отношению к предыдущим двум годам. Похожих изменений величины NEst(t) не наблюдается как в предыдущем, так и в следующем за этим годом временным интервалах. Поэтому прогнозирование с использованием эконометрических моделей, идентификация которых осуществляется по ретроспективным данным NEst(t), не обеспечивает получение достаточно близких к фактическим данным результатов
, формируемым профильными департаментами администрации округа. Наибольшая ошибка прогнозирования наблюдается в 2015 г., так как за этот год значение NEst(t) выросло более чем на 10 % по отношению к предыдущим двум годам. Похожих изменений величины NEst(t) не наблюдается как в предыдущем, так и в следующем за этим годом временным интервалах. Поэтому прогнозирование с использованием эконометрических моделей, идентификация которых осуществляется по ретроспективным данным NEst(t), не обеспечивает получение достаточно близких к фактическим данным результатов 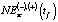 .
.
Заключение
Оценки среднегодовой численности занятых в региональной экономике, полученные в рамках краткосрочного прогнозирования с использованием комплекса эконометрических моделей, оперирующих ключевыми макроэкономическими показателями, характеризующими ее функционирование, достаточно близки к значениям этого экономического показателя, опубликованным органами государственной статистики. Повышение точности прогнозирования было осуществлено за счет интеграции в данный комплекс эконометрической модели, отражающей динамику рассматриваемого показателя. Вместе с тем следует отметить, что все полученные прогнозные значения ниже фактических значений численности занятых в региональной экономике ХМАО-Югры. Это обусловлено тем, что эконометрические модели идентифицируются на ретроспективных данных значений экономических показателей. При отсутствии в предшествующих временных интервалах значительных изменений значений наблюдаемого экономического показателя обеспечить в прогнозируемом интервале существенные изменения его значений, используя модели подобно типа, достаточно сложно.
Работа выполнена при поддержке гранта РФФИ и Правительства ХМАО-Югры на реализацию научного проекта № 18-47-860016 «Компьютерное моделирование динамики социально-экономической системы ресурсодобывающего региона севера России c использованием теории роста, агентного подхода и ГИС-технологий».
Библиографическая ссылка
Кутышкин А.В. КРАТКОСРОЧНОЕ ПРОГНОЗИРОВАНИЕ ЧИСЛЕННОСТИ ЗАНЯТЫХ В РЕГИОНАЛЬНОЙ ЭКОНОМИКЕ ХМАО-ЮГРЫ // Фундаментальные исследования. 2021. № 2. С. 30-37;URL: https://fundamental-research.ru/ru/article/view?id=42962 (дата обращения: 22.02.2026).
DOI: https://doi.org/10.17513/fr.42962