Не вызывает сомнений и является общепризнанным факт, что на принятие решений оказывают влияние социальные, эмоциональные, когнитивные факторы, которые находят свое отражение в сознании человека. Рефлексия является одним из фундаментальных свойств человеческого бытия. Соответственно, проблема адекватного описания механизма индивидуального выбора в ситуации взаимодействия несовпадающих интересов сторон является одной из центральных проблем экономико-математической науки.
Основателем теории рефлексных игр и пионером в изучении влияния рефлексии на индивидуальный выбор является советский и американский ученый, математик и психолог, Лефевр Владимир Александрович (род. 1936) [1]. Центральное место в исследованиях Лефевра занимают модели рефлексии и саморефлексии человека, отражающие акты поведения, нейронные механизмы и ментальные феномены. Лефевр ввел понятия рефлексивной системы, рефлексивной структуры и рефлексивного управления. В России ведущие позиции в области исследований рефлексивных игр занимают ученые Института проблем управления имени В.А. Трапезникова [2–4]. Рефлексивные игры применяются для анализа задач принятия решений с учетом взаимодействия интересов игроков, характера их взаимоотношений, в условиях различной информированности.
Рефлексивным управлением называется воздействие на субъектов, которое склоняет их принять решение, подготовленное управляющей стороной [1, с. 89]. Субъектами могут быть отдельные лица, объединения лиц, организации.
Цель исследования: включение в теоретико-игровой анализ рефлексивного управления показателя принадлежности к группе взаимодействующих субъектов в условиях нечеткого определения характера взаимоотношений между ними (конфронтации или союза).
Применяемые методы исследования – формализация и математизация проблемы рефлексивного управления индивидуальным выбором в группе взаимодействующих субъектов.
Результаты исследования и их обсуждение
Рассмотрим группу взаимодействующих субъектов S = {S1, S2,…, Sn}, каждый из которых, Si, i = 1, 2,…, n, является лицом, принимающим решения, (ЛПР). Для каждого субъекта Si может быть определено нечеткое множество
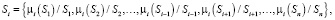 (1)
(1)
функция принадлежности которого характеризует уровень отношений субъектов Si и Sj, j = 1, 2, …, i – 1, i + 1,…, n. Будем предполагать, что для любых i и j справедливо условие:
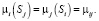 (2)
(2)
Функция μi(Sj) принимает значение 1, если субъекты Si и Sj находятся в отношениях союза в условиях полного доверия и открытости, что предполагает отсутствие какого-либо конфликта интересов между ними. Функция μi(Sj) принимает значение 0, если субъекты Si и Sj находятся в отношении конфронтации. Область допустимых значений функций μi(Sj), i = 1, 2,…, n, – отрезок [0; 1]. Чем ближе отношения субъектов Si и Sj к союзническим, соответственно, тем ближе значение функции μi(Sj) должно быть к единице.
Определим для нечеткого множества (1) четкое подмножество уровня γ. Параметр γ∈[0;1] имеет смысл критического уровня принадлежности, разделяющего для игрока Si, i = 1, 2,…, n, всех субъектов Sj, j = 1, 2,…, i – 1, i + 1,…, n, на две группы: условных союзников и условных противников:
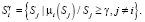 (3)
(3)
Каждому участнику Si группы S доступно множество элементарных действий:
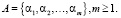 (4)
(4)
Любое подмножество совместных действий 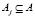 образует альтернативную стратегию (вариант решения) субъекта Si. Множество M всех подмножеств A образует множество альтернативных решений субъектов Si, i = 1, 2,…, n. Выбор альтернативы определяется интенцией (внутренним намерением) субъекта Si, а также его взаимоотношениями с другими субъектами в группе.
образует альтернативную стратегию (вариант решения) субъекта Si. Множество M всех подмножеств A образует множество альтернативных решений субъектов Si, i = 1, 2,…, n. Выбор альтернативы определяется интенцией (внутренним намерением) субъекта Si, а также его взаимоотношениями с другими субъектами в группе.
Для определенности предположим, что множество A включает элементы α1, α2, α3:
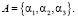 (5)
(5)
В этом случае множество альтернативных решений субъекта примет вид
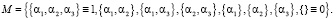 (6)
(6)
Для каждого субъекта Si определена функция Fi индивидуального выбора, определенная на множестве M [1, с. 36]:
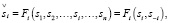 (7)
(7)
где 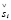 – выбор субъекта Si (значение функции выбора Fi);
– выбор субъекта Si (значение функции выбора Fi);
si – переменная функции выбора Fi, отражающая интенцию субъекта Si выбрать определенную альтернативу из множества M;
sj – переменная функции выбора Fi, альтернатива, к выбору которой субъект S j ≠ i склоняет субъекта Si.
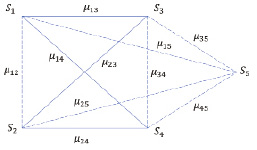
Рис. 1. Граф G1 отношений субъектов S1, S2, S3, S4, S5 при γ = γ1
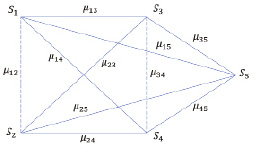
Рис. 2. Граф G2 отношений субъектов S1, S2, S3, S4, S5 при γ = γ2
Вид функции Fi, i = 1, 2,…, n, задается графом G отношений в группе и соответствующим ему полиномом. Узлы графа соответствуют субъектам, а ребра характеризуют отношения между субъектами.
Проиллюстрируем процесс построения полинома и функции индивидуального выбора на конкретном примере. Сравним графы отношений субъектов G1 с критическим уровнем принадлежности γ = γ1 и G2 с критическим уровнем принадлежности γ = γ2, предполагая для определенности, что γ11 > γ2.
Предположим, при γ = γ1 граф G1 отношений субъектов в группе имеет вид (рис. 1).
При γ = γ2 получаем граф отношений G2 (рис. 2).
Отношениям союза на рис. 1 и 2 соответствуют ребра графов, представленные сплошной линией, отношениям конфликта – ребра графов, обозначенные пунктирной линией.
В отличие от графа G1 граф G2 предполагает союзнические взаимоотношения субъекта S5 с другими субъектами группы. То есть для графа G1, справедливы соотношения
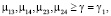 (8)
(8)
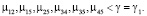 (9)
(9)
Для графа G2:
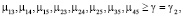 (10)
(10)
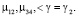 (11)
(11)
Граф G2 показывает, что при понижении критического уровня принадлежности γ к группе союзников игроков до уровня γ2 субъект S5 рассматривается в группе как союзник для каждого из субъектов: S1, S2, S3, S4.
Графу G1 соответствует полином
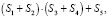 (12)
(12)
графу G2:
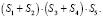 (13)
(13)
Функции индивидуального выбора субъектов группы, соответствующие графам G1 и G2, представлены в табл. 1.
Таблица 1
Функции индивидуального выбора
|
Граф отношений G1 |
Граф отношений G2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2
Матрица P взаимных влияний нецеленаправленных субъектов
|
Субъект |
S1 |
S2 |
S3 |
S4 |
S5 |
|
S1 |
{α1, α2} |
{} |
{α1, α3} |
{α3} |
{α1, α2} |
|
S2 |
{α1} |
{α1, α3} |
{} |
{α1, α2, α3} |
{α2, α3} |
|
S3 |
{α2, α3} |
{α2} |
{α1} |
{α1, α2} |
{} |
|
S4 |
{α3} |
{α1, α2} |
{α3} |
{α2, α3} |
{α3} |
|
S5 |
{α2} |
{} |
{α1, α2, α3} |
{} |
{α1} |
Общая схема решения задачи индивидуального выбора в рамках теории рефлексивных игр Лефевра может быть представлена в виде последовательности шагов [1, с. 42–44]:
1. Определяется группа субъектов S = {S1, S2,…, Sn}, n > 1.
2. Для любой пары субъектов группы S задается отношение союза или конфликта.
3. Взаимоотношения субъектов в группе представляются в виде графа G.
4. Задается набор действий A = {α1, α2,…, αm}, любая реализуемая комбинация которых определяет альтернативу индивидуального выбора.
5. Строится матрица воздействий (влияний) P = pij, элемент pij которой отражает желательный с позиции субъекта Si выбор субъектом Sj, i, j = 1, 2,…, n. Элемент pii имеет смысл выбора, желаемого самим субъектом Si.
6. На основе графа G строится полином, отношению союза в котором соответствует операция логического умножения, а отношению конфликта – операция логического сложения.
7. Полином графа G определяет вид функции индивидуального выбора (7) для каждого субъекта.
8. Если субъект является целенаправленным, т.е. способным реализовать свои интенции, то в функции (7) переменная интенции 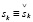 полагается неизвестной, тождественно равной переменной выбора. В случае нецеленаправленного субъекта выбор субъекта Sk полностью определяется системой отношений внутри группы, в которую он входит.
полагается неизвестной, тождественно равной переменной выбора. В случае нецеленаправленного субъекта выбор субъекта Sk полностью определяется системой отношений внутри группы, в которую он входит.
9. Далее решается уравнение индивидуального выбора для каждого субъекта с учетом матрицы воздействий P.
Предположим, субъекты S1, S2,…, S5 не являются целенаправленными, и матрица P взаимных воздействий (влияний) имеет вид (табл. 2).
Нецеленаправленным субъектом является игрок, выбор которого подчиняется внешнему влиянию и может не совпадать с внутренним намерением выбрать определенную альтернативу. Для целенаправленного игрока интенция и реальный выбор совпадают [1, с. 36].
Подставим управляющие воздействия из матрицы (табл. 2) в уравнения (14.1)–(14.5), предполагая систему взаимоотношений G1:
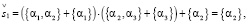 (16.1)
(16.1)
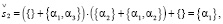 (16.2)
(16.2)
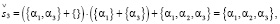 (16.3)
(16.3)
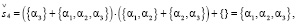 (16.4)
(16.4)
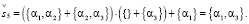 (16.5)
(16.5)
В случае графа G2 используется система уравнений (15.1)–(15.5):
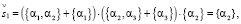 (17.1)
(17.1)
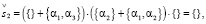 (17.2)
(17.2)
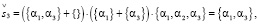 (17.3)
(17.3)
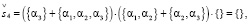 (17.4)
(17.4)
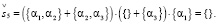 (17.5)
(17.5)
Таблица 3
Интенции и реальный выбор нецеленаправленных субъектов
|
Субъект |
Интенция |
Индивидуальный выбор (Граф G1) |
Индивидуальный выбор (Граф G2) |
|
S1 |
{α1, α2} |
{α2} |
{α2} |
|
S2 |
{α1, α3} |
{α1} |
{} |
|
S3 |
{α1} |
{α1, α2, α3} |
{α1, α3} |
|
S4 |
{α2, α3} |
{α1, α2, α3} |
{} |
|
S5 |
{α1} |
{α1, α3} |
{} |
Таблица 4
Матрица P взаимных влияний целенаправленных субъектов
|
Субъект |
S1 |
S2 |
S3 |
S4 |
S5 |
|
S1 |
s1 |
{} |
{α1, α3} |
{α3} |
{α1, α2} |
|
S2 |
{α1} |
s2 |
{} |
{α1, α2, α3} |
{α2, α3} |
|
S3 |
{α2, α3} |
{α2} |
s3 |
{α1, α2} |
{} |
|
S4 |
{α3} |
{α1, α2} |
{α3} |
s4 |
{α3} |
|
S5 |
{α2} |
{} |
{α1, α2, α3} |
{} |
s5 |
Сравним интенции и реальный выбор нецеленаправленных субъектов, корректирующих свои решения под влиянием других субъектов в группе с учетом конфигурации взаимоотношений в группе (табл. 3).
Ни один из пяти рассматриваемых субъектов не смог реализовать свои интенции и вынужден был скорректировать свой выбор под влиянием других субъектов.
Предположим теперь, что субъекты целенаправленны. В этом случае диагональные элементы матрицы P не известны и задача фактически заключается в поиске таких решений, которые могут быть реализованы при заданной композиции взаимоотношений в группе.
Матрица взаимных влияний субъектов примет вид (табл. 4).
В случае целенаправленных субъектов уравнение индивидуального выбора следует переписать в виде [1, с. 16]:
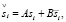 (18)
(18)
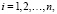
где A и B не зависят от si.
Уравнение (18) будет иметь решение тогда и только тогда, когда
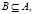 (19)
(19)
и решения уравнения (18) удовлетворяют условию
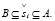 (20)
(20)
Для графа отношений G1 решения уравнений (18) выведены в работе [5, с. 54]. Полученные варианты выбора целенаправленных субъектов Si, i = 1, 2,…,5, совпадающие с их интенциями, имеют вид
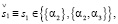 (21.1)
(21.1)
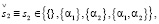 (21.2)
(21.2)
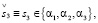 (21.3)
(21.3)
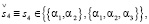 (21.4)
(21.4)
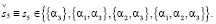 (21.5)
(21.5)
Решим уравнения (18) для целенаправленных субъектов Si, i = 1, 2,…,5, с композицией взаимоотношений, представленной графом G2.
Уравнение для субъекта S1:
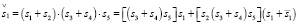 =
=
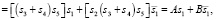 (22.1)
(22.1)
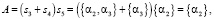
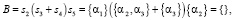
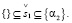 (22.2)
(22.2)
Из (22.2) следует, что субъекту S1 доступны два альтернативных решения:
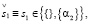 (22.3)
(22.3)
совпадающие с его интенциями.
Уравнение для субъекта S2:
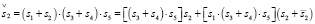
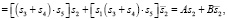 (23.1)
(23.1)
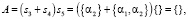
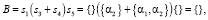
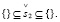 (23.2)
(23.2)
Субъект S2 может реализовать свою интенцию бездействия:
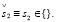 (23.3)
(23.3)
Уравнение для субъекта S3:
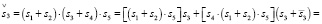
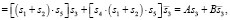 (24.1)
(24.1)
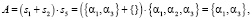
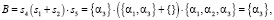
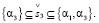 (24.2)
(24.2)
Следовательно, субъекту S3 доступны решения
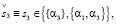 (24.3)
(24.3)
совпадающие с его интенциями.
Уравнение для субъекта S4:
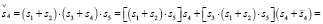
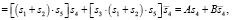 (25.1)
(25.1)
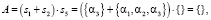
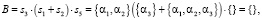
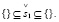 (25.2)
(25.2)
Субъект S4 имеет возможность реализовать интенцию, не связанную с выбором какой-либо не пустой альтернативы:
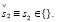 (25.3)
(25.3)
Уравнение для субъекта S5:
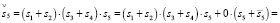
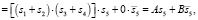 (26.1)
(26.1)
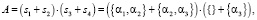
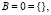
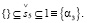 (26.2)
(26.2)
Субъекту S5 доступны решения
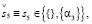 (26.3)
(26.3)
совпадающие с его интенциями.
Сопоставим влияния на субъектов Si, i = 1,2,…,5, со стороны других субъектов группы с вариантами их выбора (табл. 5–9).
Таблица 5
Влияние на субъекта S1 и его выбор
|
Влияющий субъект |
Влияние |
Варианты индивидуального выбора S1 (граф G1) |
Варианты индивидуального выбора S1 (граф G2) |
|
S2 |
{α1} |
{α2}, {α2, α3} |
{}, {α2} |
|
S3 |
{α2, α3} |
||
|
S4 |
{α3} |
||
|
S5 |
{α2} |
Таблица 6
Влияние на субъекта S2 и его выбор
|
Влияющий субъект |
Влияние |
Варианты индивидуального выбора S2 (граф G1) |
Варианты индивидуального выбора S2 (граф G2) |
|
S1 |
{} |
{}, {α1}, {α2}, {α1, α2} |
{} |
|
S3 |
{α2} |
||
|
S4 |
{α1, α2} |
||
|
S5 |
{} |
Таблица 7
Влияние на субъекта S3 и его выбор
|
Влияющий субъект |
Влияние |
Варианты индивидуального выбора S3 (граф G1) |
Варианты индивидуального выбора S3 (граф G2) |
|
S1 |
{α1, α3} |
{α1, α2, α3} |
{α3}, {α1, α3} |
|
S2 |
{} |
||
|
S4 |
{α3} |
||
|
S5 |
{α1, α2, α3} |
Таблица 8
Влияние на субъекта S4 и его выбор
|
Влияющий субъект |
Влияние |
Варианты индивидуального выбора S4 (граф G1) |
Варианты индивидуального выбора S4 (граф G2) |
|
S1 |
{α3} |
{α1, α2}, {α1, α2, α3} |
{} |
|
S2 |
{α1, α2, α3} |
||
|
S3 |
{α1, α2} |
||
|
S5 |
{} |
Таблица 9
Влияние на субъекта S5 и его выбор
|
Влияющий субъект |
Влияние |
Варианты индивидуального выбора S5 (граф G1) |
Варианты индивидуального выбора S5 (граф G2) |
|
S1 |
{α1, α2} |
{α3}, {α1, α3}, {α2, α3}, {α1, α2, α3} |
{}, {α3} |
|
S2 |
{α2, α3} |
||
|
S3 |
{} |
||
|
S4 |
{α3} |
Согласно табл. 5–9 изменение критического уровня принадлежности группе союзников γ привело к изменению возможных под влиянием внешних управляющих воздействий вариантов выбора решений для каждого из субъектов Si, i = 1, 2,…, n. При различных значениях γ будут иметь место различные варианты индивидуального выбора игроков в ситуации, когда корректировка параметра γ влечет за собой изменение конфигурации отношений в группе. При γ = 0 получаем группу субъектов в отношениях союза на условиях полного доверия и открытости. При γ = 1 – группу субъектов в отношениях полной конфронтации. Такие группы субъектов называют суперактивными [1, с. 67–70]. Можно показать, что в случае суперактивной группы любой субъект выберет альтернативу 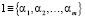 . Таких субъектов, соответственно, называют суперактивными.
. Таких субъектов, соответственно, называют суперактивными.
Заключение
Рассмотренные выше условные примеры рефлексивного взаимодействия субъектов соответствуют ситуациям управления выбором игроков через взаимное манипулирование посредством прямого влияния и путем изменения отношений (через повышение или понижение критического уровня принадлежности к группе союзников γ).
На выбор игрока (субъекта Si) не оказывает непосредственное влияние уровень принадлежности μi(Sj) субъектов Sj к группе союзников данного игрока до тех пор, пока неизменным сохраняется соотношение μi(Sj) и γ для любого j = 1, 2,…, i –1, i + 1,…, n. Имеет значение конкретная конфигурация отношений, определяемая параметром γ. И целенаправленные, и нецеленаправленные субъекты, определяя желаемые исходы противостояния интересов, задают условную границу γ и, сравнивая μi(Sj) и γ, разделяют игроков на союзников и противников. Другими словами, именно результаты выбора игроками Si, i = 1, 2,…, n, (с учетом взаимного влияния в условиях конфликта интересов) своих действий и соответствие этих результатов целям игрока указывают на истинный (наиболее адекватный ситуации) критический уровень принадлежности γ субъектов Sj, j = 1, 2,…, i –1, i + 1,…, n, к группе союзников игрока Si, i = 1, 2,…, n.
Библиографическая ссылка
Михалева М.Ю. МОДЕЛИРОВАНИЕ РЕФЛЕКСИВНОГО ВЗАИМОДЕЙСТВИЯ СТОРОН В УСЛОВИЯХ КОНФЛИКТА ИНТЕРЕСОВ // Фундаментальные исследования. 2019. № 5. С. 69-77;URL: https://fundamental-research.ru/ru/article/view?id=42463 (дата обращения: 10.03.2026).




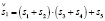 (14.1)
(14.1)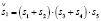 (15.1)
(15.1)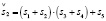 (14.2)
(14.2)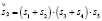 (15.2)
(15.2)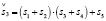 (14.3)
(14.3)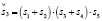 (15.3)
(15.3)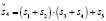 (14.4)
(14.4)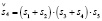 (15.4)
(15.4)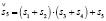 (14.5)
(14.5)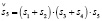 (15.5)
(15.5)