Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Носова М.Г. 1

---

1 ФГБОУ ВО «Томский государственный университет систем управления и радиоэлектроники»

В этой статье предложена математическая модель изменения численности клиентов компании по микрофинансированию со смешанными потоками входящих рисков. Такая компания по микрофинансированию специализируется на двух видах кредитования, например простой займ и пенсионный займ. В качестве математической модели выбрана бесконечно-линейная система массового обслуживания M|M|∞ с неограниченным числом обслуживающих приборов, с простейшими входящими потоками заявок и экспоненциальным временем обслуживания их на приборах. Деятельность компании определяется двумя случайными процессами: числом заключенных кредитных договоров и капиталом компании. Исследование этих двух процессов выполнено методами теории массового обслуживания. Получена система дифференциальных уравнений, определяющая распределение вероятностей числа пришедших клиентов и числа заключенных договоров в системе массового обслуживания. Найден вид характеристической функции величины изменения капитала компании по микрофинансированию. Методом моментов найдены основные вероятностные характеристики капитала компании: математическое ожидание и дисперсия.

Статья в формате PDF

0 KB

система массового обслуживания

компания по микрофинансированию

собственный капитал

M|M|?

1. Носова М.Г., Тивякова М.В. Математическая модель компании по микрокредитованию в виде системы массового обслуживания // Материалы Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых (Томск, 13–15 мая 2015 г.). – Томск, 2015. – Ч. 4. – С. 304–305.

2. Моисеев А.П., Сергеев А.Е. Математическая модель страховой компании в виде СМО с неограниченным числом обслуживающих приборов // Научное творчество молодежи: материалы XVI Всероссийской научно-практической конференции (Анжеро-Судженск, 17–18 мая 2012 г.). – Анжеро-Судженск, 2012. – Ч. 1. – С. 37–38. URL: http://www.asf.ru/upload/sbornikNTM-2012-ch1.pdf (дата обращения: 01.11.2017).

3. Назаров А.А. Теория массового обслуживания: Учебное пособие / А.А. Назаров, А.Ф. Терпугов. – Томск: Изд-во НТЛ, 2004. – 228 с.

4. Клейнрок Л. Теория массового обслуживания / Л. Клейнрок. – М.: Книга по Требованию, 2013. – 429 с.

5. Зорин A.B., Федоткин М.А. Оптимизация управления дважды стохастическими неординарными потоками в системах с разделением времени / А.В. Зорин, М.А. Федоткин // Автоматика и телемеханика. – 2005. – № 7. – С. 102–111.

6. Назаров А.А., Носова М.Г. Математическая модель процесса изменения демографической ситуации и ее исследование // Доклады Томского государственного университета систем управления и радиоэлектроники. – 2009. – Т. 2 (20). – С. 100–105.

В настоящее время развивающимся направлением в России является микрофинансирование. Востребованность микрофинансирования и доступность открытия компании делают этот сегмент кредитования весьма привлекательным для создания собственного бизнеса. В этих условиях большое значение приобретает исследование вопросов микрофинансирования. Одним из таких вопросов является оценка минимального размера создаваемого капитала компании и прогнозирование динамики капитала с учетом возможных рисков. Ведь собственный капитал является базовым показателем при расчете нормативов деятельности кредитной организации, установленных Банком России, и одним из ориентиров для оценки бизнеса рынком, а следовательно, и инвесторами [1].

Кредитование как отрасль экономики, связана с риском случайных финансовых потерь (невозвратом долга), которые возникают в результате нежелательных событий, например потеря трудоспособности, болезнь, смерть и т.п. Основной принцип любого кредитования состоит в том, что кредитор (банк) выдает заемщику определенную денежную сумму на определенный срок под определенный процент, а заемщик обязуется вернуть денежную сумму на оговоренных условиях. В результате некоторых нежелательных событий заемщик не возвращает сумму, в этом случае кредитор несет финансовые потери.

Хотя для каждого кредитного договора значения денежной суммы (кредита) и возможной выплаты с учетом процентов строго оговорены, до момента заключения кредитного договора они неизвестны и должны рассматриваться как случайные величины. Моменты заключения новых кредитных договоров и наступления выплат по кредитам также являются случайными величинами.

Математическое моделирование является мощным и эффективным инструментом исследования таких вопросов и позволяет найти основные характеристики, а также построить научно обоснованные прогнозы величины капитала компании.

В работе для построения математической модели предлагается применить модели и методы теории массового обслуживания. Рассмотрим классическую бесконечно-линейную систему массового обслуживания M|M|∞ с неограниченным числом обслуживающих приборов, с простейшими входящими потоками заявок и экспоненциальным временем обслуживания их на приборах [2, 3].

Указанную систему массового обслуживания можно рассматривать как математическую модель потока клиентов некоторой компании по микрофинансированию, специализирующейся на двух видах кредитования, например простой займ и пенсионный займ [1]. Кредит выдается одной суммой, возврат кредита должен быть произведен в течение определенного срока, выплата процентов за использование кредитом происходит регулярно, процентная ставка фиксированная. Тогда приходящие заявки целесообразно разделить на две группы, каждая из которых обслуживается определённым образом.

На вход системы M|M|∞ поступает смешанный поток, состоящий из двух простейших потоков (стационарный пуассоновский) договоров с параметрами λ1 и λ2 соответственно. Договоры 1-го типа поступают в первый блок обслуживания, 2-го типа – во второй блок обслуживания и занимают любой из свободных приборов, на котором выполняется их обслуживание в течение случайного времени, распределённого по экспоненциальному закону с параметрами μ1 и μ2 соответственно.

Деятельность компании по микрофинансированию можно охарактеризовать двумя случайными величинами: числом заключенных кредитных договоров k(t) и капиталом компании S(t). Будем считать, что потенциальный рынок кредитных услуг считается бесконечным.

Рассмотрим процесс изменения состояний случайных процессов k(t) и S(t) с течением времени t. Изменение числа кредитных договоров и значений капитала компании происходит в следующих случаях.

1. Компания по микрофинансированию заключает новый кредитный договор и выдает денежную сумму. Будем предполагать, что поток заключенных кредитных договоров состоит из двух простейших потоков с параметрами λ1 и λ2. Очевидно, что заключение кредитного договора и выдача денежной суммы связаны с риском для компании. Вероятность того, что за время Δt компания примет на себя новый риск в зависимости от типа договора, равна 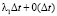и 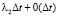. Каждый новый риск для компании связан с выдачей денежной суммы заемщику. φ1 и φ2 – размеры для первого и второго вида кредитования, которые являются случайными величинам с функциями распределения , и моментами , , , .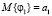

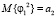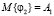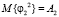2. По каждому из k1 заключенных кредитных договоров первого типа с интенсивностью 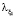выплачивается взнос по кредиту в размере ξ1, который является случайной величиной с функцией распределения 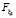и моментами 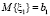, 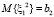. Выплаты вносятся независимо друг от друга, и поэтому за время Δt в компанию по микрофинансированию поступит такой взнос с вероятностью 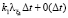. Аналогично по каждому из k2 заключенных кредитных договоров второго типа с интенсивностью 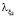выплачивается взнос по кредиту в размере ξ2, который является случайной величиной с функцией распределения 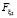и моментами 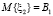, 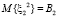. Выплаты вносятся независимо друг от друга, и поэтому за время Δt в компанию по микрофинансированию поступит такой взнос с вероятностью .

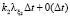3. В какой-то момент срок кредитного договора заканчивается. Будем считать, что срок, на который заключается кредитный договор, является случайной величиной с функцией распределения 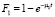для первого типа и 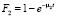для второго типа. Каждый кредитный договор расторгается и «покидает» компанию, независимо от срока действия других кредитных договоров, с интенсивностями μ1 и μ2. Тогда за время Δt кредитные договоры «покидают» компанию с вероятностям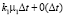и и 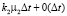соответственно.

4. Будем предполагать, что с каждым кредитным договором первого вида может наступить случай невозврата кредита с интенсивностью 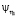. Эти случаи для различных кредитных договоров независимы. С вероятностью 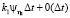наступают случаи невозврата кредита, где η1 – финансовые убытки компании. Размер η1 – является случайной величиной с функцией распределения 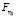и моментами 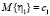, 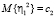. Аналогично, с каждым кредитным договором второго вида может наступить случай невозврата кредита с интенсивностью 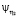. Эти случаи для различных кредитных договоров независимы. С вероятностью 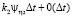наступают случаи невозврата кредита, где η2 – финансовые убытки компании. Размер η2 является случайной величиной с функцией распределения 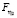и моментами , .

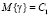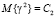Определим l1(t) и l2(t) как случайные процессы, которые характеризует число пришедших клиентов за время t за кредитами первого типа и второго типа, а i1(t) и i2(t) – число заключенных кредитных договоров каждого вида (выданных кредитов) в момент времени t.

Задача исследования данной математической модели состоит в нахождении распределения вероятностей

.

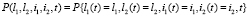Составим Δt-методом прямую систему дифференциальных уравнений Колмогорова [3, 4]:

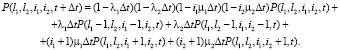
Откуда получаем систему дифференциальных уравнений:

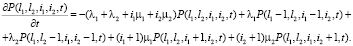(1)

Чтобы решить систему дифференциальных уравнений (1), определим производящую функцию четырехмерного распределения 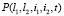в виде

.

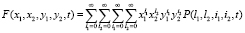Для производящей функции 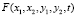из (1) получим обыкновенное дифференциальное уравнение в частных производных 1-го порядка следующего вида

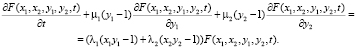
Откуда найдем выражение для производящей функции :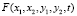

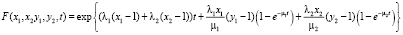. (2)

В результате определен вид производящей функции четырехмерного распределения .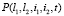

Из [5] известно, что капитал любой компании по микрофинансированию в определенный момент времени определяется следующим выражением:

,

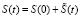где S(0) – начальный капитал.

Изменение капитала компании по микрофинансированию можно описать выражением

.

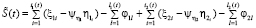Рассмотрим характеристическую функцию величины изменения капитала компании по микрофинансированию, полученного за время t. Очевидно, что

.

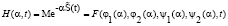Согласно виду производящей функции (2) найдем, что

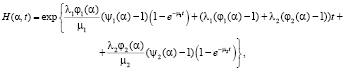(3)

где 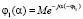– характеристическая функция величины 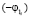, 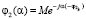– характеристическая функция величины 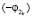, 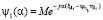– характеристическая функция величины 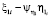, 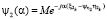– характеристическая функция величины 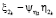, j – мнимая единица.

Среднее значение величины изменения капитала компании по микрокредитованию, полученного за время t, можно определить как

.

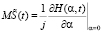Учитывая, что

,

,

,

,

.

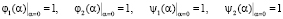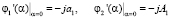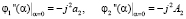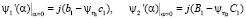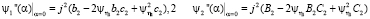Тогда методом моментов из (3) получим основные вероятностные характеристики [3, 6] капитала компании по микрофинансированию: математическое ожидание (среднее значение) и дисперсия:

,

,

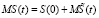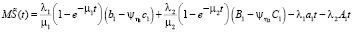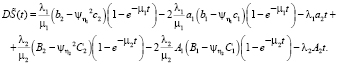
Заключение

1. Построена математическая модель изменения численности клиентов компании по микрофинансированию со смешанными потоками входящих рисков в виде системы массового обслуживания с неограниченным числом обслуживающих приборов (M|M|∞).

2. Получена система дифференциальных уравнений, определяющая распределение вероятностей числа пришедших клиентов и числа заключенных договоров в системе массового обслуживания.

3. Найден вид характеристической функции величины изменения капитала компании по микрофинансированию.

4. Методом моментов найдены основные вероятностные характеристики капитала компании: математическое ожидание и дисперсия.

Библиографическая ссылка