Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Наумова Н.А. 1 Домбровский А.Н. 1

---

1 ФГБОУ ВО «Кубанский государственный технологический университет»

Обострение транспортных проблем особенно заметно в узловых точках улично-дорожной сети. К преимуществам кольцевых пересечений в одном уровне относятся: снижение потерь времени на пересечении, лучшие условия выполнения разворота и левого поворота, ликвидация конфликта встречных потоков, большая пропускная способность, снижение аварийности. Неравномерность движения автотранспорта сказывается на степени эффективнoсти организации движения в местах пересечения транспортных потоков, в том числе и на кольцевых пересечениях. Разработана авторская математическая модель движения транспортных средств на кольцевых пересечениях, в котором кольцевое пересечение рассматривается как совокупность конфлитктных точек и дуг между ними. Предложены методы оценки транспортных затрат при различных схемах организации движения на кольцевых пересечениях. Разработан метод динамического определения наиболее эффективного способа организации движения на кольцевом пересечении в условиях функционирования интеллектуальных транспортных систем.

Статья в формате PDF

0 KB

кольцевое пересечение

организация движения

математическая модель

динамическое управление

1. Липницкий А.С. Современные кольцевые пересечения / А.В. Зедгенизов, Р.Ю. Лагерев, А.Г. Левашев, А.С. Липницкий, А.Ю. Михайлов, М.И. Шаров // Иркутский-государственный технический университет. – Иркутск, 2009. – 106 с.

2. Свод правил по проектированию геометрических элементов автомобильных дорог и транспортных пересечений. Часть 2: Свод правил по проектированию геометрических элементов транспортных пересечений автомобильных дорог // Федеральное дорожное агентство (Росавтодор). – М., 2013. – 212 с.

3. Flannery A., Kharoufeh J.P., Gautam and Elefteriadou L. Queuing delay models for singl-lane roundabouts // Civil Engineering and Environment Systems. – 2008. – Vol. 22, No. 3. – Р. 1333–150.

4. Robinson B.W. and other. Roundabouts: An Informational Guide // U.S. Department of Transportation. – Publication No. FHWA-RD-00-067. – 2010. – P. 284.

5. Поздняков М.Н. Совершенствование организации дорожного движения на кольцевых пересечениях: дис. ... канд. техн. наук: 05.22.10. – Ростов н/Д, 2005. – 164 с.

6. Наумова Н.А., Данович Л.М., Карачанская Т.А. Аналитическая модель движения автотранспортных средств на кольцевых пересечениях // Фундаментальные исследования. – 2016. – № 6–1. – С. 94–97.

7. Naumova N.A. Method for Estimating An Origin-Destination Matrix for Dynamic Assignment // International Journal of Control Theory and Applications. – 2016. – Vol. 9 (30). – Р. 129–138.

Обострение транспортных проблем, вызванное увеличением интенсивности движения автомобилей, особенно заметно в узловых точках сети и проявляется в росте величины задержек транспортных средств, в появлении заторов, излишнем расходе топлива, ухудшении экологической ситуации, снижении безопасности движения. С целью повышения безопасности движения и увеличения пропускной способности в двадцатых годах прошлого столетия в зарубежных странах начали устраивать кольцевые пересечения [1]. В 1960-х годах первые кольцевые пересечения появились и в СССР. К преимуществам кольцевых пересечений в одном уровне можно отнести, например, снижение потерь времени на пересечении, лучшие условия выполнения разворота и левого поворота, ликвидация конфликта встречных потоков, большая пропускная способность, снижение аварийности.

Существуют различные типы кольцевых пересечений и различные схемы организации движения на них [2]. Исследования в этой области проводятся как зарубежными [3, 4], так и российскими учеными [5]. В большинстве случаев существующая архитектурная застройка городов не позволяет менять планировочные решения. Однако неравномерность движения автотранспорта сказывается на степени эффективности организации движения в местах пересечения транспортных потоков, в том числе и на кольцевых пересечениях. И повлиять на эту ситуацию можно с помощью изменения организации движения по мере необходимости. Соверешенствование схем организации движения позволяет находить решение транспортных проблем без больших материальных зартат.

Развитие автоматизированных систем управления дорожным движением в рамках интеллектуальных транспортных систем (ИТС) дает возможность в режиме on-line реагировать на изменение дорожной ситуации.

Математическая модель движения транспортных средств на кольцевых пересечениях

Существуют две основные группы моделей кольцевых пересечений: эмпирические и аналитические (вероятностные). Эмпирический подход основан на получении регрессионных моделей, которые оценивают пропускную способность второстепенного направления по экспериментальным данным об интенсивности главного потока. Регрессионные модели применяют в Великобритании и ФРГ.

Аналитические методы по виду распределения интервалов между автомобилями в потоке, используя аппарат теории вероятностей и теории случайных процессов, определяют средние характеристики качества организации движения на кольцевом пересечении. Их применяют, например, в США, Австралии, Финляндии.

В работе [6] авторами предложена аналитическая модель движения транспортных средств на кольцевом пересечении в одном уровне, которая включена в общую модель TIMeR_Mod (Transportation Intelligent Mesoscopic Real-time Model). Базовой гипотезой для разработки модели явяляется гипотеза о распределении интервалов по времени между транспортными средствами по обобщенному закону Эрланга. Авторами было экспериментально доказано, что эмипирическое распределение интервалов в транспортном потоке хорошо согласуется с этим распределением при широком диапазоне интенсивностей.

Кольцевое пересечение в модели TIMeR_Mod рассматривается как совокупность конфликтных точек и дуг между ними. В случае кольцевого саморегулируемого движения на кольце средняя задержка (в секундах) в каждой конфликтной точке одного транспортного средства выбранного второстепенного направления A с учетом очереди равна

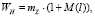(1)

где

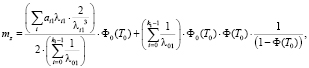
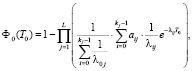
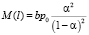– среднее число автомобилей в очереди, (2)

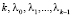– параметры обобщенного закона Эрланга для выбранного потока A, входящего в конфликтную точку;

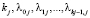– параметры обобщенного закона Эрланга для каждого из L конфликтных для потока A транспортных потоков;

Т0 – приемлемый временной интервал между автомобилями в конфликтных потоках для продолжения движения транспортными средствами потока A.

Все необходимые для расчетов данные содержатся в матрицах ASTREETS и BINTERSECTION модели TIMeR_Mod.

Для определения времени прохождения транспортным средством кольцевого пересечения с помощью модели TIMeR_Mod необходимо иметь следующие данные:

– количество въездов на кольцо (A, B, C, D,… – по часовой стрелке);

– организация движения (вариант 1–4);

– скорость движения на кольце;

– на векторах AB, BC, CD,... : количество полос, интенсивность; главное или второстепенное движение.

Ниже приведены варианты построения функции транспортных затрат на кольце при различных схемах организации движения [2] на нем для наиболее часто встречающейся ситуации пересечения двух дорог:

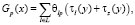(3)

где τ_l(y) – затраты на прохождение дуги y между двумя конфликтными точками, 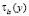= – средняя задержка в данной конфликтной точке.

Вариант 1. Организация движения с предоставлением преимущественного права проезда транспортным средствам, движущимся по кольцевой проезжей части.

Конфликтная точка – точка слияния потоков на въезде на кольцо. Главное направление – движение по кольцу. Для определения величины τ_lz(y) применяется разработанный авторами аналитический аппарат (формула (1) для узловой точки I типа – нерегулируемое пересечение).

Величина τ_l(y) рассчитывается следующим образом (с точностью до обозначений, А – точка въезда на кольцо):

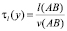– поворот направо;

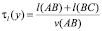– движение прямо;

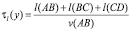– поворот налево.

Здесь приняты следующие обозначения: l(M1M2) – длина участка M1M2; v(M1M2) – скорость на участке M1M2.

Вариант 2. Организация движения с предоставлением преимущественного права проезда по одной из пересекающихся дорог. Главная дорога проходит в прямом направлении.

Пусть с точностью до обозначений, А – точка въезда на кольцо. Тогда функция транспортных затрат определяется следующим образом:

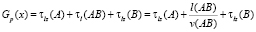– – при повороте направо;

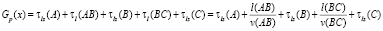– – при движении прямо;

–

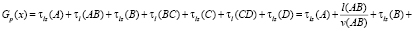
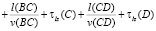– при повороте налево.

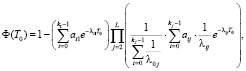
Величина τ_lz(y) равна нулю, если движение транспортного средства проходит по главному направлению. Если по второстепенному, то τ_lz(y) рассчитывается по формуле (1) для узловой точки I типа (нерегулируемое пересечение требований).

Вариант 3. Ни одно из направлений движения не выделено как главное. Водители должны руководствоваться «Правилами дорожного движения» и уступать дорогу транспортным средствам, приближающимся справа. По этому варианту организации движения приоритетом в движении в зоне слияния кольцевых пересечений пользуется поток, входящий на пересечение.

В этом случае въезд на кольцо – без задержек. Пусть опять с точностью до обозначений, А – точка въезда на кольцо. Тогда функция транспортных затрат определяется следующим образом:

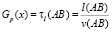– – при повороте направо;

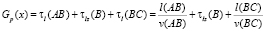– – при движении прямо;

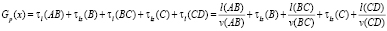– – при повороте налево.

Вариант 4. Организация движения на кольцевом пересечении, когда главная дорога изменяет свое направление. Этот вариант организации движения на кольцевых пересечениях применяется сравнительно редко.

В данном случае схема расчетов аналогична варианту 2. А – точка въезда на кольцо (с точностью до обозначений). Тогда функция транспортных затрат определяется следующим образом:

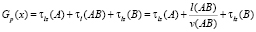– – при повороте направо;

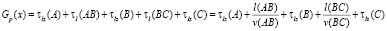– – при движении прямо;

–

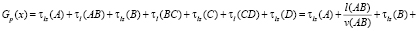
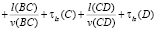– при повороте налево.

Величина τ_lz(y) равна нулю, если движение транспортного средства проходит по главному направлению. Если по второстепенному, то τ_lz(y) рассчитывается по формуле (1).

Варианты 1 и 3 организации движения также укладываются в схему расчетов для вариантов организации движения 2 и 4. Поэтому при составлении базы данных, описывающей кольцевое пересечение, достаточно указывать пункт «– на векторах AB, BC, CD,... : количество полос, параметры распределения обобщенного закона Эрланга для интервалов; главное или второстепенное движение».

Управление в динамическом режиме

Для обеспечения эффективной организации движения недостаточно иметь автомобильную дорогу с заданными техническими характеристиками и оборудованную необходимой дорожной информацией. Необходима кроме этого гибкая система управления, позволяющая реагировать на изменения в режиме движения и прогнозировать оптимальные схемы организации движения транспортных средств. Транспортным потоком можно управлять с помощью изменения параметров движения, изменения направления движения. Это возможно делать с помощью управляемых дорожных знаков на базе световодов или светодиодов. К критериям, с помощью которых можно определять эффективность той или иной организации движения, можно отнести задержки, длину очереди, время проезда, количество вынужденных остановок.

Структура базы данных для моделирования движения на кольцевом пересечении

В работе [5] изучены критерии эффективности различных схем организации движения на саморегулирующихся кольцевых пересечениях. Рассматривались четырехлучевые кольцевые пересечения с диаметром центрального направляющего островка от 30 до 80 метров. Для них определены границы применения одного из четырех (см.выше) вариантов организации движения. В качестве критериев выбраны средняя задержка и длина очереди. Методика выбора представлена в работе [5, с. 111–112]. Кольцевое пересечение рассматривается как совокупность четырех въездов на кольцо, то есть как комплекс четырех Т-образных примыканий. На каждом въезде определяется вариант организации движения: приоритет кольцевому потоку или приоритет въезжающему потоку.

Информация о состоянии транспортных потоков на улично-дорожной сети, необходимая для расчетов в рамках модели TIMeR_Mod, содержится в матрицах ASTREETS и BINTERSECTION. Ранее авторами описаны методы сбора с помощью видеорегистраторов необходимой для данных матриц информации и ее обновления в динамическом режиме [7]. С целью обновления информации о состоянии транспортных потоков и его прогнозирования на следующий краткосрочный период времени применяется фильтрация Кальмана. На каждом этапе прогнозируемые данные корректируются с помощью данных, полученных путем непосредственных измерений. В результате по имеющейся информации о состоянии транспортных потоков на кольцевом пересечении для определения наиболеее эффективного в текущий момент способа организации движения предлагается действовать по следующему алгоритму:

– по формулам (1) и (2) определить среднюю задержку и длину очереди в выбранном узле;

– по алгоритму [5, с. 111–112] определить организацию движения на данном въезде на кольцо;

– отобразить необходимую информацию в базах данных ASTREETS и BINTERSECTION;

– отобразить необходимую информацию на управляемых дорожных знаках.

Заключение

В условиях ИТС возможна гибкая система управления движением на саморегулирующихся кольцевых пересечениях. Имея информацию, поступающую с видеорегистраторов и отраженную в матрицах ASTREETS и BINTERSECTION, возможно в динамическом режиме управлять движением, выбирая наиболеее оптимальный вариант. Управление в режиме on-line позволяет реагировать на текущую обстановку в транспортной сети и выбирать наиболее эффективный способ организации движения.

Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект № 16-48-230720 р_а.

Библиографическая ссылка