Для расчета адсорбции второго компонента бинарной системы А-В, где А и В компоненты системы следует использовать выражение [6]
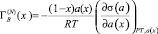 , (1)
, (1)
где a(x) – термодинамическая активность второго компонента системы А-В, σ(a) – функция изотермы поверхностного натяжения (ПН), x – термодинамическая концентрация второго компонента. Однако из-за сложности аналитического определения функций a(x), при условии 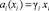 , где i = A и B, γi – коэффициент активности от (1), переходят к выражению
, где i = A и B, γi – коэффициент активности от (1), переходят к выражению
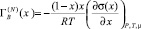 . (2)
. (2)
В (2) изотерму ПН или σ(х) – определяют в эксперименте, а величину 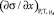 находят способом графического дифференцирования экспериментальной кривой σ(х), что допускает ошибки до 13 и более процентов [1]. Для уменьшения ошибок в расчетах в [7] было предложено уравнение изотермы ПН
находят способом графического дифференцирования экспериментальной кривой σ(х), что допускает ошибки до 13 и более процентов [1]. Для уменьшения ошибок в расчетах в [7] было предложено уравнение изотермы ПН
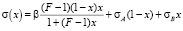 . (3)
. (3)
Здесь β и F – параметры, независящие от состава раствора, σА и σВ – ПН чистых компонентов системы А-В.
В [2] показано, что (3) описывает эксперимент с высокой точностью и предложена методика определения β и F из данных эксперимента по изучению изотерм ПН (см. ниже). В [7] было показано, как использовать (3) при вычислении 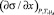 для расчета адсорбции компонентов раствора.
для расчета адсорбции компонентов раствора.
Оценка величины адсорбции компонентов в приближении идеальных растворов
Продифференцировав (3) по х и подставляя полученное выражение в (2), было получено [7] выражение для расчета адсорбции второго компонента.
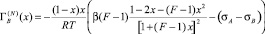 . (4)
. (4)
Формула (4) значительно уменьшает ошибки, допускаемые при графическом дифференцировании экспериментальной кривой σ(x), однако она позволяет вычислить адсорбцию в приближении идеального раствора (γi = 1).
Расчет адсорбции компонентов в приближении реальных растворов
Чтобы приблизиться к данным для реальных растворов, в [3] было предложено вычислить адсорбцию второго компонента бинарной системы А-В с использованием определения адсорбции в N – варианте Гуггенгейма – Адама [1]
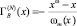 , (5)
, (5)
где
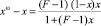 ; (6)
; (6)
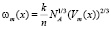 . (7)
. (7)
В (7) 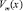 – молярный объем раствора состава х, который определим как
– молярный объем раствора состава х, который определим как
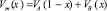 , (8)
, (8)
где VA и VВ – молярные объемы компонентов А и В. Результаты вычислений по (7) будут точнее при использовании экспериментальных 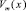 . Нами расчеты были проведены в приближении жесткого раствора (k и n = 1).
. Нами расчеты были проведены в приближении жесткого раствора (k и n = 1).
Для определения параметров β и F уравнения (3) перепишем в виде [4]
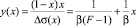 , (9)
, (9)
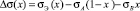 , (10)
, (10)
sэ(х) – ПН расплава состава х, определенное в эксперименте. Очевидно, что из данных эксперимента можем вычислить величину 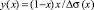 . Тогда, построив график функции y(х), будем иметь прямую (9), наклоненную к оси х под углом a. Продолжив прямую до пересечения с осью OY, определим отрезок, равный
. Тогда, построив график функции y(х), будем иметь прямую (9), наклоненную к оси х под углом a. Продолжив прямую до пересечения с осью OY, определим отрезок, равный
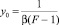 . (11)
. (11)
Угол наклона прямой (9) к оси OX определяет величину b:
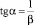 . (12)
. (12)
Решив совместно (11) и (12), найдем значения F и b для данной системы.
Очевидно, что если эксперимент по изучению изотермы ПН дает прямую линию, то уравнение (3) для данной системы справедливо и может быть использовано для расчетов адсорбции компонентов в приближении идеальных растворов по (4) и для расчетов адсорбции компонентов в приближении реальных растворов по (5)–(8).
Действительно, расчет адсорбции висмута в хорошо изученной системе Pb-Bi по формулам (1), (4) и (5)–(8) показал [5] хорошее совпадение данных, полученных по (1) и (5)–(8) (см. рис. 1).
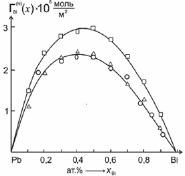
Рис. 1. Результаты расчетов адсорбции висмута в расплавах системы Pb-Bi при Т = 673 К:  – в приближении идеального раствора по (2); о – с учетом термодинамической активности по (1); Δ – по формуле (4)
– в приближении идеального раствора по (2); о – с учетом термодинамической активности по (1); Δ – по формуле (4)
Как видно из сравнения результатов (рис. 1), расчет адсорбции по (5)–(8) дает данные более близкие к реальным растворам. Итак, этот способ может быть использован для расчетов адсорбций компонентов расплавов бинарных систем в случае монотонного изменения ПН в зависимости от состава. Представляет определенный интерес применить этот метод к системам, в которых компоненты образуют устойчивые химические соединения типа AmBn. Ниже рассмотрим эту задачу для систем Ag-Te и Sb-Se, в которых компоненты образуют интерметаллические соединения Ag2Te и Sb2Se3 [4, 8].
Изотермы ПН бинарных систем Ag-Te и Sb-Se
На рис. 2 и 3 представлены экспериментальные изотермы ПН бинарных систем Ag-Te и Sb-Se, построенные в [4] и [8]. Точки – при температурах Т = 1473 К и 923 К соответственно. Здесь же приведены теоретические изотермы ПН (сплошные линии), построенные по уравнению (3).
Как видно из рис. 2 и 3, уравнение (3) описывает экспериментальные изотермы ПН вполне удовлетворительно.
В [9] показано, что при вычислениях адсорбции компонентов системы А-В, в которых компоненты образуют химические соединения АmBn, необходимо переходить к приведенным концентрациям:
для А-Аm Bn
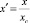 ; (8)
; (8)
и для Аm Bn-В
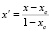 . (9)
. (9)
Здесь хс – концентрация, определяющая состав химсоединения АmBn.
После расчетов адсорбции компонентов в системе x’ результаты следует обратно переводить в систему нормальных концентраций х второго компонента В по формулам (8) и (9).
Таблица 1
Граничные значения ПН и результаты вычислений β и F
|
№ п/п |
Система |
Вторичная система |
sA мН/м |
sB мН/м |
b мН/м |
F |
|
1 |
Ag-Te |
Ag-Ag2Te |
880 |
340 |
– 50 |
21 |
|
Ag2Te-Te |
340 |
150 |
– 243 |
1,95 |
||
|
2 |
Sb-Se |
Sb- Sb2Se3 |
380 |
155 |
– 417 |
1,6 |
|
Sb2Se3-Se |
155 |
50 |
– 250 |
1,36 |
Таблица 2
Входные данные для расчетов 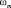 для систем Ag-Te и Sb-Se
для систем Ag-Te и Sb-Se
|
Система |
МA•103, кг/моль |
МB•103, кг/моль |
ρA, кг/м3 |
ρB, кг/м3 |
ωA•10-4 м2/моль |
ωB•10-4 м2/моль |
|
Ag-Te |
102,87 |
127,6 |
10500 |
6240 |
3,99 |
6,30 |
|
Sb-Se |
121,75 |
78,96 |
6690 |
4800 |
5,88 |
5,40 |
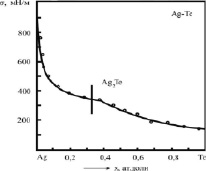
Рис. 2. Изотерма ПН бинарной системы Ag-Te: °- – эксперимент [4]; – – расчет по (3)
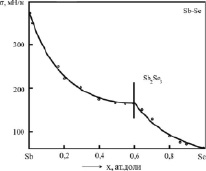
Рис. 3. Изотерма ПН бинарной системы Sb-Se: °- – эксперимент [8]; – – расчет по (3)
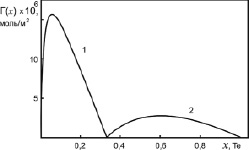
Рис. 4. Адсорбция компонентов бинарной системы Ag-Te: 1 – адсорбция молекул Ag2Te; 2 – адсорбция атомов Te
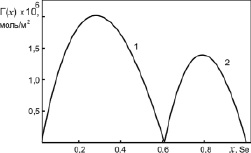
Рис. 5. Адсорбция компонентов бинарной системы Sb-Se: 1 – адсорбция молекул Sb2Se3; 2 – адсорбция атомов Se
Результаты экспериментов [4] и [8] нами обработаны по методике [2], построены теоретические изотермы по (3) (сплошные линии на рис. 2 и 3) и найдены параметры b и F уравнения (3) для каждой вторичной системы Ag-Ag2Te и Ag2Te-Te; Sb-Sb2Se3 и Sb2Se3-Se (cм. табл. 1).
В табл. 2 приведены входные данные для расчетов мольных поверхностей чистых компонентов серебра, теллура, сурьмы и селена.
Результаты расчетов адсорбций компонентов систем Ag-Te и Sb-Se
Результаты наших расчетов адсорбций молекул Ag2Te, Sb2Se и чистых металлов в расплавах бинарных систем Ag-Te и Sb-Se представлены на рис. 4 и 5.
Как видно из рис. 3 и 4, молекулы химсоединений Ag2Te и Sb2Se3 проявляют поверхностную активность в областях 0 < х < 0,33 и 0 < х < 0,6, соответственно. При этом молекулы Ag2Te являются более поверхностно активными, чем Sb2Se3 по отношению к серебру и сурьме. В областях 0,33 < х < 1 и 0,6 < х < 1 на поверхностях расплавленных химсоединений Ag2Te и Sb2Se выходят атомы чистых компонентов Te и Se, а молекулы Ag2Te и Sb2Se3 проявляют поверхностную инактивность по отношению к атомам Te и Se.
Выводы
1. Для расчетов адсорбций компонентов бинарного расплава системы A-B, компоненты которой образуют устойчивые химические соединения AmBn, при температурах измерений поверхностного натяжения бинарную систему A-B необходимо разделить на составляющие вторичные A-AmBn, AmBn-B и расчеты проводить для каждой вторичной системы в приведенной системе концентрации с последующим перерасчетом результатов в нормальную систему концентрации.
2. На примерах бинарных систем Ag-Te и Sb-Se показано, что молекулы Ag2Te и Sb2Se3 могут значительно повлиять на ход изотерм адсорбции Te и Se.
3. Оказалось, что молекулы Ag2Te и Sb2Se3 ведут себя как поверхностно активные по отношению к серебру и сурьме в областях 0 < х < 0,33 и 0 < х < 0,6, и поверхностноинактивные по отношению к Te и Se при х > 0,33 и х > 0,6.
Библиографическая ссылка
Шериева Э.Х., Реуцкая Н.С., Калажоков З.Х., Калажоков Х.Х. АДСОРБЦИЯ КОМПОНЕНТОВ РАСПЛАВОВ БИНАРНЫХ СИСТЕМ AG-TE И SB-SE // Фундаментальные исследования. 2016. № 12-1. С. 107-111;URL: https://fundamental-research.ru/ru/article/view?id=41055 (дата обращения: 10.03.2026).



