Процесс вулканизации относится к классу сложных химико-технологических процессов и протекает в условиях постоянно действующих возмущений стохастической природы, которые являются источниками или факторами неопределенности и существенно влияют на ход технологического процесса вулканизации.
В связи с тем, что, как это отмечалось в работе [3], оптимальная стратегия интенсификации процесса вулканизации не инвариантна вариациям возмущающих воздействий, для обеспечения заданного качества вулканизации необходимо учитывать факторы неопределенности. Задача интенсификации данного процесса заключается в повышении качества восстановительного ремонта при минимуме энергетических затрат и определяется температурным режимом его проведения. Использование стохастической модели процесса вулканизации приводит к необходимости постановки и решения задач интенсификации на основе теории оптимального управления случайными процессами.
Проблема синтеза в стохастической системе состоит в определении алгоритма или закона управления объектом, обеспечивающего оптимальное протекание процесса или получение наилучшего конечного результата в заданных условиях с учетом случайных полезных сигналов (воздействий) и помех. Формулировка и решение этих стохастических задач осуществляется с применением вероятностных критериев, которые, в отличие от детерминированных, содержат дополнительную операцию статистического осреднения и поэтому являются более сложными.
Во многих задачах управления в условиях неполной информации, связанных с повторяющимися ситуациями, нет необходимости в том, чтобы ограничения удовлетворялись при каждой реализации случая. Затраты на накопление информации или другие затраты, обеспечивающие исключение невязок в условии задачи, могут превышать достигаемый при этом эффект. Часто конкретное содержание задачи требует лишь, чтобы вероятность попадания решения в допустимую область превышала заданное число α > 0. В тех случаях, когда возможные невязки в отдельных ограничениях вызывают различный ущерб, имеет смысл дифференцированно подходить к разным условиям. Чтобы уравновесить ущерб, определяемый невязками в разных условиях задачи, следует ограничить снизу вероятность выполнения каждого из них различными числами α > 0. Обычно α1 > 1/2. Подобные постановки задач стохастического программирования называют моделями с вероятностными ограничениями.
Таким образом, задача интенсификации процесса термообработки эластомерных обкладок заключается в следующем: необходимо определить такие законы изменения токов нагревательных элементов плит, при которых достигается минимум математического ожидания суммы квадратов отклонений, рассчитанной по математической модели и экспериментально определенной температур в «характерных» точках нагревательных плит при ограничениях на мощность и конструктивные параметры нагревательных элементов.
Результаты оценки адекватности полученной модели [2, 4] доказали ее пригодность в целях моделирования и интенсификации процесса термообработки при ремонте эластомерных обкладок гуммированных аппаратов. В результате получим
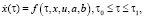(1)
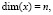
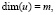
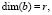
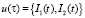– вектор управляющих воздействий;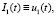 
.
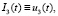
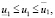
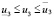С соответствующими начальными условиями:
.
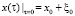Критерий оптимальности имеет вид
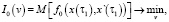
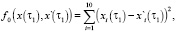
(2)
где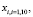 
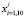– соответственно расчетная и измеряемая в «характерных» точках температура, при условиях связи, представленных в виде уравнения теплопроводности при конкретных граничных условиях и ограничениях на конструктивные параметры и управляющие воздействия
,
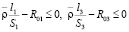и на мощность нагревателя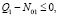 
.
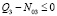Для решения задачи воспользуемся методами оптимизации систем со случайными параметрами [1, 5]. При этом задача (1–2) может быть формализована следующим образом:
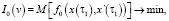
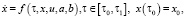
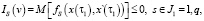
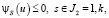
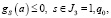(3)
где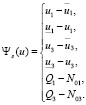 
, 
, 
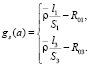
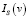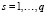представляет собой часть компонентов вектора фазовых координат, не используемых в (2). Определим необходимые условия оптимальности для рассматриваемой задачи, используя методы математической теории экстремальных задач [1].
Вариации δv, где v = {u,а}, в точке v будем называть возможными, если достаточно малое перемещение из точки v∈Θ в направлении вариаций не выводит за пределы множества Θ, т.е. существует такое малое положительное e > 0, (v + εδv)∈Θ.
Функционал (3) является выпуклым и ограниченным, что следует из [3] и для того, чтобы он достигал минимума на Θ в точке v* = {u*,a*}, необходимо и достаточно, чтобы в этой точке не было подходящих вариаций [1].
Решение задачи начинается с определения некоторого исходного un(τ), an, pn, n = 0, 1, 2,...; где n – номер текущей итерации, р = (х0, b).
В нашем случае исходным приближением может служить построенное при решении детерминированной задачи, являющееся аналогом исходной в предположении, что случайные возмущения, записываются математическими ожиданиями u0.
Задача Коши для уравнения (1) решается с заданным приближением un, an. Определяется исходное приближение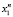 
и вычисляются значения функционалов М[
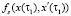] и функций ψs(u), 
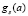при каждом фиксированном τ∈[τ0, τ1].
Далее формируется множество индексов
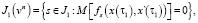
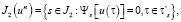
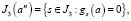(4)
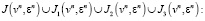
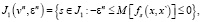
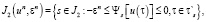
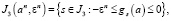
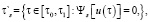
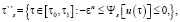(5)
где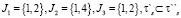 
, множества 
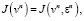совпадают при en = 0, если 
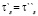, где e – параметры, вводимые для обеспечения сходимости итерационного алгоритма.
Согласно методу возможных направлений [3, 4], введем искусственную переменную s, вектор с положительными компонентами q, и определим конус возможных вариаций:
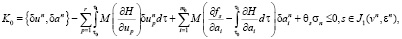
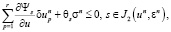
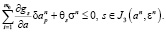(6)
Выберем из всех допустимых вариаций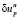 
, 
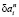удовлетворяющих (6) вариации, имеющие наибольшую скорость убывания функционала (2). Вводя нормализацию 
, 
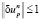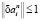||, приходим к необходимости решения задачи вида
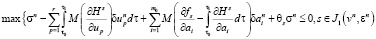
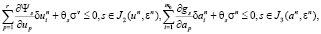(7)
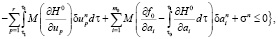
где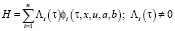 
– непрерывные случайные функции, определенные следующим образом:
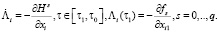
Произвольный вектор (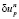
, 
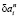, σn), удовлетворяющий (7), при σ ≥ 0 определяет возможные подходящие вариации, так как
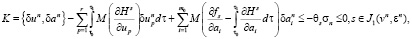
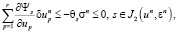
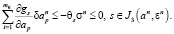(8)
– есть конус возможных вариаций [ ],
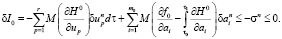
Следовательно, за счет максимизации sn выбираются такие подходящие вариации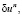 
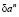в направлении которых функционал (2) убывает, а функция М[Н(t, х, u, а, b, L)] переменного u почти для всех τ∈[τ0, τ1] возрастает достаточно быстро. Основное значение нормализации – это обеспечение единственности решения вспомогательной задачи выбора подходящих вариаций. В направлении наискорейшего спуска 
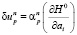задача о выборе возможных вариаций (7) сводится к отысканию конечномерного вектора (an, dan), обеспечивающего
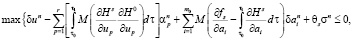
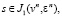
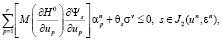
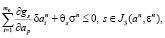(9)
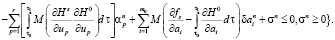
Здесь коэффициенты при неизвестных apn – известные величины, вычисляемые при un, an, pn вдоль n-х траекторий по формулам
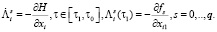(10)
Случайные величины и вектор-функции, входящие в правые части (9), (10), моделируются по их заданным вероятностным характеристикам. Наиболее простую вычислительную схему имеют алгоритмы, построенные на основе метода Монте-Карло (статистических испытаний). Для каждой выборки значений реализаций случайных векторов и вектор-функций при помощи численных методов интегрируется система (10), причем численное интегрирование проводится многократно [3]. В результате получается некоторое количество решений (10) для различных значений реализаций векторов и вектор-функций.
Задача выбора подходящих вариаций (9) является задачей линейного программирования с двухсторонними ограничениями на переменные. При ее решении возникают затруднения, связанные с тем, что задача линейного программирования (8) имеет бесконечное число ограничений. Поэтому, как известно [1, 4], для того, чтобы преодолеть эту трудность, интервал времени [t0, t1] покрывается счетной сеткой с шагом t, (узлы сетки tv = nt(n = 0,.., t1 = (Nt)] и улучшение управляющей функции производится при каждом фиксированном τv∈τ0,τ1]. Таким образом, решение (9) сводится к приближенному.
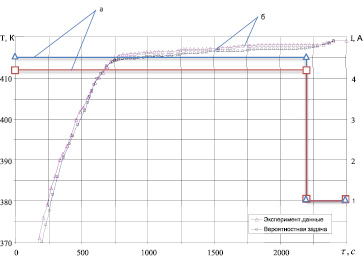
Кинетические кривые теплового режима прогрева покрытия марки 1751 (1,5) + 2566 (1,5 + 1,5 + 1,5) при δст = 4 мм до и по результатам решения вероятностной задачи
Величина шага hn, на который следует сместиться в направлении подходящих вариаций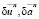 
, вычисляется как наименьший, положительный корень уравнений
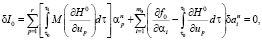(11)
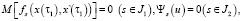
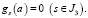(12)
Частные производные и функции вычисляются в точке (un(t) + hn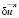
(τ)| τ∈τ’’, an + hn
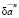); hn – единственная переменная; un(t),an, 
, 
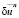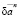– известные векторы; τ» = ∪sτs. Если какое-либо из уравнений (12) не имеет положительных корней, то его наименьший положительный корень полагается равным ∞.
Определим ΔI0 = I0(u n+1) – I0(un). Поскольку решение задачи имеет в большинстве случаев быструю сходимость по функционалу и несколько медленнее сходится по управлению, то находится также ΔН = M[H(u n+1) – H(un)] для каждого [τ0, τ1]. Производим оценку ΔI0, ΔН. Если |ΔI0| < ε0, |ΔН| < ε0, J(vn, εn) = J(vn), после этого итерационный процесс прекращается. В противном случае переходим к определению un(τ), an, pn и продолжаем вычисления используя новое приближение
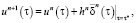
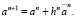
Таким образом, метод возможных направлений предусматривает выбор начального приближения, выбор подходящих вариаций, в направлении которых функционал I0(v) убывает, а функция М[Н] переменного u почти для всех τ∈[τ0, τ1] возрастает достаточно быстро, обеспечение условий сходимости процесса к оптимальному решению, определение длины шага и оценку приближений.
Результаты решения задач интенсификации для различных марок ремонтируемых гуммировочных покрытий [3, 4] представлены на рисунке, где под буквой «а» показаны законы изменения токов нагревательных элементов плит, под буквой «б» – изменение во времени средней по поверхности температуры вулканизируемого участка ремонтируемого покрытия. Кривая 1 описывает изменения средней по поверхности температуры при эксперименте по результатам реализации детерминированной задачи процесса вулканизации, кривая 2 характеризует изменение температуры, полученное при реализации решения вероятностной задачи.
На рисунке «а» представлено управляющее воздействие процессом вулканизации при ремонте покрытия марки 1751 (1,5) + 2566 (1,5 + 1,5 + 1,5) при δст = 4 мм, которое представляет собой кусочно-постоянную функцию. График имеет две ярко выраженные площадки (основной нагрев и остывание в индукторе), что не противоречит физико-химическим основам процесса вулканизации. Первая площадка, находящаяся на уровне 4,2 А, имеет продолжительность 2400 с и соответствует процессу разогрева, вторая – соответствует процессу выдержки.
При сравнении результатов можно сделать обоснованный вывод, что введение в математическую модель формализованных возмущений стохастической природы позволяет существенно снижать максимальные значения токов (до 5–7 %) и, как следствие, обеспечивать меньшие затраты электроэнергии.
Характерной особенностью найденных законов является разная высота площадок по отношению к найденным законам процесса ремонта покрытий, что объясняется толщиной нагреваемых участков ремонтируемых покрытий.
Библиографическая ссылка
Осипов Ю.Р., Демакова А.О., Шилова А.О., Ночевалова Ю.А., Осипов С.Ю., Богданов Д.А. ЗАДАЧА ИНТЕНСИФИКАЦИИ ТЕПЛООБМЕНА ПРИ ВОССТАНОВЛЕНИИ ЭЛАСТОМЕРНЫХ ПОКРЫТИЙ НА ОСНОВЕ ТЕОРИИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ // Фундаментальные исследования. – 2016. – № 12-1. – С. 96-101;URL: https://fundamental-research.ru/ru/article/view?id=41053 (дата обращения: 09.10.2024).