Регуляторы, передаточная функция которых образована тремя слагаемыми, пропорциональным, дифференцирующим и интегральным звеньями, выходные сигналы которых суммируются, относятся к наиболее распространенному типу регуляторов. Широкое распространение регуляторов этого типа определяется простотой построения и промышленного использования, низкой стоимостью, робастностью в различных условиях работы, а также пригодностью для решения большинства практических задач. Наибольшую эффективность ПИД-регуляторы показывают при управлении объектами, которые могут быть представлены моделями второго порядка [3]. Несмотря на достигнутые результаты в области теории конструирования ПИД-регуляторов и накопленный опыт их практического применения, в выборе параметров настройки зачастую продолжают использоваться эмпирические методы. Главной проблемой при настройке коэффициентов ПИД-регулятора является сложность установления соответствия между показателями качества и робастности системы и коэффициентов регулятора [5].
Долгое время настройка параметров регулятора осуществлялась эвристическим ручным методом, основанным на интуиции. В 1942 г. американские учёные J. Ziegler и N. Nichols при исследовании систем с ПИД-регуляторами установили следующие закономерности:
– оптимальная зона пропорциональности пропорционального регулятора в два раза меньше величины зоны пропорциональности, при которой в САУ начинается автоколебательный процесс;
– время изодрома Tи и время предварения Tд зависят от периода возникающих автоколебаний [1].
Методы Зиглера – Никольса являются приближенными и относятся к числу наиболее ранних методов настройки ПИД-регуляторов. Их особенностью является нахождение параметров регулятора по эмпирическим формулам. В качестве критерия оптимальности в данных методах была принята величина декремента затухания D = 0,2 – 0,3. Декремент затухания D выражается через отношение двух амплитуд выходной величины, отстоящих друг от друга на половину периода:

Зиглер и Никольс предложили два метода настройки ПИД-регулятора: первый основан на параметрах переходной характеристики, второй на частотных характеристиках объекта управления [2]. Оба метода обладают невысокой точностью, но дают надежные результаты и применяются при настройке параметров регуляторов. В последнее время методика Зиглера – Никольса снова приобрела популярность, поскольку может быть использована автоматических системах настройки параметров регуляторов.
Рассмотрим параметрический синтез ПИД-регулятора по временному модифицированному методу Зиглера – Никольса.
Несмотря на разнообразие и сложность реальных объектов в системах управления с транспортной задержкой на практике, как правило, используются модели не выше второго порядка. В качестве объекта управления выберем объект второго порядка с передаточной функцией
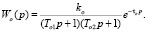
Такая передаточная функция характерна для многих производственных процессов. Задача состоит в нахождении коэффициентов ПИД-регулятора по параметрам переходной характеристики объекта.
Рассмотрим алгоритм модифицированного метода Зиглера – Никольса.
1. Определяем переходную характеристику объекта и её производную, используя модель объекта в Simulink, представленную на рис. 1. В состав модели входят модуль формирования производной переходной характеристики, интегратор с передаточным коэффициентом, равным величине экстремума импульсной переходной характеристики и модуль сдвига переходной характеристики идеального интегрирующего звена так, обеспечивающий ее прохождение через точку перегиба переходной характеристики объекта.
2. По максимальному значению производной выходного сигнала находим точку перегиба переходной характеристики и строим касательную к переходной характеристике в данной точке. Касательная к переходной характеристике будет являться аппроксимирующей прямой для данной характеристики. Тангенс угла наклона аппроксимирующей прямой K = max[dh(t)/dt], смещение аппроксимирующей прямой относительно начала координат задается изменением параметра a с помощью модели в Simulink.
3. Определяем численные значения параметров a (смещение по оси ординат) и L (смещение по оси абсцисс) по графику переходной характеристики и касательной к ней в точке перегиба.
4. Определяем параметры ПИД-регулятора по формулам таблицы.
Уравнение ПИД-регулятора представлено в виде
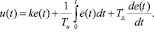
5. Строим модель системы с ПИД-регулятором в Simulink и проводим исследование характеристик системы.
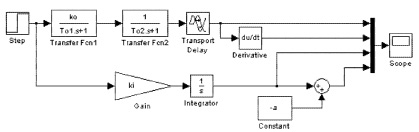
Рис. 1. Модель для исследования разомкнутой системы и расчета параметров Зиглера – Никольса
Формулы для расчёта параметров ПИД-регулятора по временному методу Зиглера – Никольса
|
Параметры регулятора |
|||
|
Вид регулятора |
K |
Tи |
Tд |
|
П |
1/a |
||
|
ПИ |
0,9/a |
3L/k |
|
|
ПИД |
1,2a |
2L/k |
0,5Lk |
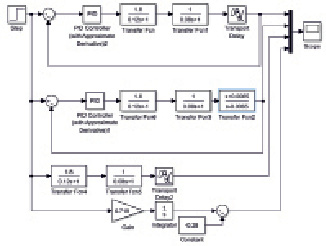
Рис. 2. Модель для исследования системы управления
Метод Зиглера – Никольса позволяет получить надежные, но далекие от оптимальных настройки регулятора.
Качество оценки параметров регулятора можно повысить за счет использования современных средств моделирования и применения специальных инструментариев вычислительных сред. В среде MatLab для настройки параметров регуляторов разработан инструмент PID Tuner приложения System Control Designer. Данный инструмент не предназначен для работы с неминимально фазовыми звеньями, каковым является звено транспортной задержки.
Для решения данной проблемы воспользуемся аппроксимацией Паде. Аппроксимация Паде является методом аппроксимации аналитических функций и заключается в представлении функции в виде отношения двух полиномов, коэффициенты которых определяются коэффициентами разложения функции в ряд Тейлора. Разложение экспоненциальной функции вида 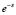 в ряд Тейлора в окрестности точки t = 0:
в ряд Тейлора в окрестности точки t = 0:
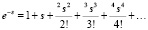
В целях моделирования систем управления обычно достаточно применения аппроксимации Паде низких порядков [4]. Ниже представлены формулы первого и второго порядка для аппроксимации транспортной задержки первого и второго порядка:
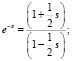
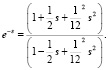
Рассмотрим пример выполнения предложенного алгоритма.
Зададимся передаточной функцией объекта управления в виде
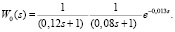
Для настройки параметров ПИД-регулятора в среде MatLab/SIMULINK собрана схема, представленная на рис. 2.
По отклику модели (рис. 3) определяем базовые расчётные параметры:
a = 0,128, h'max = 6,719, L = 0,045 – величина смещения аппроксимирующей прямой по оси абсцисс.
Параметры ПИД-регулятора, рассчитан согласно формулам из таблицы.
K = 4,2257, Tи = 0,021c, Tд = 0,0964, Kи = 47,619 c-1, Kд = 0,1655 c.
Показатели качества системы управления с найденными согласно представленному методу параметрами регулятора составляют: перерегулирование 42 %, время переходного процесса 0,453 с.
Проиллюстрируем возможность использования аппроксимации Паде. На рис. 4 представлены графики переходных процессов в замкнутой одноконтурной системе. Как видно из приведенного графика, использование аппроксимирующей функции второго или даже более высоких порядков не является необходимым.
Перейдем к оптимизации параметров регулятора. Для этой цели воспользуемся инструментами PID Tuner приложения System Control Designer. В данном приложении параметры ПИД-регулятора вычисляются автоматически для установленных показателей качества либо для соответствия выбранной эталонной модели. Требования к качеству управления в PID Tuner задаются численными значениями времени переходного процесса и оценкой робастности во временной области, либо частотой среза и запасом устойчивости по фазе в частотной области. Если считать, что объект управления подвержен значительным изменениям, следует увеличить коэффициент робастности или запас устойчивости по фазе (в зависимости от используемого алгоритма).
Поскольку PID Tuner работает только с линейными системами, заменим в схеме элемент транспортной задержки аппроксимирующей функцией первого порядка.
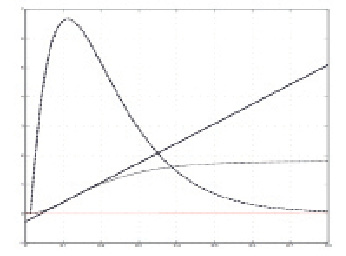
Рис. 3. Импульсная и переходная характеристики объекта управления (пунктирная линия), аппроксимирующая прямая к переходной характеристике (сплошная линия)
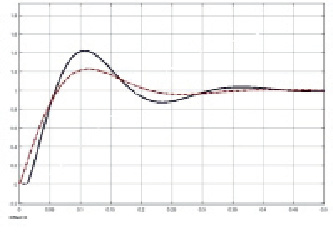
Рис. 4. Переходные характеристики системы с транспортной задержкой (черная сплошная линия), с аппроксимирующим элементом 1 порядка (черная пунктирная линия), аппроксимирующим элементом 2 порядка (красная пунктирная линия)
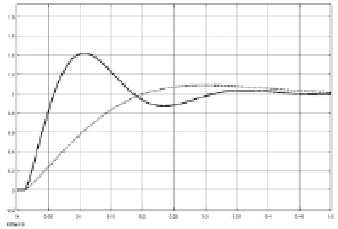
Рис. 5. Графики переходных характеристик САУ с настройками регулятора по методу Зиглера – Никольса (сплошная линия) и оптимизированные по заданным показателям качества в среде МatLab
Зададим требуемые показатели качества системы: время переходного не более 0,4 с и коэффициент робастности равный 0,6. Рассчитанные согласно указанным требованиям параметры регулятора составили: K = 1,022, Kи = 7,178 c-1, Kд = 0,030 c. Показатели качества системы управления с полученными параметрами регулятора составляют: перерегулирование 9 %, время переходного процесса 0,39 с.
На рис. 5 представлены результаты, переходные характеристики системы управления с параметрами регулятора, найденными с использованием модифицированного метода Зиглера – Никольса, а также параметрами, найденными процедурой автоматической подстройки в MatLab.
Аналитические методы определения параметров ПИД-регулятора не позволяют получить оптимальной настройки, поскольку базируются на сильно упрощенных моделях, но их применение является необходимым для получения предварительных настроек, без которых точная настройка может занять недопустимо много времени.
Библиографическая ссылка
Коломыцев В.Г., Рустамханова Г.И. МОДИФИКАЦИЯ ВРЕМЕННОГО МЕТОДА ЗИГЛЕРА – НИКОЛЬСА И ОПТИМИЗАЦИЯ ПАРАМЕТРОВ ПИД-РЕГУЛЯТОРОВ СРЕДСТВАМИ MATLAB // Фундаментальные исследования. 2016. № 11-3. С. 526-531;URL: https://fundamental-research.ru/ru/article/view?id=41010 (дата обращения: 05.01.2026).



