Необходимость применения логистики и логистических моделей в управлении розничными предприятиями уже давно ни у кого не вызывает сомнений и обуславливается непрерывным стремлением любого руководства предприятия увеличить прибыль, снизить усложнением системы рыночных отношений.
Рис. 1. Логистика и связанные с ней области науки
В рамках концепции минимизации издержек перед службами логистики стоит задача снижения затрат на операции хранения и транспортировки. В результате возникает целый комплекс математических задач, решение которых позволяет создать интегрированную логистическую систему розничного предприятия [6].
Рассмотрим бизнес-процесс, связанный с товародвижением в рамках розничного предприятия. В списке ниже представлена последовательность операций над товаром, которая обеспечивает его попадание от поставщика до полки магазина.
1. Формируется заказ на покупку (исходя из предположений о спросе).
2. Товар приходит на склад.
3. Товар принимается и оприходуется на склад.
4. Товар сортируется и помещается в ячейки хранения.
5. Товар поступает в сборку заказа на продажу.
6. Готовый заказ помещается в транспортное средство (ТС).
7. ТС отправляется в рейс.
8. Заказ доставляется покупателю.
Разберем подробно те математические задачи, которые формируются в процессе логистической деятельности розничного предприятия и её последующей оптимизации.
Определение спроса на товар
Современные концепции логистики подразумевают, что вопрос определения величины спроса на товар находится в ведении именно логистических служб предприятия, следовательно, и прогнозирование спроса можно отнести к задачам логистики [8].
Пусть розничная сеть продает n товаров. В распоряжении аналитиков имеются данные об объемах запасов товара i в период времени t –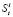 
. Необходимо построить прогноз спроса на следующие 2–6 месяцев. Величина спроса 
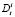на i-ый товар в период времени t естественно отличается от объема запасов 
. 
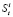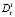можно найти следующим образом [4]:
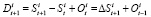, (1)
где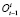 
– объем заказа i-го товара в периоде времени t – 1. Исходя из того, что заказ на доставку товара в периоде t делается в предыдущем периоде – (t – 1)). 
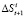представляет собой разность уровней временного ряда, значение которых в общем виде имеет вид
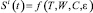, (2)
где T – трендовая компонента, W – сезонная компонента, C – циклическая компонента, ε – случайное отклонение [5]. Однако спрогнозированное значение будет точным при условии неизменности количества точек сбыта. Если учесть в рассматриваемой задаче следующие параметры:
– K – количество точек сбыта в период времени t;
– 
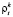– плотность населения в прилегающей к точке сбыта зоне – l метров;
– 
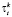– часы работы точки сбыта k в период t;
– и др.,
то получится следующий прогноз спроса для предприятия розничной торговой сети:
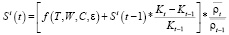, (3)
где Kt и Kt–1 – количество точек сбыта в момент времени t и t – 1.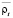 
и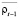 
– средняя плотность населения в обслуживаемых точками продаж областях.
Задача оптимального запаса
Как известно, вместимость склада величина постоянная, а количество хранимых запасов на нем – величина переменная. Разумеется, данное утверждение справедливо с определенной долей условности. Так, например, предполагается, что площадь склада нельзя увеличить, либо это нецелесообразно, либо принимается в виде условности с целью упрощения модели.
Запасы на складе могут теоретически колебаться от 0 до полной загрузки V, однако на предприятиях для каждого склада, как правило, устанавливается «страховой запас» – Kстр.
Очевидно, объем запасов зависит от:
- Потоков груза на склад (OF);
- Потоков грузов со склада (D).
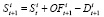, (4)
где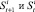 
– объемы запасов товара i на складе в периодах времени t и t + 1. 
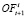– фактическое количество товара i, пришедшее от поставщика в период t + 1. 
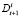– Поток грузов со склада на магазины (принимается равным спросу ввиду наличия страхового запаса) [6].
Фактический объем товара i, приходящего в период времени t –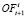 
является величиной стохастической и зависит от объема заказа следующим образом:
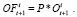(5)
Страховой запас, представленный в формуле 6, должен быть не меньше разности между максимальной величиной спроса и минимальным объемом заказа:
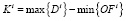, (6)
t – срок хранения грузов на складе
T – время работы склада (сутки / год)
h – оборачиваемость грузов на складе (ед./год)
V – вместимость склада,
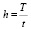. (7)
Задача оптимального размера заказа
Кроме определения вопроса оптимального размера запаса, не менее актуальна задача определения размера заказа и частоты его осуществления. Собственно, перед менеджером по закупкам стоит задача определения этих двух величин.
На этот вопрос можно получить ответ решая задачу поиска экономического размера заказа Economic Order Quantity – EOQ [2]. В традиционной модели общий объем годовых затрат Cr равен
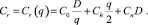(8)
Для максимизации q берется производная
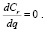(9)
В результате решения получим формулу Харриса – Уилсона.
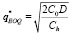(10)
где C0 – накладные расходы на каждую поставку;
D – годовое потребление продукции;
Ch – затраты на хранение единицы продукции в год.
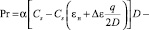
С учетом поправок на неопределенность и процессы естественной убыли 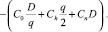[1]:
(11)
При этом оптимальный размер заказа находится по формуле 12 и равен
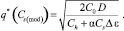(12)
В то же время при условии наличия статистических данных с точки зрения спроса задачу нельзя классифицировать как задачу в условиях неопределенности. И, подставляя прогнозное значение величины спроса в условие задачи, получим следующее выражение для оптимального объема заказа, представленное в формуле:
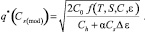(13)
Периодичность заказа при этом исходя из классической задачи определяется остатками товара на складах [3].
Кроме поправок на неопределенность и процессы естественной убыли менеджер, принимающий решение о необходимости формирования нового заказа и его объеме, может учитывать временную ценность денег. Это в свою очередь позволяет принимать во внимание специфику денежных потоков в цепи поставок предприятия и оптимизировать данный сегмент логистической деятельности с учетом обозначенного фактора.
С учетом приведения денежных потоков к одному моменту времени, а также используя формулу начисления простых процентов задача максимизации интенсивности потока доходов приводится к следующему виду:
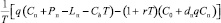(14)
где Cп – стоимость единицы товара (у.е.);
r – годовая процентная ставка, характеризующая преобразование оборотного капитала в прибыль для соответствующей цепи поставок;
dп – дисконтирующий множитель, который равен
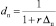. (15)
Рп – прибыль от реализации единицы товара (у.е.);
Т – период времени между поставками, который связан с показателем объема заказа (T = q / D) и является оптимизируемой величиной.
Таким образом оптимальный заказ и оптимальное значение интервала времени для следующего заказа найдется по формулам
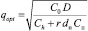(16)
и
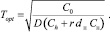(17)
Задача формирования плана перевозок от группы поставщиков группе покупателей
Поставщиками применительно к предприятию розничной торговой сети являются склады предприятия, а потребителями – магазины.
Критерий транспортной задачи:
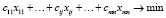, (18)
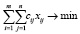, (19)
где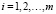 
, а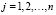 
.
Ограничения
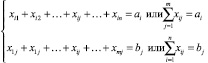. (20)
Кроме того, при решении классической задачи о назначениях накладывается условие, что одну перевозку может совершать одно транспортное средство (применительно к рассматриваемой задаче). Эти условия имеют вид
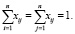
На рис. 2 представлен обзор методов решения задачи маршрутизации или задачи о назначениях [7].
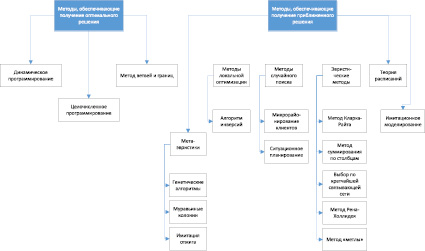
Рис. 2. Методы решения задачи маршрутизации или задачи о назначениях
Классические методы решения задачи оптимизации плана развозки накладывают ограничения, которые не позволяют решать практические задачи. Количество складов, используемых транспортных средств и точек доставки в большинстве случаев не совпадает. Кроме того, не все транспортные средства может понадобиться использовать, равно как и доставка может осуществляться не во все магазины.
Задачу составления оптимального плана доставки следует решать в следующем порядке:
- Задача размещения подготовленных заказов в транспортных средствах. Ограничениями в данной задаче являются тоннажность ТС и их палето-вместимость.
- Задачу закрепления ТС за точками доставки.
Актуальная проблема состоит в том, как решить эти две задачи одновременно с учетом того, что результат одной зависит от решения, другой и наоборот.
Если же данную задачу решить не удастся, то следует прибегнуть к методам, представленным на рис. 2, обеспечивающим приближенные решения.
Библиографическая ссылка
Собко Э.О. ЗАДАЧИ ЛОГИСТИЧЕСКОЙ ЭФФЕКТИВНОСТИ РОЗНИЧНОЙ СЕТИ: МОДЕЛИ И МАТЕМАТИЧЕСКИЕ МЕТОДЫ РЕШЕНИЯ // Фундаментальные исследования. – 2016. – № 11-2. – С. 436-440;URL: https://fundamental-research.ru/ru/article/view?id=40995 (дата обращения: 19.04.2024).