Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Турпак А.М. 1 Ключников А.Т. 1

---

1 ФГБОУ ВО «Пермский национальный исследовательский политехнический университет»

Целью данной работы является разработка методики расчёта и формирование критериев для выбора параметров синус-фильтра – пассивного устройства, состоящего из трёхфазного дросселя и батареи конденсаторов, соединённых треугольником. Новый метод должен позволять варьировать параметры фильтра исходя из текущих потребностей и энергетической эффективности при расчёте. Для расчётов принимается ряд допущений. Исследуется метод выбора параметров синусного фильтра на основе ограничения высокочастотного тока, протекающего через ёмкость, и ограничения падения напряжения на индуктивности. Получены расчётные значения индуктивности Lф?=?12?мГн и ёмкости конденсатора, при соединении звездой Cф?=?6?мкФ. Для исследования коэффициента нелинейных искажений и количественной оценки высокочастотных гармоник при использовании синусного фильтра в среде MATLAB составлена схема математической модели с учётом принятых допущений. Произведено исследование системы при различных параметрах фильтра, модулирующих частотах (fм?=?1, 2, 3?кГц) и различных несущих частотах (fн?=?1,5?Гц). По результатам исследований сделаны выводы относительно выбираемых параметров фильтра.

Статья в формате PDF

0 KB

синус-фильтр

линейный цилиндрический двигатель

математическая модель

коэффициент нелинейных искажений

высокочастотные гармоники

1. Барегамян Г., Маргарян В. Выбор параметров LC-фильтра инвертора с широтно-импульсной модуляцией и синусоидальным выходным напряжением // Силовая электроника. – 2011. – № 29. – С. 50–56.

2. ГОСТ Р 54149–2010. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – М.: Стандартинформ, 2012. – 20 с.

3. Пустоветов М.Ю. Опыт разработки синус-фильтра для силовой схемы частотно регулируемого электропривода // Известия Томского политехнического университета. – 2014. – Вып. 4. – т. 324.

4. Пустоветов М.Ю. Расчёт параметров и компьютерное моделирование синусных фильтров, предназначенных для исключения эффекта озонирования изоляции электродвигателей в частотно регулируемом электроприводе водяных насосных станций // Проблемы трансферта современных технологий в экономику Забайкалья и железнодорожный транспорт: Сборник трудов международной научно-практической конференции. – Чита: ЗабИЖТ, 2011. – С. 8795.

5. Сравнительные исследования энергетических характеристик приводов погружных насосов с асинхронными и вентильными двигателями. Отчет НИР. – М.: РИТЭК-ИТЦ, 2009.

6. Сравнительный анализ электромагнитных процессов в структурах электроприводов нефтедобывающей промышленности / В. Павленко, В. Климов, И. Климов // Силовая электроника. – 2010. – № 26. – С. 30–35.

7. Хабибуллин А.Т. Проявление высших гармоник при работе преобразователей частоты / А.Т. Хабибуллин, Д.О. Хасанов, Р.М. Мухутдинов // Вестник магистратуры. – 2016. – № 1(52). – С. 65–67.

8. Цилиндрический линейный вентильный электродвигатель для погружного бесштангового насоса / А.Т. Ключнков, А.Д. Коротаев, Н.В. Шулаков, С.В. Шутемов // Автоматизация в электроэнергетике и электротехнике. Пермский национальный исследовательский политехнический университет. – 2015. – Т. 1. – С. 158–162.

Электроэнергетика играет ключевую роль как в жизни человека, так и в промышленности. Однако ископаемые источники энергии являются основой для производства электрической (уголь, газ и нефть). Без использования электротехнических устройств их добыча затруднительна. В работе рассматривается составной блок нефтяной промышленности – добыча нефти из скважин, а именно повышение коэффициента полезного действия перспективных погружных установок [5] с линейными двигателями [8] за счёт качественной фильтрации подводимого напряжения.

Цилиндрический линейный вентильный двигатель (ЦЛВД) [8] используется для привода безштангового насоса в погружных установках для добычи нефти из скважин. Специфика использования данного двигателя заключается в длинной кабельной линии (до 3 км) между непосредственно двигателем и преобразователем частоты (ПЧ). При его эксплуатации крайне важно высокое качество фильтрации, так как выходное линейное напряжение ПЧ содержит широкий спектр высокочастотных гармоник. Один из вариантов улучшения качества выходного напряжения – использование фильтра. Общая теория расчёта LC-фильтров излагается в [1, 4, 6]. В данной работе используется методика расчёта синусного фильтра в упрощённом варианте [4], исходя из резонансной частоты LC-контура, которая должна быть не менее чем в два раза меньше модулирующей частоты. Во многих случаях авторы рассматривают работу фильтра без учёта нагрузки.

Разработка методики расчёта синусного фильтра с учётом параметров нагрузки позволит повысить коэффициент полезного действия погружных установок, а также учесть особенности работы потребителей с длиной кабельной линией. Отсюда следует, что разработка методики расчёта LC-фильтра с учётом длинной кабельной линии и нагрузки является актуаль-
ной задачей.

Высокая стоимость фильтра иностранных производителей, отсутствие отечественных аналогов, общий курс на импортозамещение и специфические условия эксплуатации вентильного линейного двигателя – основные причины для создания методики расчёта и выбора параметров индуктивности и ёмкости для погружной установки.

Также были поставлены задачи:

– сформировать критерии выбора параметров элементов синусного фильтра;

– расчётным путём определить характеристики выходного напряжения [7];

– проверить адекватность выбранных параметров с помощью математического моделирования в среде MatLab Simulink;

– исследовать работу фильтра при различных частотах модуляции и несущих частотах.

Расчёт параметров синус-фильтра

Синусный фильтр состоит из трёхфазной индуктивности и ёмкости, соединённой по схеме «треугольник». Особенность этого фильтра заключается в том, что значение его частоты резонанса должно быть меньше половины от значения несущей частоты. В таком случае обеспечивается эффективное сглаживание и подавление высоких частот [7]. Синусный фильтр устраняет импульсные отражения в моторном кабеле, вследствие чего уменьшаются потери и обеспечивается надежная и долговременная работа электродвигателей. В некоторых странах установка синус-фильтров обязательна.

Разработанная модель для исследования влияния параметров синус-фильтра представлена на рис. 1.

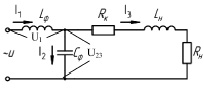
Рис. 1. Расчётная схема цепи:U – выходное напряжение преобразователя частоты; Lф и Сф – ёмкость и индуктивность синус-фильтра; Rк – активное сопротивление кабеля; RН, LН – индуктивное и активное сопротивления нагрузки

Допущения, принятые в данной работе.

1. Использовалась однофазная схема замещения, так как нагрузка и питающий кабель симметричны.

2. Конденсаторы рассчитывались для схемы «звезда» с последующим пересчётом в «треугольник».

3. Индуктивное и ёмкостное сопротивление кабеля не учитывалось.

4. Двигатель представлен статической активно-индуктивной нагрузкой с параметрами, соответствующими началу пуска.

Согласно [3] в качестве индуктивности фильтра возможно использование индуктивности вторичных обмоток разделительных трансформаторов. При отсутствии трансформатора после преобразователя частоты необходимо выбирать индуктивность исходя из падения напряжения ΔU ≤ 5 % (Uном) на индуктивном элементе. Таким образом, индуктивное сопротивление

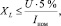(1)

а индуктивность в свою очередь равна

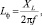(2)

где f – рабочая частота (f = 5 Гц).

Расчётное значение индуктивности в результате Lф = 12 мГн.

Для разработанной схемы замещения получены значения токов и напряжений согласно основным законам электротехники. Расчётные значения представлены на графике (рис. 2).

Минимальное значение ёмкости определяется коридором допустимых значений высокочастотных гармоник тока, которые должны быть не более 10 % от номинального тока [2].

Величина ёмкости С = 6,2 мкФ, на границе коридора (рис. 2 т. А) удовлетворяет условиям критерия. Ёмкости пересчитываются для схемы соединения в треугольник, так как расчёт был для фазного тока в звезде. Таким образом, ёмкость конденсатора для треугольника равна C = 2 мкФ.

Моделирование синус-фильтра

Исследование синусного фильтра отдельно от нагрузки невозможно, так как параметры нагрузки, очевидно, будут влиять на качество выходного напряжения. Исходя из этого, необходимо составить математическую схему, с учётом ЦЛВД и кабеля. Так как величина эдс у непо-
движного ЦЛВД равна нулю, двигатель представлен в виде эквивалентной активно-индуктивной нагрузки.

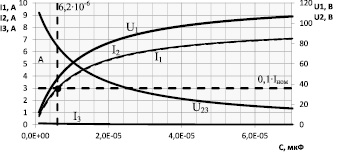
Рис. 2. Графики зависимостей токов и напряжений от величины ёмкости фильтра. U, I = f(С)

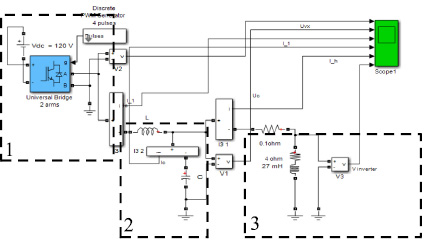
Рис. 3. Структурная схема ПЧ с SIN-фильтром:
1 – ШИМ-инвертор; 2 – синусный фильтр;
3 – статическая нагрузка с параметрами ЦЛВД и с учётом активного сопротивления кабеля

Разработанная математическая модель представлена на рис. 3.

Для исследования рассчитанных параметров фильтра были взяты ещё три комбинации параметров фильтра Lф = 6 мГн; Cф = 12 мкФ; Lф = 2 мГн; Cф = 12 мкФ и Lф = 2 мГн; Cф = 22 мкФ. Для каждого варианта было произведено моделирование системы при различных соотношеничях несущей и модулирующей частот. Результаты занесены в табл. 4 и табл. 5.

Для оценки качества фильтрации исследовался параметр THD с помощью инструмента FFT Analysis в среде MATLAB Simulink. THD – суммарный коэффициент нелинейных искажений (КНИ) периодического сигнала в процентах. THD характеризует, в какой степени сигнал отклонён от синусоидальной формы, даёт количественную оценку нелинейных искажений периодического сигнала.

Полученные результаты КНИ, осциллограмма тока и спектр гармоник при Lф = 12 мГн; Cф = 6 мкФ, fm = 1 кГц; fн = 1 Гц и при Lф = 12 мГн; Cф = 6 мкФ, fm = 1 кГц; fн = 1 Гц представлены на рис. 4.

Расчётные значения КНИ, полученные с помощью инструмента FFT-Analysis, сведены в таблицу. Таблица содержит значения КНИ тока через дроссель, тока через нагрузку и напряжения на нагрузке.

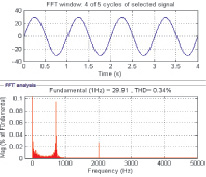
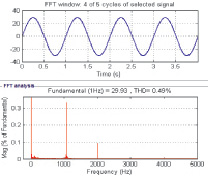
а б

Рис. 4. Осциллограммы токов и напряжений схемы:
а – при Lф = 12 мГн; Cф = 6 мкФ, fm = 1 кГц, fн = 1 Гц;
б – при Lф = 12 мГн; Cф = 6 мкФ, fm = 1 кГц; fн = 1 Гц

Результаты математического моделирования

Заключение

1. Показана методика расчёта параметров индуктивности и ёмкости согласно следующим критериям: величина индуктивности выбрана из условия допустимого на ней падения напряжения в номинальном режиме работы; ёмкость выбрана исходя из условия, что ток высокочастотных гармоник через конденсатор не должен превышать 10 %, то есть Ic ≤ 10 % от Iном.

2. Расчётные параметры фильтра показали необходимость учёта параметров нагрузки в процессе проектирования данного фильтра.

3. Спроектированный синус-фильтр с рассчитанным вариантом Lф = 12 мГн; Cф = 6 мкФ и при частотах fm = 2 кГц; fн = 5 Гц имеет наименьшие значения коэффициента нелинейных искажений тока КI = 2,78 % и напряжения КU = 4,37 % на нагрузке.

4. При изменении параметров фильтра, для Lф = 6 мГн; Cф = 12 мкФ значения искажений на нагрузке практически не меняются (КI = 2,23 % и напряжения КU = 4,45 %).

5. Уменьшение индуктивности, при неизменной ёмкости синус-фильтра влечёт практически пропорциональное увеличение коэффициента нелинейных искажений напряжения.

6. Показана необходимость обязательной установки синусного фильтра при использовании ПЧ с ШИМ.

Библиографическая ссылка