Исследование сложных технических систем, к которым относятся системы холодоснабжения (СХС), практически всегда приходится проводить в условиях отсутствия полной априорной информации об изучаемых системах. Данное обстоятельство обуславливается сложностью их построения и функционирования, неопределенностью влияющих на их работу факторов.
Разработка математического обеспечения контроля и диагностирования СХС сопровождается необходимостью решения этих задач, одной из которых является построение изображений видов технических состояний (ТС) Ei ∈ E, 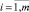 . Под изображением понимается математическое представление вида ТС в виде n-мерного вектора. Координаты eij данного вектора представляют собой типовое (усредненное значение) j-го контролируемого признака (КП) в i-м виде ТС.
. Под изображением понимается математическое представление вида ТС в виде n-мерного вектора. Координаты eij данного вектора представляют собой типовое (усредненное значение) j-го контролируемого признака (КП) в i-м виде ТС.
Проблема решения заключается в том, что нельзя однозначно задать гиперплоскости в многомерном евклидовом пространстве, отделяющие один класс ТС от другого. Это связано с тем, что неизвестны пределы изменения КП
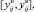
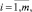
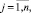 (1)
(1)
соответствующие каждому отказу. Для определения этих пределов необходим значительный объём статистических данных по отказам в процессе эксплуатации, или постановка натурного эксперимента с имитацией отказов, а его постановка в реальных условиях далеко не всегда возможна [2].
В такой ситуации более конструктивным является подход к формированию изображений видов ТС Еi, основанный на использовании информации о фактах выхода значений КП за допустимые пределы.
Изучение значительного числа технических состояний
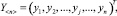 (2)
(2)
соответствующих определённому отказу, позволяет выявить их общие свойства и сформировать изображение данного отказа как вектор числовых характеристик.
Изображения всех отказов представляются как точки в многомерном евклидовом пространстве, на которых и реализуется процесс распознавания наблюдаемых технических состояний Y<n> ∈ Y.
Эта задача может быть решена на основе простого решающего правила
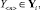 (3)
(3)
если 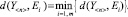
Текущее техническое состояние системы Y<n> идентифицируется с i-м видом его ТС, если расстояние в n-мерном евклидовом пространстве между Y<n> и изображением i-го вида технического состояния Ei является минимальным.
Постановка задачи исследования
Для того чтобы решить задачу построения изображений отказов СХС, необходимы следующие исходные данные:
1) перечень наименований всех видов ТС (отказов) объекта
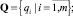
2) состав и пределы изменения КП 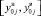 для работоспособного состояния СХС
для работоспособного состояния СХС
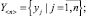 (4)
(4)
3) ограниченная по объёму обучающая выборка реализаций КП, принадлежность которых каждому виду ТС известна:
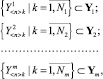 (5)
(5)
где 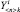 – наблюдаемое состояние, о котором известно, что оно принадлежит i-му виду ТС объекта.
– наблюдаемое состояние, о котором известно, что оно принадлежит i-му виду ТС объекта.
Пределы изменения КП (1), соответствующие всем рассматриваемым отказам, неизвестны и не могут быть определены из имеющейся априорной информации по отказам.
Требуется построить множество изображений
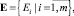 (6)
(6)
наилучшим образом в смысле достоверности распознавания отражающих свойства соответствующих видов ТС и оценить их вероятности.
Решение
В теории распознавания образов разработаны различные алгоритмы обучения на основе методов непараметрической статистики [4, 5, 6]. Все они сводятся к единой математической основе – процедуре итеративного градиентного поиска, при которой на каждом шаге обучения ищется градиент доступной наблюдению случайной функции, математическое ожидание которой подлежит минимизации. Для обоснования данной процедуры в работе [5] применяется метод стохастической аппроксимации.
Суть процедуры итеративного градиентного поиска заключается в следующем. Для каждого класса ТС ищется аппроксимация разделяющей гиперплоскости hi, 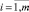 . Поскольку неизвестное пока изображение Ei является опорной точкой i-го вида ТС и может считаться постоянным, hi допустимо трактовать как непрерывную функцию
. Поскольку неизвестное пока изображение Ei является опорной точкой i-го вида ТС и может считаться постоянным, hi допустимо трактовать как непрерывную функцию
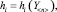 (7)
(7)
где Y<n> – вектор значений КП, являющийся элементом n-мерного евклидова пространства.
В дальнейшем (7) называется разделяющей функцией. Предполагается, что она обеспечивает максимальную точность при распознавании, но является неизвестной. Поэтому следует выбрать класс аппроксимирующих функций, с помощью которых находится наилучшее приближение к разделяющей функции. Эти функции будут обозначаться через 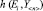 . Мера уклонения аппроксимирующих функций от аппроксимируемой определяется как математическое ожидание случайной выпуклой функции
. Мера уклонения аппроксимирующих функций от аппроксимируемой определяется как математическое ожидание случайной выпуклой функции 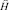 от разности
от разности 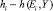 , т.е.
, т.е.
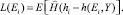 (8)
(8)
Наилучшая аппроксимация соответствует получению такого вектора 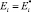 , при котором достигается минимум функционала (8):
, при котором достигается минимум функционала (8):
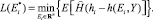
Однако следует иметь в виду, что функционал (8) в явном виде не может быть задан, по причине того, что неизвестна плотность распределения случайной функции 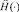 , поэтому неизвестно и её математическое ожидание. Единственная возможность определения искомого вектора
, поэтому неизвестно и её математическое ожидание. Единственная возможность определения искомого вектора 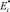 состоит в том, чтобы воспользоваться отдельными реализациями, полученными при «показе» векторов Y из обучающей выборки. В задачах обучения используется разложение аппроксимирующей функции по множеству базисных функций gj(Y),
состоит в том, чтобы воспользоваться отдельными реализациями, полученными при «показе» векторов Y из обучающей выборки. В задачах обучения используется разложение аппроксимирующей функции по множеству базисных функций gj(Y), 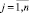 согласно выражению
согласно выражению
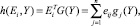 (9)
(9)
где 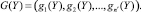
В качестве gj(Y) целесообразно принимать ортогональные или ортонормированные функции. Использование таких функций в теории распознавания образов можно объяснить тем, что их легко воспроизводить и они удовлетворяют условиям теоремы Вейерштрасса о приближении [1], которая утверждает, что любую функцию, непрерывную в замкнутом интервале, можно равномерно аппроксимировать на этом интервале с любой заданной точностью алгебраическим полиномом.
С учётом (9) выражение для функционала (8) принимает вид
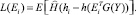 (10)
(10)
Так как функционал (10) в явной форме неизвестен, для поиска минимума L(Ei) используются измеренные градиенты реализаций [5]. Необходимое условие экстремума (10) можно записать в виде уравнения
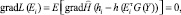 (11)
(11)
где 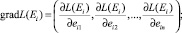
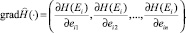
Если функционал L(Ei) выпуклый и имеет единственный экстремум, то условие (11) – необходимое и достаточное для существования данного экстремума. В этом случае корень уравнения (11) даёт оптимальное значение вектора 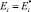 .
.
В работах [5, 6] показано, что если использовать квадратичную меру уклонения аппроксимирующей функции от аппроксимируемой
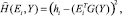
а в качестве вектор-функции Gj(Y) выбрать полную систему ортонормированных функций gj(Y), то минимизация функционала (11) обеспечивается посредством применения в процессе обучения алгоритма Роббинса - Монро. Данный алгоритм применительно к рассматриваемой задаче может быть представлен в виде рекуррентного соотношения [2]:
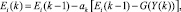 (12)
(12)
где ak – элемент последовательности положительных чисел, удовлетворяющий следующим условиям:
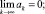
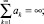
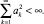
Примером такой последовательности является гармонический ряд
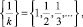 (13)
(13)
который в дальнейшем и будет использоваться в качестве ak.
С учётом (13) рекуррентное соотношение (12) принимает вид
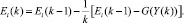 (14)
(14)
Поскольку пределы изменения КП, соответствующие различным отказам, неизвестны, при реализации процедуры обучения следует фиксировать не сами значения 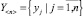 , а факт выхода их за пределы установленных допусков Dj. В этом случае вместо признаков yj можно использовать бинарные значения КП, определяемые из выражения:
, а факт выхода их за пределы установленных допусков Dj. В этом случае вместо признаков yj можно использовать бинарные значения КП, определяемые из выражения:
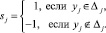 (15)
(15)
В качестве базисных функций gj(Y), которые используются в рекуррентном соотношении (14), реализующем процедуру обучения, могут быть приняты функции [2]
gj(Y) = sjdrj, 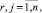 (16)
(16)
где drj – символ Кронекера.
Известно [3], что система таких функций является ортонормированной.
Из (16) следует, что базисные функции определяются как
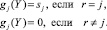
Тогда функция G(Y) представляет собой вектор значений КП в бинарной форме
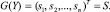 (17)
(17)
Произвольное наблюдаемое состояние Yi, принадлежащее i-му классу, преобразуется аналогично:
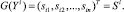 (18)
(18)
Поэтому обучающую выборку, используемую при распознавании отказов, целесообразно представлять в виде
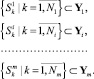 (19)
(19)
Аппроксимирующая функция (9) записывается в форме
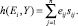 (20)
(20)
Рекуррентное соотношение (14) принимает вид
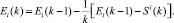 (21)
(21)
Изображения Ei, полученные в соответствии с выражением (21), представляются как векторы нормализованных признаков
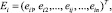 eij ∈ [–1, 1]. (22)
eij ∈ [–1, 1]. (22)
Удобство представления eij в нормализованном виде заключается в том, что каждый из них имеет ясный физический смысл. Положительное значение eij указывает на то, что в обучающей выборке преобладают такие отказы, при которых значения j-го КП не выходят из допуска Dj, и наоборот в случае отрицательного значения.
Например, если eij = –0,5, то это означает, что j-й КП выходит за допустимый интервал (1) в i-м виде технического состояния объекта с вероятностью 0,75.
В ходе исследования для СХС с промежуточным холодоносителем с парокомпрессорной холодильной машиной АИП-900 производились измерения двадцати одного КП. В обзоре представлены данные по четырем КП.
Y<4> = (y1, y2, y3, y4)T,
где y1 – давление хладагента в испарителе; y2 – перегрев хладагента в испарителе; y3 – давление хладагента в конденсаторе; y4 – переохлаждение хладагента в конденсаторе.
Сформирована обучающая выборка вида (19). В качестве i-го вида ТС рассмотрим отказ насоса системы отвода тепла конденсации (в данном исследовании рассматриваются только постепенные отказы, при которых агрегат продолжает работать с недопустимыми параметрами, которые выходят за пределы работоспособного состояния):
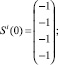
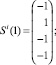
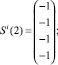
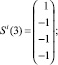
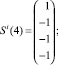
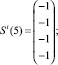
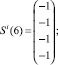
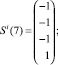
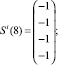
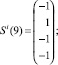
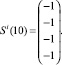
Требуется построить изображение Ei.
Построение изображения Ei осуществляется на основе рекуррентного соотношения (21) и обучающей выборки.
Принимаем Ei(0) = Si(0).

Вероятностная интерпретация значений нормализованных признаков
|
Контролируемый признак |
Значение нормализованного признака eij |
Вероятность выхода i-го КП за допустимый интервал, т.е. yj ∈ Δj, где |
Вероятность нахождения i-го КП в интервале, т.е. yj ∈ Δj, где |
|
у1 |
–0,6 |
0,8 |
0,2 |
|
у2 |
–0,6 |
0,8 |
0,2 |
|
у3 |
–1 |
1 |
0 |
|
у4 |
–0,8 |
0,9 |
0,1 |
Аналогично, используя (21), находим Ei(2), Ei(3), …., Ei(10).
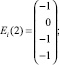
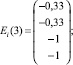
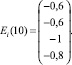
Следовательно, 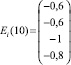 будет являться изображением вида ТС.
будет являться изображением вида ТС.
Вероятностная интерпретация значений нормализованных признаков показана в таблице.
Выводы
Метод стохастической аппроксимации, использованный в исследовании, позволяет построить изображения всех видов ТС СХС при неизвестных пределах измерения КП (1), соответствующих каждому отказу. В представленном примере очевидна простота применения данного метода на практике. Он дает представление о том, как при отказе i-го ФЭ изменяется поведение каждого КП. Таким образом, каждое изображение ТС можно будет различить среди сформированного множества изображений всех видов ТС.
Библиографическая ссылка
Грушковский П.А., Шишкин Е.В., Пудиков В.В. ЗАДАЧА ПОСТРОЕНИЯ ИЗОБРАЖЕНИЙ ВИДОВ ТЕХНИЧЕСКОГО СОСТОЯНИЯ ПО ОГРАНИЧЕННОМУ ОБЪЁМУ НЕОДНОРОДНОЙ АПРИОРНОЙ ИНФОРМАЦИИ В СИСТЕМАХ ХОЛОДОСНАБЖЕНИЯ // Фундаментальные исследования. 2016. № 3-2. С. 245-249;URL: https://fundamental-research.ru/ru/article/view?id=40039 (дата обращения: 03.03.2026).




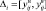 ,
, 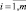 ,
, 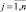
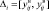 ,
, 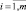 ,
,