В машиностроении широкое распространение получили методы оценки вибрационных и прочностных характеристик конструкций, основанные на математическом моделировании их динамического поведения. Среди них особое место занимают методы модального анализа. В основе модального анализа лежит возможность описания динамического поведения конструкции компактным набором модальных параметров: собственных частот, форм и декрементов колебаний [3, 4]. Знание этих параметров позволяет представить любые колебания линейной системы в виде разложения по собственным формам и тем самым существенно сократить вычислительную трудоемкость моделирования. Однако при определении модальных характеристик моделей, имеющих в своем составе нелинейные элементы, данный метод в классической постановке не дает единственного решения [8] и вынуждает использовать различные методики линеаризации функции поведения контакта. Кроме этого, модальные характеристики зависят от граничных условий, которые в случае реальных конструкций не всегда известны с необходимой точностью [9, 10]. Эти особенности могут усложнить процедуру расчетного определения модальных характеристик конструкции.
Перечисленные трудности в полной мере проявляются при расчете модальных характеристик роторов с неподвижными соединениями элементов, в частности с цанговыми соединениями. Контакт между элементами ротора приводит к нелинейности упругих характеристик. Кроме того, сама поверхность контакта зависит от отклонений от номинала (в пределах допусков на изготовление) реальных размеров сопрягаемых деталей и усилий затяжки резьбовых соединений.
Цель настоящей работы состоит в разработке методики моделирования цанговых соединений деталей при модальном анализе роторов.
Материалы и методы исследования
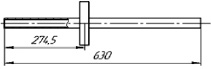
Исследование проводится на примере вала ротора двухвальной модельной роторной установки (рис. 1). Установка предназначена для отработки методик математического моделирования вибрационных процессов, протекающих в роторных системах авиационных газотурбинных двигателей с учетом конструкционных и эксплуатационных факторов [5, 6]. Ротор представляет собой полый вал с закрепленным на нем диском постоянной по радиусу толщины. Масса диска 5,96 кг, его диаметр 200 мм. Наружный диаметр вала 35 мм, внутренний – 30 мм. Диск закреплен на валу ротора с помощью цангового соединения.
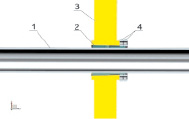
Цанговое соединение (рис. 2) состоит из конической втулки 2, установленной на вал 1, диска 3, установленного на коническую втулку, и двух гаек 4, фиксирующих положение диска на конической втулке 2. Данная конструкция позволяет изменять положение дисков на валу. Втулка 2 – коническая, отверстие диска 3 также коническое. Их размеры выполнены с отклонениями от номинала в пределах заданных допусков. Контакт диска с втулкой осуществляется не по всей конической поверхности, положение и величина зоны контакта зависит от усилия затяжки гайки 4.
Расчетный модальный анализ ротора проводится методом конечных элементов. В расчетной модели сборный ротор выполнен в виде одной твердотельной детали, что исключает необходимость моделирования контактного взаимодействия между деталями и позволяет решать задачу в линейной постановке [2]. Для исключения влияния жесткости закрепления ротора в статоре рассматривались граничные условия «свободный подвес», при которых не накладываются ограничения на перемещения ротора.
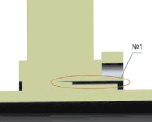
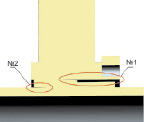
Рассмотрены три варианта моделирования цангового соединения: А – сплошное соединение (рис. 3, а), Б – модель с одним клиновидным разрезом по части конической поверхности между втулкой и диском (рис. 3, б) и модель В – с двумя разрезами (рис. 3, в). Две последние модели позволяют учесть отсутствие полного контакта деталей по всей поверхности конической втулки, а также несовпадение углов раскрытия конической поверхности диска и втулки.

а б
Рис. 1. Внешний вид экспериментальной установки (а) и схема ротора (б)

а б
Рис. 2. Общий вид цангового соединения (а) и узел крепления диска к валу (б): 1 – вал ротора; 2 – коническая втулка; 3 – диск ротора; 4 – гайки

а б в
Рис. 3. Модели цангового соединения: а – без разрезов (А), б – с одним разрезом (Б); в – с двумя разрезами (В)
Расчетные значения собственных частот f расч колебаний ротора и их относительная погрешность ε по сравнению с результатами f эксп экспериментального модального анализа
|
Формы колебаний |
fэксп, Гц |
Модель А |
Модель Б |
Модель В |
|||
|
f расч, Гц |
ε, % |
f расч, Гц |
ε, % |
f расч, Гц |
ε, % |
||
|
1 |
351 |
361 |
2,77 |
352 |
0,28 |
351 |
0 |
|
2 |
580 |
677 |
14,33 |
655 |
11,45 |
630 |
7,94 |
|
3 |
1446 |
1617 |
10,58 |
1500 |
3,6 |
1491 |
3,02 |
|
4 |
2356 |
2462 |
4,31 |
2445 |
3,64 |
2357 |
0,04 |
Анализ результатов расчетного и экспериментального модального анализа
В результате расчетного модального анализа получены собственные формы и частоты колебаний исследуемого ротора для трех описанных выше моделей цангового соединения (рис. 4, таблица).
Для идентификации математической модели был проведен экспериментальный модальный анализ исследуемого ротора методом трехкомпонентной сканирующей лазерной виброметрии с помощью виброметра PSV-400-3D по методике, описанной в [1, 7]. Получены собственные частоты (таблица) и формы колебаний (рис. 4) исследуемого ротора. На рис. 4 видно хорошее согласование первых четырех собственных форм колебаний ротора, полученных экспериментально и расчетным модальным анализом с использованием модели В (рис. 3).
Для моделей Б и В цангового соединения выявлено существенное влияние геометрических характеристик разрезов на результаты модального анализа. В процессе идентификации были определены параметры подрезов, при которых достигались минимальные расхождения между модальными характеристиками, полученными расчетным и экспериментальным методами (рис. 5).
Из таблицы видно, что наибольшую погрешность расчетного моделирования, до 14,33 %, дает модель цангового соединения А, не учитывающая возможность неполного контакта в соединении. Несколько меньшую погрешность, до 11,45 %, обеспечивает модель Б. При использовании модели В, учитывающей возможность неполного контакта деталей с обеих сторон диска, погрешность моделирования может быть снижена до 7,94 %. Наибольшее расхождение в частотах имеет место на 2-й изгибной форме при всех трех вариантах моделирования. При этом расчетная частота во всех случаях получалась выше полученной экспериментально.
Заключение
Разработана методика моделирования цангового соединения при конечно-элементном расчете модальных характеристик роторов. Методика позволяет учитывать анализ в линейной постановке. Для проверки методики проведен расчетный и экспериментальный модальный анализ ротора модельной исследовательской установки. Получены собственные частоты и формы колебаний. Минимальное расхождение между расчетными и экспериментальными значениями собственных частот ротора получено для модели В цангового соединения.


а б

в г


д е

ж з
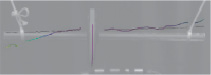
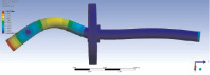
Рис. 4. Собственные формы колебаний ротора, полученные из конечно-элементного расчета (а, в, д, ж) и экспериментального модального анализа (б, г, е, з)
а б
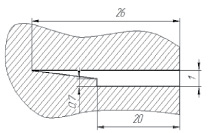
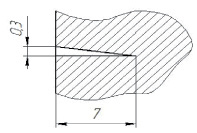
Рис. 5. Размеры клиновидных разрезов в моделях цангового соединения по модели В: а – № 1; б – № 2 (см. рис. 3)
Рассмотренные методики моделирования цангового соединения в линейной постановке могут быть использованы для математического моделирования при отстройке от критических и резонансных режимов роторов, содержащих подобные соединения.
Работа выполнена в рамках реализации государственного задания № 9.576.2014/К Министерства образования и науки России.
Рецензенты:
Бульбович Р.В., д.т.н., профессор, декан аэрокосмического факультета, Пермский национальный исследовательский политехнический университет, г. Пермь;
Колмогоров Г.Л., д.т.н., профессор, заведующий кафедрой «Динамика и прочность машин», Пермский национальный исследовательский политехнический университет, г. Пермь.
Библиографическая ссылка
Нихамкин М.Ш., Мехоношин Г.В., Семенов С.В., Болотов Б.П. ОСОБЕННОСТИ МОДАЛЬНОГО АНАЛИЗА РОТОРОВ С ЦАНГОВЫМИ СОЕДИНЕНИЯМИ ДЕТАЛЕЙ // Фундаментальные исследования. 2015. № 10-2. С. 284-288;URL: https://fundamental-research.ru/ru/article/view?id=39165 (дата обращения: 29.12.2025).



