Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кильдибаева С.Р. 1

---

1 Стерлитамакский филиал ФГБОУ ВПО «Башкирский государственный университет»

В статье рассматривается математическая модель купола-сепаратора, предназначенная для ликвидации разлива нефти при разработке месторождений в шельфе. Тема особенно актуальна в связи с растущим интересом к добыче сырья в шельфе. Установка купола происходит непосредственно над местом утечки углеводородов, в несколько этапов. На первом этапе рассматривается течение углеводородов в затопленной струе и определение теплофизических характеристик, которые используются в качестве начальных параметров для накопления углеводородов в куполе. Далее рассматривается миграция капель нефти и пузырьков газа в куполе. Купол заполнен дизельным топливом (соляркой) для предотвращения накопления гидрата внутри. Накопление гидрата внутри купола важно исключить для его фиксации и стационарной работы. Определены характеристики струи, а также режимы накопления газа и нефти в куполе. Определено изменение температуры струи от вертикальной координаты и её влияние на температуру газовых пузырьков.

Статья в формате PDF

953 KB

купол

разлив нефти в шельфе

затопленная струя

пузырек газа

1. Гималтдинов И.К., Кильдибаева С.Р., Ахмадеева Р.З. Расчет теплофизических и кинетических параметров затопленной струи // Фундаментальные исследования. – 2013. – № 11 (часть 7). – С. 1323–1327.

2. Кильдибаева С.Р. Моделирование течения углеводородов в затопленной струе // Современные проблемы науки и образования. – 2014. – № 6; URL: http://www.science-education.ru/120-15769 (дата обращения: 07.12.2014).

3. Лыков А.В. Теория теплопроводности. – М.: Высш. школа, 1966. – 600 с.

4. Юдаев Б.Н. Теплопередача: учебник для втузов. – М.: Высш. школа, 1973. – 360 с.

5. Lee J.H.W., Chu V.H. Turbulent jets and plumes: a Lagrangian approach. – Kluwer, 2003. – 390 p.

В связи с уменьшением запасов нефти на континенте увеличивается интерес исследователей к разработке месторождений в шельфовой зоне Мирового океана, которые практически нетронуты. Негативной стороной разработки таких месторождений являются неизбежные техногенные аварии, сопровождающиеся выбросами нефти и газа в океан. Последствия таких выбросов загрезняют экосистему региона. Как показал случай разлива в Мексиканском заливе, который произошел в апреле 2010 г., на данный момент отсутствует метод быстрого и качественного устранения утечки такого типа.

Среди предлагаемых методов разлива наиболее привлекательным для инженеров является установка купола непосредственно над местом утечки. При этом такой купол не только способен устранить утечку, но и накапливать внутри нефть и газ для дальнейшей откачки и эксплуатации месторождения в промышленных масштабах.

Пусть на дне океана существует источник углеводородов, из которого с определенным объемным расходом вытекает смесь нефти и газа – метана. Будем полагать, что нефть и газ распространяются в виде затопленой струи, а сама струя представляет собой капли нефти, пузырьки газа и «вовлеченную» в струю окружающую воду. Допустим, что теплофизические параметры струи такие, что пузырьки газа на некоторой высоте превращаются в частицы газового гидрата.

Для сбора нефти и газа под водой на источник углеводородов устанавливается купол, который представляет собой цилиндрическую емкость из полиуретана, снабженную трубками для откачки углеводородов, накапливающихся в куполе (рис. 1).

Как показала практика, помешать фиксации купола над местом утечки нефти и газа может накопление газовых гидратов внутри купола, как это случилось при аварии в Мексиканском заливе. Во избежание проникновения частиц гидрата внутрь купола, на поверхности в него закачивают дизельное топливо (солярку) и герметизируют, после чего опускают к месту утечки углеводородов.

Постановка задачи

Будем полагать, что загерметизированный купол устанавливается над источиком так, чтобы нижнее основание купола находилось на расстоянии 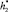от источника углеводородов. В общем случае полагаем, что 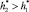. В этом положении нижнее основание купола омывает струя из капель нефти, гидратных частиц и воды, «вовлеченной» в струю. Далее происходит открытие нижнего основания купола специальным механизмом.

Процесс построения математической модели состоит из нескольких этапов. Сначала определим распределение температуры по высоте струи, чтобы знать высоту 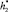, выше которой начинается гидратообразование в струе.

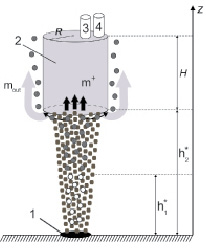
Рис. 1. Схема купола: 1 – источник истечения углеводородов; 2 – купол; 3 – трубка для откачки смеси; 4 – трубка для откачки газа; – высота, на которой открывается нижнее основание купола; – высота, выше которой пузырьки газа покрываются гидратной коркой; H – общая высота купола; R – радиус купола; mout – массовый расход «вытесненной» смеси из купола; m+ – массовый расход «поступающей» нефти в купол

На этапе 1 купол зафиксирован на высоте 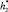, открывается нижнее основание купола и внутрь начинают проникать капли нефти и смешиваться с дизелем. Этот этап продолжается до момента времени t1. Далее, на втором этапе, купол начинает опускаться с некоторой постоянной скоростью, это продолжается, пока купол не достигнет высоты 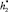. Этап 2 продолжается с момента времени t1 до момента t2. На 3 этапе купол фиксируется на высоте 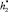и внутрь начинают проникать пузырьки газа, этап продолжается до тех пор, пока толщина слоя газа не достигнет 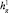, м, время завершения этапа t3. На этапе 4 купол опускается до дна, где фиксируется. На последнем, 5 этапе, который начинается с момента времени t4, рассматривается стационарная работа купола, подключаются трубки для откачки.

Распределение температуры в струе

Поступающие из скважины нефть и газ мигрируют в виде затопленной струи. Определение их температуры и скорости от вертикальной кооррдинаты особенно важно, так как эти параметры используются в качестве начальных при их накоплении в куполе. Распределение температуры и скорости миграции струи подробно рассмотрено в работах [1, 2]. Зная начальную температуру вытекающих углеводородов T0 и температуру воды Tw, а также начальный объемный расход Qe, согласно [5] определим температуру в любом сечении струи Tjet:

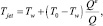(1)

Согласно распределению температуры в струе, определяется высота , на которой струя остывает до температуры гидратообразования. Выше этой высоты пузырьки метана газа начинают покрываться гидратной коркой, превращаясь в гидратную частицу.

До момента, пока нижнее основание купола не пройдет отметку 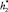, отсчитываемую от дна, будем полагать, что внутрь купола, вытесняя смесь, будут проникать только капли нефти, а при дальнейшем движении купола внутрь начинают проникать и газовые пузырьки.

Этапы работы купола-сепаратора

Этап 1 начинается с момента «открытия» нижнего основания купола tнач, который до этого был загерметизирован. Запишем уравнение сохранения масс для смеси с учетом, что нефть, вытекающая из скважины, полностью попадает в купол и смешивается с дизелем, образуя смесь, которая в свою очередь «вытесняется» нефтью:

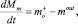(2)

где 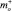– массовый расход поступающей нефти; mout – массовый расход «вытесняемой» смеси; 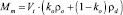– масса смеси; Vt – объем купола; ko – концентрация нефти в смеси. Нижний индекс m соответствует параметрам смеси; o – для параметров нефти. Массовый расход поступающей в купол нефти определяется с учетом известного объемного расхода.

Уравнение сохранения энергии для смеси:

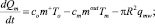
Q_m = c_mT_mM_m, (3)

здесь co, cm – теплоемкости нефти и смеси; qmw – тепловой поток на границе между смесью и водой; Tm, Mm – температура и масса смеси.

Для определения теплового потока qmw будем полагать, что струя углеводородов с вовлеченной водой натекает на неподвижное основание купола и, используя выражение для теплообмена при натекании струи на неподвижную стенку [4], получим

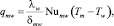
где λ_w – коэффициент теплопроводности воды; δ_mw = 2R₂; Nu_mw – число Нуссельта.

На втором этапе с момента времени t2 купол начинает опускаться с постоянной скоростью w₀. С учетом этого получим уравнение для нахождения изменения координаты нижнего основания купола zn:

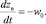
Миграция газового пузырька в слое солярки

На этапе 3 нижнее основание купола достигает и фиксируется на высоте 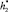, на этой высоте пузырьки газа ещё не покрываются гидратной коркой. Этап 3 начинается с момента времени t3. С этого момента внутрь купола начинают проникать пузырьки газа. Считаем, что газ не смешивается со смесью, а накапливается наверху. Этап 2 продолжается до тех пор, пока толщина слоя газа не станет равной .

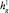Уравнения сохранения для смеси и газа внутри купола запишутся в виде

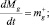
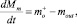(4)

где 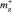– массовый расход поступающего в купол газа; Mg – масса газа в куполе, нижний индекс g относится к газу.

Скорость всплытия для пузырька газа в куполе определяем из уравнения импульсов в безинерционном приближении:

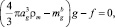(5)

где ag и 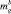– радиус и масса пузырька газа; 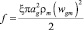– сила гидродинамического сопротивления. Скорость пузырьков газа внутри купола:

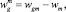
где wgm – относительная скорость пузырьков газа в смеси; wm – скорость смеси. При условии, что купол зафиксирован и неподвижен 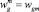. Для определения коэффициента гидравлического сопротивления ξ и числа Рейнольдса Regm для пузырька газа используем следующие выражения:

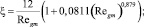
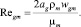(6)

Решая уравнение (5), с учетом (6) найдем скорость всплытия пузырька газа. При параметрах системы: ρ_g = 193 кг/м3, a_g = 5·10^–3 м, – скорость всплытия пузырьков газа в смеси составляет 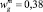м/с.

Запишем уравнение сохранения энергии для пузырька газа, попадающего в купол из струи, движущегося внутри купола:

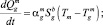
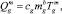(7)

где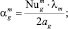

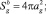
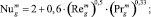
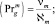
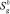– площадь поверхности пузырька.

На рис. 2 представлена зависимость температуры пузырьков газа от вертикальной координаты z. График приведен для этапа 3, времени t3. Начальной температурой пузырька является температура струи на высоте 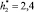м. С увеличением вертикальной координаты z пузырьки газа нагреваются до температуры смеси.

Уравнение сохранения энергии для смеси (7) с учетом пузырьков газа примет вид

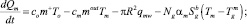Q_m = c_mT_mM_m, (8)

здесь N_g – количество пузырьков газа в слое смеси.

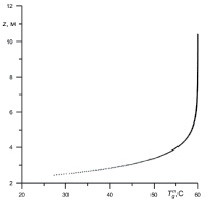
Рис. 2. Зависимость температуры пузырька газа от координаты z

Накопление слоя газа в куполе

При достижении пузырьков газа верхнего основания купола они начинают накапливаться, образуя слой. Уравнение сохранения энергии для слоя газа:

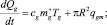Q_g = c_gT_gM_g. (9)

С учетом теплообмена со слоем газа уравнение сохранения энергии для смеси примет вид

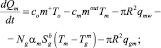
Q_m = c_mT_mM_m, (10)

где q_gm – тепловой поток от слоя газа к слою смеси, который определяется с использованием выражения для теплообмена полуограниченного тела согласно [3]:

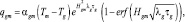(11)

здесь λg – коэффициент теплопроводности для газа; 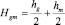– сумма полутолщин слоев газа и смеси; τg – характерное время, отсчитываемое от начала накопления слоя газа; 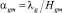– коэффициент теплообмена.

Введем координату раздела слоя газа и смеси zgm с учетом объемного расхода газа:

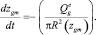(12)

Выводы

В работе описана динамика многофазной затопленной струи, рассмотрен процесс установки купола, предназначенного для накопления газа и нефти, а также рассмотрена задача о миграции пузырьков газа в куполе. Установлено, что пузырек газа, попадающий в купол, наполненный смесью солярки и нефти, нагревается до температуры смеси.

Работа поддержана грантом СФ БашГУ В15-12.

Рецензенты:

Гималтдинов И.К., д.ф.-м.н., профессор, заведующий кафедрой «Прикладная математика и механика», Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак;

Биккулова Н.Н., д.ф.-м.н., профессор кафедры «Общая и теоретическая физика», Стерлитамакский филиал, ФГБОУ ВПО «Башкирский государственный университет», г. Стерлитамак.

Библиографическая ссылка