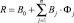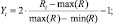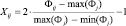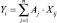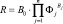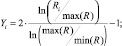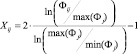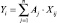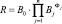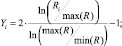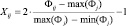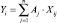Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,798

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чигиринский Ю.Л. 1 Щепетнов И.А. 1 Чигиринская Н.В. 1

---

1 ФГБОУ ВПО «Волгоградский государственный технический университет»

Представлена и обоснована статистическая модель, отражающая взаимосвязи характеристик обрабатываемого материала и технологических режимов лазерного упрочнения с результатами обработки – глубиной поверхностного слоя с измененными физико-механическими свойствами. Модель построена как обобщение результатов исследований отечественных и зарубежных специалистов. Для определения коэффициентов регрессии использована методика полнофакторного производственного эксперимента. При построении аддитивной и мультипликативных моделей обеспечено выполнение комплекса условий Гаусса – Маркова. Показано, в результате сравнения моделей с точки зрения достоверности, адекватности и относительной погрешности, что наиболее корректное описание процесса дает степенная мультипликативная модель. Приведены практические рекомендации относительно применения методов математической статистики для отбора управляющих факторов, построения регрессионных моделей и прогнозирования результатов лазерного упрочнения поверхностей стальных деталей.

Статья в формате PDF

589 KB

качество поверхности

поверхностный слой с измененными физико-механическими характеристиками

лазерное упрочнение

регрессионная модель

полнофакторный эксперимент

управляющие технологические факторы

достоверность

адекватность

1. Евдокимов В.Д. Технология упрочнения машиностроительных. – Николаев: Изд. НГГУ им. Петра Могилы. – 2005. – 352 с.

2. Майоров В.С. Лазерное упрочнение металлов // Лазерные технологии обработки материалов: современные проблемы фундаментальных исследований и прикладных разработок: монография / под ред. В.Я. Панченко. – М.: ФИЗМАТЛИТ, 2009. – 664 с.

3. Марочник сталей [Электронный ресурс] // Центральный металлический портал РФ. – Режим доступа: http://metallicheckiy-portal.ru/marki_metallov/search/.

4. Чигиринский Ю.Л. Особенности применения табличного процессора для построения многофакторных регрессионных моделей / Ю.Л. Чигиринский, Н.В. Чигиринская // Современные инструментальные системы, информационные технологии и инновации: сб. науч. тр. XI междунар. науч.-практ. конф. (19-21 марта 2014 г.). В 4 т. Т. 4 / Юго-Западный гос. ун-т, Московский гос. технол. ун-т «Станкин», Тульский гос. ун-т [и др.]. – Курск, 2014. – C. 315–319.

5. Чигиринский Ю.Л. Стохастическое моделирование в машиностроении: учеб. пособие / Ю.Л. Чигиринский, Н.В. Чигиринская, Ю.М. Быков; ВолгГТУ. – Волгоград: РПК «Политехник», 2002. – 68 с.

6. Чигиринский Ю.Л. Структура электронной таблицы для построения многофакторных регрессионных моделей / Ю.Л. Чигиринский, Н.В. Чигиринская, Л.А. Качалова // Изв. ВолгГТУ. Серия «Прогрессивные технологии в машиностроении». Вып. 11: межвуз. сб. науч. ст. / ВолгГТУ. – Волгоград, 2014. – № 8. – C. 39–41.

7. Capello Ed. and Previtali B. Optimization of production rate in diode laser hardening // Journal of Laser Applications.  –2008. – № 20 (1). – DOI: 10.2351/1.2795747.

Проведен литературный обзор научных работ по лазерному упрочнению поверхностного слоя сталей и чугунов и выявлены основные факторы, которые в конечном итоге влияют в большей мере на требуемые свойства поверхностной закалки.

Виртуальный полнофакторный эксперимент охватывает стали [3] 20ХНЗА, 45ХН2МФА, 12X13, 30X13, 12X17, 15Х25Т, 12Х18Н10Т. Данные для моделирования получены в результате анализа результатов исследований [1, 2, 7 и др.], опубликованных в научных периодических и монографических изданиях. Достоверность средних значений, определенная по критерию Стьюдента, составила не менее 98 % с учетом объемов статистических выборок не менее 140 наблюдений.

Общий массив (табл. 1) исходных данных включает усредненные результаты 140 экспериментов, что образует выборку, репрезентативность которой достаточна для построения аддитивной [4, 5] четырехфакторной (140 > 2⁴ = 16) и мультипликативных (140 > 3⁴ = 81) регрессионных моделей.

Для уточнения списка объясняющих переменных определим (1, 2) коэффициенты корреляции (табл. 2):

коэффициент корреляции «фактор-функция»

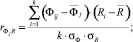(1)

коэффициент интеркорреляции факторов

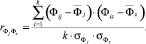(2)

Таблица 1

Усредненные результаты экспериментов

Таблица 2

Корреляция и интеркорреляция

Поскольку коэффициенты интеркорреляции (2) факторов достаточно малы, можно говорить о слабом взаимном влиянии, за исключением коэффициента интеркорреляции фактора 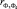. Однако, несмотря на вероятную интеркорреляцию факторов Ф3 и Ф4, многие авторы [1, 2, 7] включают эти факторы в исследования. Аналогично, несмотря на малые значения (табл. 3) коэффициентов корреляции «фактор-функция» (1) для факторов Ф₁ и Ф₃, что практически означает отсутствие линейной зависимости функции отклика от этих факторов, мы также рассматриваем их при моделировании.

Ранее [4, 6] мы обсуждали вопросы, связанные с корректностью построения и возможностью математического анализа регрессионных моделей, в частности с так называемыми условиями Гаусса – Маркова. Для обеспечения выполнения комплекса условий в отношении ортогональности и ротатабельности исходных данных, выполним их нормирование [5] в соответствии с соотношениями (3...5, табл. 3).

В работе рассматриваются три спецификации исходных моделей: линейная, степенная и показательная (экспоненциальная), – наиболее часто применяемые для описания процессов механической и физико-технической обработки. Процедура нормирования (3..5) позволяет привести все модели к одинаковому – линейному – виду в безразмерном координатном пространстве. Использование нормированного координатного пространства позволяет выполнять количественное сравнение коэффициентов регрессии с целью ранжирования технологических факторов по степени воздействия на результат исследуемого процесса.

Фрагмент массива нормированных исходных данных для построения степенной модели и результаты моделирования приведены в табл. 4.

Из представленных (рисунок) графиков видно, что поведение прогнозных линий идентично экспериментальным данным, следовательно, все модели соответствуют реальному процессу. Наиболее близко к экспериментальной кривой лежит график степенной модели, наибольшая погрешность у модели линейной.

В соответствии с неравенством (6) определены значения доверительной вероятности α из условия статистической значимости всех рассматриваемых технологических факторов.

Таблица 3

Преобразования исходной модели

Таблица 4

Параметры степенной модели (нормированные величины)

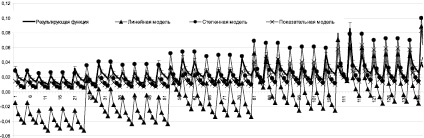
Сравнение экспериментальных данных и результатов моделирования

Статистическая значимость факторов Xj оценивается [5] по критерию Стьюдента 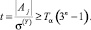(6)

(6)

Проверка адекватности моделей выполнена [5] по критерию Фишера (7) при уровне доверительной вероятности, соответствующем статистической значимости факторов.

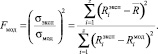(7)

Результаты моделирования приведены в табл. 5, 6.

Сравнение коэффициентов регрессии нормированных моделей позволяет сделать следующее заключение: линейная модель не в полной мере учитывает влияние рассматриваемых технологических факторов, поскольку коэффициент A0 (степень риска) достаточно велик, по сравнению с коэффициентами регрессии технологических факторов.

Ранжированные по степени значимости списки технологических факторов выглядят следующим образом.

Для степенной модели:

– длительность воздействия лазерного луча (время обработки);

– скорость вращения обрабатываемой детали;

– радиус лазерного луча (радиус светового пятна на обрабатываемой поверхности);

– теплофизические характеристики обрабатываемого материала.

Для показательной модели:

– длительность воздействия лазерного луча (время обработки);

– радиус лазерного луча (радиус светового пятна на обрабатываемой поверхности);

– скорость вращения обрабатываемой детали;

– теплофизические характеристики обрабатываемого материала.

Сравнительная оценка погрешности и достоверности (табл. 6) моделей позволяет сформулировать следующие выводы:

1) степенная полнофакторная модель наиболее адекватно описывает процесс лазерного упрочнения поверхностного слоя исследованных сталей;

2) проведенный авторами предварительный анализ литературы о наиболее значимых факторах, влияющих на процесс закалки, вполне согласуется с результатами моделирования.

Таблица 5

Коэффициенты регрессии нормированных моделей

Таблица 6

Параметры моделей в реальном координатном пространстве

Рецензенты:

Мартынов В.В., д.т.н., профессор кафедры «Проектирование технических и технологических комплексов», ФГБОУ ВПО «Саратовский государственный технический университет им. Гагарина Ю.А.», г. Саратов;

Каунов А.М., д.т.н., профессор кафедры «Теория и методика трудового обучения и воспитания», ФГБОУ ВПО «Волгоградский государственный социально-педагогический университет», г. Волгоград.

Библиографическая ссылка