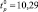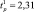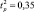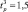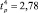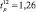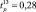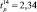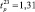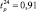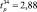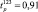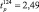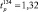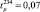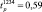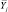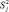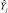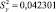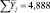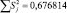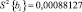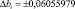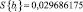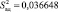В работе [1] для оценки технического состояния электромеханического усилителя рулевого управления (ЭМУ РУ) автомобиля ВАЗ-21703 (LADA Priora) предложен диагностический параметр (ДП) – критерий работоспособности (КР) φ, равный отношению коэффициента усиления момента силы Ку к максимальному току потребления усилителя Imax, а также установлены предельное и предельно допустимое значения КР.
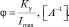 (1)
(1)
В ходе дальнейших экспериментальных исследований проводились стендовые испытания ЭМУ РУ, цель которых заключалась в определении практических значений КР. Факторами, влияющими на КР, являлись установленные в [2] ДП.
Задача эксперимента состояла в получении и проверке интерполяционной формулы для предсказаний значений изучаемого параметра (КР). Как правило, интерполяционная формула представляет собой математическую модель вида
Y = f(X1, X2, X3, …, Xk), (2)
описывающую поведение объекта, которая называется функцией отклика.
Методы исследования: при проведении стендовых испытаний, методика которых описана в [3], было выявлено, что ДП «неравномерное вращение вала электродвигателя» и «температура обмоток электродвигателя» не оказывают существенного влияния на КР. Поэтому для проведения дальнейших исследований были выбраны следующие факторы: максимальный ток потребления, ток потребления при отсутствии момента на входном валу, максимальный компенсирующий момент, время срабатывания ЭМУ. Обработка результатов эксперимента осуществлялась в соответствии с методикой, изложенной в [4].
При исследовании, в области эксперимента устанавливают основные уровни и интервалы варьирования факторов. Интервал варьирования факторов определяется как
 (3)
(3)
Основной (нулевой) уровень рассчитывается по формуле
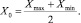 (4)
(4)
Результаты расчета представим в табл. 1.
Далее, зная число факторов, по формуле (5), вычислим общее число экспериментов, которые необходимо провести в данном случае.
N = mk, (5)
где m – число уровней фактора; k – число факторов.
N = 24 = 16.
Факторный эксперимент осуществляют с помощью матрицы планирования, в которой используют кодированные значения факторов. Для исключения систематических ошибок опыты, предусмотренные матрицей планирования необходимо выполнить в случайной последовательности. Поэтому порядок проведения опытов выбран по таблице случайных чисел и представлен в табл. 2.
Для компенсации случайных погрешностей и повышения точности эксперимента произведено равномерное дублирование с числом n параллельных опытов равным 3.
Для каждой строки матрицы планирования по результатам n параллельных опытов найдено среднее арифметическое значение параметра оптимизации:
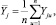 (6)
(6)
где u – номер параллельного опыта; Yju – значение параметра оптимизации в i-м параллельном опыте i-й строки матрицы планирования.
Например, для первой строки матрицы планирования 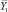 составит
составит
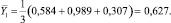
С целью оценки отклонений параметра оптимизации от его среднего значения для каждой строки матрицы планирования вычислена статистическая дисперсия 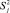 :
:
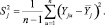 (7)
(7)
Так, 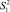 будет равна
будет равна
Таблица 1
Интервал варьирования и основной уровень факторов
|
Наименование и обозначение факторов |
Уровни факторов |
Интервал варьирования, I |
Основной уровень, X0 |
|
|
Верхний |
Нижний |
|||
|
Максимальный ток потребления, X1 |
55 |
0,5 |
27,25 |
27,75 |
|
Ток потребления при отсутствии момента на входном валу, X2 |
0,5 |
0 |
0,25 |
0,25 |
|
Максимальный компенсирующий момент, X3 |
24 |
0 |
12 |
12 |
|
Время срабатывания ЭМУ, X4 |
0,02 |
0,001 |
0,0095 |
0,0105 |
Таблица 2
Порядок реализации опытов
|
Номер опыта матрицы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
Порядок реализации |
Y1 |
14 |
11 |
1 |
15 |
8 |
10 |
6 |
9 |
2 |
16 |
12 |
3 |
7 |
13 |
5 |
4 |
|
Y2 |
10 |
6 |
2 |
13 |
3 |
12 |
8 |
15 |
7 |
1 |
14 |
11 |
5 |
9 |
4 |
16 |
|
|
Y3 |
12 |
7 |
5 |
8 |
13 |
2 |
3 |
14 |
11 |
6 |
10 |
4 |
15 |
9 |
16 |
1 |
|
Ошибка опыта Sj определяется как корень квадратный из дисперсии опыта:
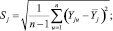 (8)
(8)
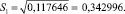
При равномерном дублировании опытов однородность ряда дисперсий проверяют с помощью G-критерия Кохрена, представляющего собой отношение максимальной дисперсии к сумме всех дисперсий:
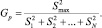 (9)
(9)
В нашем случае
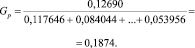
Так как расчетное значение критерия Кохрена Gp = 0,1874 не превышает табличного Gт = 0,3346, то делаем вывод об однородности дисперсий. Учитывая однородность дисперсий, вычислена дисперсия воспроизводимости эксперимента:
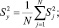 (10)
(10)
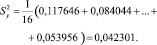
Далее, по результатам эксперимента определены коэффициенты модели. Свободный член b0 найден по формуле
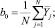 (11)
(11)
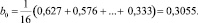
Коэффициенты регрессии рассчитаны по выражению
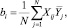 (12)
(12)
где Xij – кодированные значения i-го фактора в j-м опыте.
Так коэффициент регрессии b1 будет равен
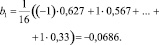
Коэффициенты регрессии, характеризующие эффекты взаимодействия, определены как
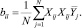 (13)
(13)
Результаты расчета коэффициентов регрессии представлены в табл. 3.
После вычисления коэффициентов модели необходимо проверить их значимость. Проверка значимости коэффициентов осуществляется двумя способами: сравнением абсолютной величины коэффициента с доверительным интервалом и с помощью t-критерия Стьюдента.
При проверке значимости коэффициентов первым способом для определения доверительного интервала необходимо найти дисперсии коэффициентов регрессии.
Дисперсия i-го коэффициента рассчитана по формуле
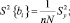 (14)
(14)
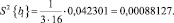
Доверительный интервал ∆bi определен по выражению
∆bi = ±tтS{bi}; (15)
где tт – табличное значение критерия Стьюдента при принятом уровне значимости и числе степеней свободы f, с которым определялась дисперсия 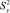 ; S{bi} – ошибка в определении i-го коэффициента регрессии.
; S{bi} – ошибка в определении i-го коэффициента регрессии.
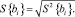 (16)
(16)
При равномерном дублировании опытов число степеней свободы находят как
f = (n – 1)N = (3 –1)∙16 = 32;
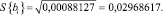
Таблица 3
Значения коэффициентов регрессии
|
b0 = 0,3055 |
b1 = –0,0686 |
b2 = –0,0104 |
b3 = –0,0447 |
b4 = –0,0826 |
|
|
b12 = –0,0375 |
b13 = 0,0083 |
b14 = 0,0696 |
b23 = 0,0389 |
b24 =0,0271 |
b34 = 0,0856 |
|
b123 = 0,0270 |
b124 = 0,0740 |
b134 = –0,0391 |
b234 = –0,0022 |
b1234 = –0,0174 |
При 5 %-м уровне значимости и числе степеней свободы 32 табличное значение критерия Стьюдента составляет tт = 2,04. Тогда доверительный интервал ∆bi будет равен
∆bi = ±2,04∙0,02968617 = ±0,06055979.
Коэффициент считается значимым, если его абсолютная величина больше доверительного интервала. При сравнении полученных значений ∆bi с данными табл. 3 сделан вывод о значимости коэффициентов регрессии b0, b1, b4, b14, b34, b124.
При проверке значимости коэффициентов регрессии вторым способом критерий – tр найден из выражения
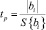 (17)
(17)
и сопоставлен с табличным tт. Коэффициент значим, если tр > tт. Статистически незначимые коэффициенты исключаются из модели. Результаты расчета tр представлены в табл. 4.
После сравнения расчетных значений tр с табличными сделан вывод о значимости коэффициентов регрессии b0, b1, b4, b14, b34, b124.
Таким образом, уравнение регрессии примет вид
Y = b0 + b1X1 + b4X4 + b14X1X4 + b34X3X4 + b124X1X2X4. (18)
После расчета коэффициентов модели и проверки их на значимость определена дисперсия 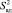 адекватности:
адекватности:
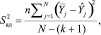 (19)
(19)
где 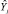 – значение параметра оптимизации, вычисленное по модели для условий j-го опыта; k – число факторов.
– значение параметра оптимизации, вычисленное по модели для условий j-го опыта; k – число факторов.
Так, для первой строки матрицы планирования значение 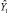 составило
составило
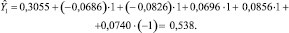
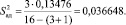
Таблица 4
Значения критерия по выражению
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5
Результаты многофакторного эксперимента
|
Номер опыта |
X0 |
X1 |
X2 |
X3 |
X3 |
Y1 |
Y2 |
Y3 |
|
|
sj |
|
|
1 |
+ |
+ |
+ |
+ |
+ |
0,584 |
0,989 |
0,307 |
0,627 |
0,117646 |
0,342996 |
0,538 |
|
2 |
+ |
– |
+ |
+ |
+ |
0,675 |
0,788 |
0,239 |
0,567 |
0,084044 |
0,289904 |
0,409 |
|
3 |
+ |
+ |
– |
+ |
+ |
0,989 |
0,370 |
0,985 |
0,781 |
0,126900 |
0,356231 |
0,686 |
|
4 |
+ |
– |
– |
+ |
+ |
0,078 |
0,106 |
0,111 |
0,098 |
0,000316 |
0,017786 |
0,262 |
|
5 |
+ |
+ |
+ |
– |
+ |
0,243 |
0,493 |
0,098 |
0,278 |
0,039925 |
0,199812 |
0,367 |
|
6 |
+ |
– |
+ |
– |
+ |
0,116 |
0,105 |
0,470 |
0,230 |
0,043110 |
0,207630 |
0,238 |
|
7 |
+ |
+ |
– |
– |
+ |
0,423 |
0,243 |
0,592 |
0,419 |
0,030460 |
0,174529 |
0,515 |
|
8 |
+ |
– |
– |
– |
+ |
0,152 |
0,078 |
0,081 |
0,104 |
0,001754 |
0,041885 |
0,090 |
|
9 |
+ |
+ |
+ |
+ |
– |
0,086 |
0,384 |
0,122 |
0,197 |
0,026457 |
0,162657 |
0,210 |
|
10 |
+ |
– |
+ |
+ |
– |
0,061 |
0,137 |
0,423 |
0,207 |
0,036436 |
0,190882 |
0,064 |
|
11 |
+ |
+ |
– |
+ |
– |
0,092 |
0,088 |
0,130 |
0,103 |
0,000537 |
0,023180 |
0,062 |
|
12 |
+ |
– |
– |
+ |
– |
0,100 |
0,123 |
0,439 |
0,221 |
0,035884 |
0,189432 |
0,212 |
|
13 |
+ |
+ |
+ |
– |
– |
0,384 |
0,403 |
0,072 |
0,286 |
0,034544 |
0,185861 |
0,382 |
|
14 |
+ |
– |
+ |
– |
– |
0,093 |
0,161 |
0,149 |
0,134 |
0,001317 |
0,036295 |
0,235 |
|
15 |
+ |
+ |
– |
– |
– |
0,403 |
0,439 |
0,061 |
0,301 |
0,043524 |
0,208624 |
0,234 |
|
16 |
+ |
– |
– |
– |
– |
0,439 |
0,067 |
0,494 |
0,333 |
0,053956 |
0,232285 |
0,383 |
|
Gp = 0,1874 |
|
|
|
|||||||||
|
Gт = 0,3346 |
|
|
Fр = 0,866 |
Fт = 2,1 |
||||||||
|
f = 32 |
|
|
tт = 2,04 |
|||||||||
Результаты исследования и их обсуждение
Результаты эксперимента по установлению влияния диагностических параметров ЭМУ РУ на критерий работоспособности показаны в табл. 5.
Далее выполнена проверка гипотезы об адекватности полученной математической модели [5]. Для этого использовался критерий Фишера:
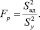 (20)
(20)
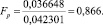
Поскольку 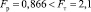 для принятого уровня значимости и соответствующем числе степеней свободы, то модель считаем адекватной.
для принятого уровня значимости и соответствующем числе степеней свободы, то модель считаем адекватной.
Вывод
В результате экспериментальных исследований по установлению рабочих характеристик ЭМУ РУ ВАЗ-21703 получены практические значения КР и соответствующие им величины факторов. В процессе стендовых испытаний выявлено слабое влияние ранее предложенных ДП «неравномерное вращение вала электродвигателя» и «температура обмоток электродвигателя» на исследуемый показатель работоспособности, поэтому в факторном анализе они не учитывались. По результатам эксперимента определены коэффициенты регрессионной модели и осуществлена проверка их значимости. Степень влияния различных диагностических параметров ЭМУ РУ на критерий его работоспособности отражена в уравнении регрессии, которое успешно прошло проверку на адекватность. Факторы «максимальный ток потребления», «максимальный компенсирующий момент», а также «время срабатывания ЭМУ» в наибольшей степени влияют на КР.
Рецензенты:
Гоц А.Н., д.т.н., профессор кафедры «Тепловые двигатели и энергетические установки», ФГБОУ ВПО «Владимирский государственный университет им. Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир;
Кульчицкий А.Р., д.т.н., профессор, главный специалист, ООО «Завод инновационных продуктов КТЗ», г. Владимир.
Библиографическая ссылка
Денисов И.В., Смирнов А.А. ФАКТОРНЫЙ ЭКСПЕРИМЕНТ ПО УСТАНОВЛЕНИЮ СТЕПЕНИ ВЛИЯНИЯ ПАРАМЕТРОВ ЭЛЕКТРОМЕХАНИЧЕСКОГО УСИЛИТЕЛЯ РУЛЕВОГО УПРАВЛЕНИЯ ВАЗ-21703 НА КРИТЕРИЙ ЕГО РАБОТОСПОСОБНОСТИ // Фундаментальные исследования. 2015. № 5-2. С. 289-293;URL: https://fundamental-research.ru/ru/article/view?id=38209 (дата обращения: 28.02.2026).