Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Платонова Е.C. 1 Бучинскас В. 2 Юров В.М. 3

---

1 Карагандинский государственный технический университет

2 Вильнюсский технический университет им. Гедеминаса

3 Карагандинский государственный университет им. Е.А. Букетова

В работе рассмотрена модель образования коррозионного пятна на металле с точки зрения статистической неравновесной термодинамики. Центры коррозии (химически активные атомы поверхности металла) рассматриваются как система невзаимодействующих частиц, погруженная в термостат (металл). Вычисляется вероятность диссипативных процессов, обусловленная взаимодействием ансамбля частиц с термостатом. На этой основе вычисляется функция отклика системы на внешнее воздействие (процесс коррозии). В рамках такой модели показана связь площади коррозионного пятна с энергией Ферми для чистых металлов. У тех металлов, у которых энергия Ферми больше, больше и коррозионная стойкость. Показано также, что коррозионная стойкость чистых металлов возрастает с ростом их температуры плавления. Получена формула для скорости процесса коррозии, которая включает в себя экспериментально определяемые параметры.

Статья в формате PDF

458 KB

коррозия

коррозионное пятно

металл

окисление

энергия Ферми

1. Азаренков Н.А., Литовченко С.В., Неклюдов И.М., Стоев П.И. Коррозия и защита металлов. Часть 1. Химическая коррозия металлов. – Харьков: ХНУ, 2007. – 187 с.

2. Ашкрофт Н., Мермин Н. Физика твердого тела. – Т 1. – М.: Мир, 1979. – 399 с.

3. Таблицы физических величин. Справочник / под ред. академика И.К. Кикоина. – М.: Атомиздат, 1976. – 1008 с.

4. Халенов О.С., Коровкин М.В., Юров В.М. Термодинамические аспекты электрической проводимости кристаллов и твердых растворов // Фундаментальные исследования. – 2014. – № 6, Часть 7. – С. 1384–1389.

5. Юров В.М. Термодинамика люминесцирующих систем // Вестник КарГУ, сер. Физика. – 2005. – № 3 (39). – С. 13–15.

6. Юров В.М., Колесников В.А., Исмаилов Ж.Т., Байсагов Я.Ж. Термодинамика информационно-измерительных систем: монография. – Караганда: Изд-во Казахстанско-Российского ун-та, 2013. – 112 с.

7. Baroux B. The kinetics of pit generation on stainless steel // Corrosion science. – 1988. – Vol. 28, № 10. – P. 969–986.

8. Jurov V.M. Superfecial tension of pure metals // Eurasian Physical Technical journal. – 2011. – Vol. 8. – № 1(15). – P. 10–14.

9. Provan J.W., Rodriguez E.S. Development of a Markov description of pitting corrosion // Corrosion (USA). – 1989. – Vol. 45, № 3. – P. 178–192.

10. Strutt I.E., Nicholls and Barbier B. The prediction of corrosion by statistical analysis of corrosion profiles // Corrosion science. – 1985. – Vol. 25, № 5. – P. 305–3l6.

Первопричиной коррозии металлов является их термодинамическая неустойчивость в различных средах при данных внешних условиях, поэтому роль термодинамики в теории коррозии достаточно велика [1]. Однако методы классической термодинамики с использованием термодинамических потенциалов не могут адекватно описать сложный и многостадийный процесс коррозии металла. Поэтому привлекаются методы химической кинетики [7], статистические [10], стохастические [9] и другие методы.

В настоящей работе мы используем метод неравновесной термодинамики для описания коррозии металла. Метод является довольно общим и зарекомендовал себя неплохо при рассмотрении процессов различной природы, где наблюдается отклик системы на внешнее воздействие [4–6].

Термодинамическая модель

Мы рассмотрим, следуя работе [5], вопрос отклика подсистемы дефектов (центров коррозии) в металлах на внешнее воздействие (окислительный процесс на поверхности металла) с позиций неравновесной статистической термодинамики.

Дефекты поверхности металла (центры коррозии) будем рассматривать как систему невзаимодействующих частиц, погруженную в термостат. Квантовые переходы, обусловленные взаимодействием дефектов с термостатом, будут диссипативными (с вероятностью Р) в отличие от взаимодействия с внешним полем (с вероятностью F). Поскольку в процессе коррозии подсистема дефектов обменивается с термостатом только энергией, то соответствующий им ансамбль частиц будет каноническим. В этом случае выражение для статистической энтропии имеет вид

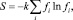(1)

где f_i – функция распределения; k – постоянная Больцмана.

Дифференцируя (1) по времени и преобразуя, получим

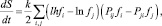(2)

где P_ij – вероятность перехода из начального i (с энергией Ei) в возбужденное состояние j (с энергией Ej).

Для диссипативных процессов принцип детального равновесия имеет вид

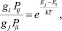(3)

где g_i, g_j – статистические веса для уровней E_i и E_j.

Тогда (2) примет вид

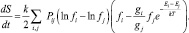(4)

Опуская промежуточные вычисления (см. [5]), пренебрегая малыми членами и заменяя в (4) сумму интегралом, получим

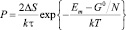, (5)

где ΔS – изменение энтропии в диссипативном процессе; E_m – среднее значение энергии основного состояния дефектов; τ – время релаксации; N – среднее число дефектов; G⁰ – энергия Гиббса термостата.

Для функции отклика Ф системы на внешнее поле имеем

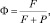(6)

где Р – вероятность диссипативного процесса и определяется (5); F определяет вероятность перехода в возбужденное состояние за счет первичного внешнего поля, причем F = 1/τ_р, где τ_р – время жизни возбужденного состояния. С учетом (5) выражение (6) примет вид

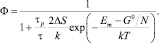(7)

Коррозионная стойкость чистых металлов

Если в качестве функции отклика Ф взять площадь коррозионного пятна S, то после линеаризации (7), получим

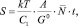(8)

где А – работа «внешних сил»; Т – температура; G⁰ – потенциал Гиббса массивного образца металла; 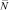– среднее число центров коррозии; t – время протекания процесса коррозии (t = τ); k – постоянная Больцмана, С₁ – постоянная.

Работа «внешних сил» равна изменению стандартного термодинамического потенциала ΔG_T, который является основой термодинамики коррозии и может быть определен через константу химического равновесия К_p по формуле [1]:

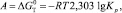(9)

Потенциал Гиббса массивного образца металла совпадает с его химическим потенциалом или энергией Ферми, т.е. G⁰ = E_F. Для расчета энергии Ферми воспользуемся моделью Зоммерфельда, в которой распределение электронов по скоростям описывается статистикой Ферми – Дирака [2]:

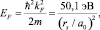(10)

где k_F – волновой вектор Ферми; r_s – радиус сферы, объем которой равен объему, приходящемуся на один электрон проводимости; m – масса электрона; а₀ – радиус атома водорода.

В соответствии с этой моделью rs вычисляется по формуле

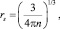(11)

где n – плотность электронов проводимости, которая равна: 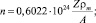А – относительная атомная масса металла; Z – число электронов на внешнем уровне металла; rm – массовая плотность метала (г/см3).

Результаты расчета энергии Ферми представлены в табл. 1.

Таблица 1

Энергия Ферми некоторых металлов

Из формулы (8) и табл. 1 видно, что коррозионная стойкость наименьшая для щелочных и щелочноземельных металлов, имеющих наименьшую энергию Ферми. Однако в формулу (8) входит большее число параметров и судить о коррозионной стойкости только по величине энергии Ферми нельзя.

На самом деле коррозия начинается с поверхностного слоя и поэтому в формуле (8) следует сделать замену –

G⁰ = σ∙S₀,

где σ – поверхностное натяжение; S₀ – удельная поверхность.

Как показано в работе [8], величина поверхностного натяжения металла связана с его температурой плавления соотношением: σ = 10^–4 Т_пл. По данным работы [3], эти значения приведены в табл. 2.

Из табл. 2 следует, что коррозионная стойкость чистых металлов возрастает с ростом температуры плавления. Беря в качестве функции отклика в (8) толщину корродируемого слоя h, для скорости коррозии (v_кор = h/t), которая определяется экспериментально, окончательно получим выражение

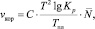(12)

где постоянная С включает все постоянные величины из предыдущих формул.

Таблица 2

Температура плавления некоторых чистых металлов [10]

Заключение

Несмотря на простоту формул (8) и (12) они могут быть полезными для исследования процессов коррозии любых конструкционных материалов, поскольку включают в себя легко определяемые в эксперименте параметры.

Рецензенты:

Портнов В.С., д.т.н., профессор, начальник УПО, Карагандинский государственный технический университет, г. Караганда;

Жакатаев Т.А., д.т.н., старший преподаватель кафедры ММ и Н, Карагандинский государственный технический университет, г. Караганда.

Работа поступила в редакцию 17.03.2015.

Библиографическая ссылка