Во всем мире в сложных энергосистемах с протяженной и развитой электрической сетью регулярно происходят аварийные процессы различного уровня сложности. Исследование аварийных процессов в неоднородных электротехнических и электроэнергетических комплексах является актуальной задачей, которая прорабатывалась многими авторами [1–6, 9, 10].
В работе [5] приведены исследования влияния неоднородности на возникновение чувствительных – сенсорных и слабых областей в ЭС. Изложены методы, использующие для анализа поведения ЭС при наличии возмущений математические инструменты в виде: спектрального, сингулярного, структурного и кластерного анализов. В результате исследования нахождения сенсоров и слабых мест производятся расчеты по оценке допустимости режима, формулируется постановка задач применения вышеперечисленных инструментов к задачам управления режимами ЭС с рассмотрением вопросов усиления слабых мест, выбора состава контролируемых параметров, формирования существенных ограничений и исследования переходных режимов на основе неоднородности.
В работе [2–4] излагаются задачи, приводящие к необходимости разработки методов глобального анализа режимов ЭС. В поставленных задачах производится исследование особенностей на поверхности предельных режимов. Доказывается влияние топологии на существование и структуру опасных областей. Показывается, что при отключении нескольких ветвей сети на поверхности предельных режимов возникают многообразия особых точек, которые определяются по методу L-функции. Данный метод позволяет исследовать режимы ЭС в пространстве полных мощностей с учетом параметров сети и статических характеристик нагрузки. Метод L-функции не нашел широкого применения в практике по причине внешней сложности по отношению к балансовым методам оценки надежности работы энергосистем.
При исследовании аварийных процессов в неоднородных ЭС исследуются в том числе и каскадные процессы (КП). В работе [6] предлагается обобщенный сценарий КП, согласно которому результат аварии отождествляется с потерей устойчивости и неуправляемостью аварийным процессом. Данный сценарий применяется к анализу Московской аварии 2005 г., в котором постепенное ослабление сети за счет последовательно возникающих перегрузок и в результате этого происходящих отключений линий 220 кВ, отходящих от подстанции Очаково, каскадным процессом не считается, как и происходящее в результате перераспределение потоков мощности, перегрузки других линий распределительной сети.
В исследовании [1] производится определение чувствительности узлов ЭС на основной частоте и высших гармониках. Определяется чувствительность напряжений при изменении параметра нагрузки в узлах. В результате доказано, что узлы с наибольшей чувствительностью более других подвержены нарушениям по гармоническому составу кривой напряжения, а нелинейная нагрузка, присоединенная к таким узлам, вызывает наибольшие гармонические искажения.
Несмотря на развитие теории и инструментов, направленных на повышение надежности и живучести электротехнических и электроэнергетических комплексов, ежегодно в мире происходят аварии, в том числе каскадного типа, влекущие за собой существенные по масштабу моральные и материальные потери. Этот факт обуславливает актуальность исследования возникновения и развития каскадных процессов, а также явную потребность в разработке инструмента, направленного на предотвращение возникновения подобных динамических явлений аварийного характера в ЭС.
Сегодня для формирования стабильной работы ЭС применяется методика определения устойчивости системы на критериальном интервале N-X от критического состояния системы. В зависимости от различных способов расчета балансов активной мощности, в России в рамках применяемого критерия надежности N – 1 расчет максимально допустимого перетока (МДП) производится в соответствии с методическими указаниями по устойчивости электроэнергетических систем (ЭЭС) [8]. В основе этой методики лежат 5 критериев (вариантов) расчета МДП, в соответствии с которыми производится формирование режимов. Для данного метода характерна существенно обобщенная оценка состояния системы по отношению влияния перегрузок элементов сети и возникающих каскадных процессов к критическому (предельному) состоянию системы. В результате методика расчета МДП, принятая в соответствии с методическими указаниями [8], закладывает для ЭЭС запас надежности, который в конечном итоге отражается на неэкономичном принятии решений – как по развитию сети, так и по формированию и ведению режимов, что является одним из факторов завышения тарифов для потребителей.
В данном исследовании производились расчеты по разработанной методике определения влияния неоднородности системных и режимных параметров ЭС на разработанные в [9] механизмы возникновения и развития каскадных аварийных процессов [9]. Методика уточняет соотношение областей существования режимов и возможности переходов между ними.
В неоднородном пространстве ЭС существенны для режимов с возможностью развития каскадных процессов следующие области:
– область допустимых значений режимов (ОДЗР), в которой параметры находятся в допустимой зоне;
– область недопустимых значений режима (ОНЗР) для конкретных режимных параметров ЭС;
– при определенных неоднородностях в ЭС существуют области (области каскадных процессов – ОКП) между ОДЗР и ОНЗР, при попадании в которые процесс перехода в ОНЗР становится самопроизвольно осуществимым [9].
Следовательно, задача исследования при формировании и ведении режимов в неоднородных ЭС состоит в определении режима, отстоящего от ОНЗР и ОКП на критериальном расстоянии N-X, если из ОКП режим переходит в ОНЗР. То есть в ОДЗР среди квазистационарных состояний практически важным являются опасные режимы в пограничной области критериальной близости до ОНЗР, а также в области каскадных процессов (ОКП), где самопроизвольный каскадный процесс может завершиться в ОДЗР или ОНЗР, в зависимости от неоднородности параметров состояния и режима ЭС [10].
Переход режима ЭС в ОНЗР означает, что значения зависимых переменных Xk превышают максимальные или минимальные предельно допустимые критериальные значения, приводящие к нарушению устойчивости в широком смысле:
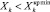 или
или 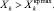
Чаще всего как в системообразующей, так и в распределительной электрической сети примером таких переменных является напряжение в узлах 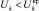 , приводящее к нарушению устойчивости по напряжению, где Uk – расчетное (фактическое) значение напряжения в узлах ЭС,
, приводящее к нарушению устойчивости по напряжению, где Uk – расчетное (фактическое) значение напряжения в узлах ЭС, 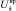 – предельное (критическое) значение напряжения в узлах.
– предельное (критическое) значение напряжения в узлах.
Переход режима ЭС в ОКП означает, что значения группы зависимых переменных Xp последовательно превышают критериальные (предельные) значения 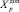 , что для них является выводом (отключением) этого элемента ЭС – носителя этого значения из схемы ЭС, приводящее в результате к самопроизвольному пошаговому «сползанию» режима из ОДЗР в ОНЗР [9].
, что для них является выводом (отключением) этого элемента ЭС – носителя этого значения из схемы ЭС, приводящее в результате к самопроизвольному пошаговому «сползанию» режима из ОДЗР в ОНЗР [9].
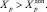
Примером таких переменных можно считать значение токов в элементах ЭС:
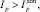
где Ip – расчетное значение тока; 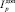 – предельно допустимое значение тока.
– предельно допустимое значение тока.
Для любой электротехнической системы неоднородность распределенных системных и режимных параметров принципиально влияет на возможность развития в ЭС КП. В исследуемой системе (рис. 1) использована возможность моделирования КП практически в любой последовательности с изменением начальных параметров неоднородной ЭС.
В общем случае математическая модель установившегося режима является системой алгебраических нелинейных уравнений с комплексными коэффициентами и переменными:
F(X, Y, Z) = 0, (1)
где F = [f1, f2, ..., fn] – n-мерная вектор-функция, отвечающая уравнениям узловых напряжений, записываемая в форме баланса токов или мощностей; X = [x1, x2, ..., xm] – искомый вектор регулируемых (зависимых) переменных, в которые входят действительные и мнимые составляющие или модули и фазы узловых напряжений и токов в ветвях, а также может входить и значение частоты в энергосистеме; Y = [y1, y2, ..., yd] – заданный вектор базовых параметров (независимых переменных) состоящие из сопротивления и проводимости ветвей и т.п.; Z = [z1, z2, ..., zg] – векторы управляющих параметров (переменных, воздействующих на ЭС), примером управляющих параметров являются активные и реактивные мощности генераторов и нагрузок, зафиксированные в отдельных узлах сети модули напряжений (Pг, Qг, Pн, Qн, 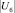 ) и т.п., посредством которых оператор имеет возможность воздействовать на ЭС.
) и т.п., посредством которых оператор имеет возможность воздействовать на ЭС.
В результате мы получаем функцию зависимости X = f(Y, Z).
При этом регулируемые (зависимые) переменные X состоят из следующих групп:
а) переменные, являющиеся индикаторами нарушения устойчивости режима ЭС в широком смысле:
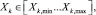
где Xk – параметр ЭС; Xk min и Xk max – предельно допустимые значения для практических критериев устойчивости;
б) переменные, превышение предельно допустимых значений которых приводит к возникновению КП:
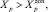
где Xp – параметр, превышение предельно допустимого значения которого приводит к возникновению КП; 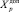 – предельно допустимое значение;
– предельно допустимое значение;
в) прочие зависимые переменные:
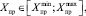
где Xпр – прочие зависимые переменные, предельно допустимые значения которых не приводят к нарушению устойчивости режима ЭС или возникновению КП; 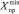 и
и 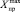 – предельно допустимые значения.
– предельно допустимые значения.
В вычислительных экспериментах для расчета уравнений установившегося режима (УУР) использовался сертифицированный ПК «RASTR WIN», достоверность расчетов УУР которого подтверждается многолетним использованием и применением его системным оператором единой энергосистемы России. В данном ПК «RASTR WIN» в качестве метода расчета УУР использован метод Ньютона, обеспечивающий, как правило, наиболее быструю сходимость при решении систем нелинейных уравнений.
Математическими соотношениями, положенными в основу метода Ньютона, являются уравнения баланса мощностей для k-го узла [7]:
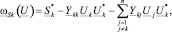
где функция 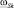 соответствует небалансу мощности в k-м узле; n – число узлов сети;
соответствует небалансу мощности в k-м узле; n – число узлов сети; 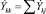 – собственная проводимость k-го узла; Ykj – проводимость ветвей, подходящих к j-му узлу;
– собственная проводимость k-го узла; Ykj – проводимость ветвей, подходящих к j-му узлу; 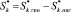 – узловая мощность k-го узла.
– узловая мощность k-го узла.
При исследовании многопараметрического пространства ЭС формировались режимы работы при разнообразных способах распределения нагрузки и генерации между узлами для определения и формирования самопроизвольных КП. Для этого применялись методы утяжеления режимов, состоящие в увеличении генерации на станциях, и потребления в заданных узлах нагрузки. Предельные возможности, которые ограничивают такое увеличение, определяются по условиям существования режима либо ограничениями уровней напряжений в узлах и пропускными способностями ветвей сети (ЛЭП, трансформаторов и т.п.). Математически процесс увеличения генерации и нагрузок в узлах можно описать введением параметра утяжеления режима в УУР [4]:
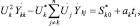 (2)
(2)
где ti > 0, ti = 1, 2, ..., i, при ti = 0 система (2) имеет решение, соответствующее исходному режиму {Sk0}. В (2) ak – весовой коэффициент увеличения или уменьшения узловых мощностей.
Утяжеление режима осуществляется увеличением параметра ti. Если при 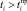 режим системы (2) не существует, то значение
режим системы (2) не существует, то значение 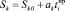 является значением управляющего параметра, который характеризует переход системы в ОНЗР из ОДЗР. Если при ti > ti + 1 режим переходит в ОКП, то возникает каскадный процесс, определяющийся соответствующей неоднородностью сети, с окончанием в ОДЗР или ОНЗР.
является значением управляющего параметра, который характеризует переход системы в ОНЗР из ОДЗР. Если при ti > ti + 1 режим переходит в ОКП, то возникает каскадный процесс, определяющийся соответствующей неоднородностью сети, с окончанием в ОДЗР или ОНЗР.
Ниже представлена обобщенная схема ЭС (рис. 1), состоящая из 25 узлов и 40 ветвей. С заданным балансирующим узлом 1–1, номинальным напряжением сети Uном = 115 кВ. В данной схеме начальные условия сформированы так, что развитие отключений элементов (ветвей) схемы происходит самопроизвольно пошагово в виде каскадного процесса по траектории: 1 шаг – 21–22, 2 шаг – 17–22, 3 шаг – 17–18, 4 шаг – 13–18, 5 шаг – 13–14, 6 шаг – 8–9, 7 шаг – 3–4 (рис. 1). При этом на последнем шаге при отключении ветви 3–4 происходит отключение 13 узлов сети. На приведенном рис. 1 показан момент существования схемы на 7 шаге КП после самопроизвольного пошагового последовательного отключения 6 элементов. На рис. 1 интенсивность окрашивания показывает загруженность элементов по току.
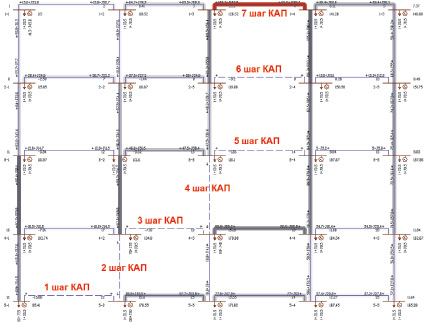
Рис. 1. Схема электротехнической сети с пошаговым развитием каскадного процесса
При моделировании каскадного процесса (рис. 1) были заданы следующие начальные условия в узлах:
– потребление: узел 17 Pн = 70 МВт, Qн = 35 Мвар; узел 21 Pг = 100 МВт, Qг = 35 Мвар; остальные узлы Pн = 1 МВт, Qн = 0,5 Мвар;
– генерация: узел 18 и 22 Pг = 80 МВт, Qг = 40 Мвар, остальные узлы Pг = 1 МВт, Qг = 0,5 Мвар;
– балансирующий узел 1–1;
– напряжение критическое Uкр = 0,7Uном;
– триггерное событие: увеличение нагрузки в узле 21 на Pн = 15 МВт, Qн = 7,5 Мвар.
Длительно допустимые и расчетные текущие значения токов в ветвях (строки) на каждом шаге каскадного процесса (столбцы) указаны в таблице. Столбец Iн.у указывает на значения токов в элементах каскадного процесса в момент времени установившегося режима (до возникновения триггерного события).
В момент времени t0 электротехническая система находилась в ОДЗР. В момент времени t1 произошло триггерное возмущение: в узле 21 повысилось потребление – Pн = 15 МВт, Qн = 7,5 Мвар. Данное возмущение в неоднородной сети привело к набросу тока на ряд элементов ΔIij, в т.ч. 21–22 ΔI21-22 = 68 А, так, что результирующий ток Iij + ΔIij на этом элементе превысил длительно допустимое значение Iдоп ij и привел к переходу режима в ОКП (таблица) с возможностью последующего пошагового самопроизвольного сползания в ОНЗР 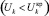 . В применяемой математической модели токовая загрузка элемента ЭС выше допустимой приводит к его выводу из схемы (отключению). Тогда необходимым условием существования ОКП является неравенство (3), которое должно выполняться на каждом следующем шаге аварийного отключения [9].
. В применяемой математической модели токовая загрузка элемента ЭС выше допустимой приводит к его выводу из схемы (отключению). Тогда необходимым условием существования ОКП является неравенство (3), которое должно выполняться на каждом следующем шаге аварийного отключения [9].
Iij + ΔIij > Iдоп ij. (3)
Невыполнение неравенства приводит к останову каскадного процесса с последующим переходом в ОДЗР или в ОНЗР.
Токи в элементах электротехнической сети при пошаговом развитии каскадного процесса
|
Ветви КП |
Iн.у |
1 шаг |
2 шаг |
3 шаг |
4 шаг |
5 шаг |
6 шаг |
7 шаг |
|
21–22, Iдоп ≤ 330 |
316 |
384 |
||||||
|
17–22, Iдоп ≤ 390 |
163 |
174 |
395 |
|||||
|
17–18, Iдоп ≤ 520 |
252 |
260 |
313 |
548 |
||||
|
13–18, Iдоп ≤ 520 |
131 |
129 |
160 |
200 |
522 |
|||
|
13–14, Iдоп ≤ 450 |
75 |
76 |
89 |
120 |
185 |
483 |
||
|
8–9, Iдоп ≤ 520 |
106 |
106 |
113 |
129 |
189 |
294 |
591 |
|
|
3–4, Iдоп ≤ 605 |
138 |
138 |
138 |
143 |
184 |
232 |
381 |
927 |
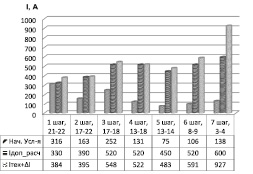
Рис. 2. Пошаговое развитие каскадного процесса в обобщенной ЭС
Схематично пошаговое развитие каскадного процесса (таблица) представлено на рис. 2, где 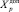 для элемента, имеющего на соответствующем шаге
для элемента, имеющего на соответствующем шаге 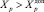 , представлена гистограммами с горизонтальной штриховкой. Гистограммы с косой штриховкой указывают значение Xp для соответствующего элемента в ОДЗР, до возникновения триггерного возмущения, повлекшего за собой переход в ОКП. Волнистой штриховкой представлены гистограммы, указывающие значения Xp для соответствующего элемента на шаге КП, когда на этом элементе становится
, представлена гистограммами с горизонтальной штриховкой. Гистограммы с косой штриховкой указывают значение Xp для соответствующего элемента в ОДЗР, до возникновения триггерного возмущения, повлекшего за собой переход в ОКП. Волнистой штриховкой представлены гистограммы, указывающие значения Xp для соответствующего элемента на шаге КП, когда на этом элементе становится 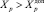 и элемент выводится из схемы (отключается).
и элемент выводится из схемы (отключается).
На основе данной методики возможен анализ и выявление топологических закономерностей по определению влияния неоднородности режимных и системных параметров ЭС на формирование ОДЗР, ОКП и ОНЗР.
Таким образом, разработанная методика определения влияния неоднородности электротехнических систем на возникновение КП позволяет создать совокупность сетевых и режимных параметров, при которых, в пределах соответствующего критерия, возникает самопроизвольно развивающийся КП, переходящий, в зависимости от конкретной неоднородности сети, в ОДЗР или ОНЗР вне зависимости от критериальной близости начальной совокупности параметров режима к предельному. Методика позволяет учитывать влияние неоднородности на возникновение и развитие аварийных процессов в ЭС и принимать экономически и технологически обоснованные решения по развитию энергосистем, формированию и ведению их режимов при обеспечении требуемой надежности.
Рецензенты:Саттаров Р.Р., д.т.н., профессор, кафедра электромеханики, ГОУ ВПО УГАТУ, г. Уфа;
Гизатуллин Ф.А., д.т.н., профессор, кафедра электромеханики, ГОУ ВПО УГАТУ, г. Уфа.
Работа поступила в редакцию 18.03.2015.
Библиографическая ссылка
Шахмаев И.З., Гайсин Б.М. О РАЗВИТИИ КАСКАДНЫХ ПРОЦЕССОВ В ЭЛЕКТРОТЕХНИЧЕСКИХ И ЭЛЕКТРОЭНЕРГЕТИЧЕСКИХ КОМПЛЕКСАХ // Фундаментальные исследования. 2015. № 2-9. С. 1871-1876;URL: https://fundamental-research.ru/ru/article/view?id=37324 (дата обращения: 10.02.2026).



