Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,798

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Чуйко А.Д. 1 Христосенков С.А. 1 Петуров В.И. 1

---

1 Забайкальский институт железнодорожного транспорта – филиал ФГБОУ ВПО «Иркутский государственный университет путей сообщения» Федерального агентства железнодорожного транспорта

Проведен анализ влияния распределения плотности тока в коллекторной пластине на нагрев коллектора тягового электродвигателя. Были приняты следующие допущения в модели, такие как сила нажатия щетки на коллектор, внешние факторы (пыль, газ, избыточная влажность, низкая температура), марка щётки не подходит к условиям работы машины (слишком толстый слой политуры, слишком большая или слишком малая плотность тока в щётках, вентиляция и т.д.), двухмерная модель системы «коллектор – щетка – петушок» вместо трехмерной. По результатам моделирования получены следующие выводы. При обосновании выбора источников выделения тепла необходимо учитывать факт распределения плотности тока в коллекторной пластине. Большинство методик расчетов распределения тепла в коллекторе (например, метод тепловых схем замещения) не учитывают геометрию коллектора и являются менее точными по сравнению с методом конечных элементов. Максимальное тепловыделение при качественной пайке составляет 496,717 Вт, что соответствует плотности тока равной 168,475 А/м2. С учетом вышеизложенного возникает необходимость в расчете модели с использованием метода конечных элементов в программной среде трехмерного моделирования с целью исследования влияния рассмотренного типа дефекта на нагрев коллектора. По полученным данным моделирования выявлены условные тепловые зоны, зависящие от плотности тока в рассматриваемых участках.

Статья в формате PDF

972 KB

коллектор

плотность тока

нагрев

тяговый электродвигатель

1. Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975. – 541 с.

2. Петуров В.И., Четвериков С.В. Математическое моделирование при исследовании диэлектрических характеристик изоляции электрических сетей напряжением 6, 10 кВ // Современные технологии. Системный анализ. Моделирование. – 2014. – № 3 (43). – С. 68–71.

3. Трофимова Т.И. Курс физики: учеб. пособ. для вузов / Трофимова Т.И. – 15-е изд. – М.: Академия, 2007. – 560 с.

4. Тютрина С.В., Кузнецова Н.С., Бурнашова Н.Н. Спектральная характеристика силикатов Забайкальского края и композитов на их основе, полученных при воздействии ультразвуковых колебаний // Фундаментальные исследования. – 2012. – № 9. – С. 460–464.

5. Фоменко В.К. Разработка технологии тепловизионного контроля технического состояния якорей тяговых электродвигателей локомотивов: дис. … канд. техн. наук. – Омск, 2008. – 143 с.

6. ЦТ-ЦТВР-4782 – Правила ремонта электрических машин электроподвижного состава.

7. Четвериков С.В., Петуров В.И. Теоретическое исследование возможностей повышения стойкости инструмента из композита // Современные проблемы науки и образования. – 2014. – № 2; URL: http://www.science-education.ru/116-12432.

8. Чуйко А.Д. Анализ существующих методов диагностирования паянных соединений петушков коллектора тягового электродвигателя // Управление, эксплуатация и ремонт железнодорожных узлов и агрегатов: межвузовский сборник научных трудов. – Чита: ЗабИЖТ, 2009 г.

9. Чуйко А.Д. Расчет теплового поля коллектора в программной среде Elcut 5.6 // Инновации и современные технологии экономике и транспорту: межвузовский сборник научных трудов. – Чита: ЗабИЖТ, 2013.

Тяговые электродвигатели выходят из строя из-за проявления различных неисправностей и типов дефектов. Согласно статистическим данным по отказам тяговых электрических двигателей (ТЭД) одной из наиболее часто встречающихся разновидностей повреждений ТЭД является выплавление припоя из петушков коллектора [8]. Работы в области разработки методов и средств диагностирования тяговых электродвигателей выполнялись учеными и специалистами ВНИИЖТ, вузов железнодорожного транспорта, а также силами специалистов локомотиворемонтных заводов и депо. Существуют различные направления в разработке методов диагностики тяговых электродвигателей, что объясняется разнообразием возможных неисправностей и типов дефектов ТЭД. В соответствии с правилами ремонта электрических двигателей техническое состояние паяного соединения считается удовлетворительным при степени пропайки контактного соединения не менее 80 % [5, 6], а превышение температуры является браковочным состоянием коллектора при оценке технического состояния якоря [9]. При некачественной пайке происходит увеличение переходного сопротивления в месте соединения и, как следствие, значительный нагрев, описываемый законом Джоуля – Ленца [3]. Для разработки методики диагностирования паяных соединений петушков коллектора возникает необходимость в создании и исследовании тепловой нестационарной модели коллектора ТЭД. Существуют различные методы расчета температурных полей двигателей постоянного тока, обладающие своими достоинствами и имеющие также свои недостатки, обусловленные допущениями, принятыми в математических моделях. Основные подходы к созданию математических моделей и выбору программной среды моделирования приведены в [2].

При анализе существующих методик тепловых расчетов был сформулирован вывод, что существующие методы определения температурного поля, не учитывающие геометрию коллектора, являются менее точными по сравнению с методом конечных элементов. Такие методы, как, например, метод тепловых схем замещения, имитирующий только пути передачи тепловых потоков, не дают полной картины теплограммы коллектора, а определяют лишь средние значения температуры отдельных элементов. При расчете теплового поля коллектора методом тепловых схем замещения используются выражения для расчета нагревания однородного тела, при этом коллектор в действительности не является однородным телом, так как в своем составе имеет не только медные коллекторные пластины, но и миканит, имеющий свою теплопроводность отличной от теплопроводности меди. Также возможно использование других композиционных материалов, теоретические основы создания и применения которых приведены в [7, 9]. Другими словами, коллектор тягового электродвигателя – это сложный объект исследования, требующий тщательного подхода к разработке его модели. Поэтому применение метода конечных элементов [1] в данном случае является более приемлемым при решении тепловых задач расчета теплограммы коллектора. Этот метод позволяет учитывать не только геометрию моделируемого тела, но и разнородность материалов и их разную теплопроводность, что в первую очередь сказывается на точности расчетов моделирования.

Согласно закону Джоуля – Ленца, нагрев в проводнике происходит от прохождения по нему электрического тока, и, как известно, изменение величины плотности тока влияет на величину тока, причем прямо пропорционально. Следовательно, тепловая модель коллектора электродвигателя должна быть связанной с моделью распределения плотности тока в коллекторной пластине. Поэтому с целью обнаружения наиболее нагреваемого места в коллекторе необходимо провести анализ распределения плотности тока в пластине электрической машины.

При построении модели по распределению плотности тока в коллекторной пластине ТЭД НБ-418 К6 преследовалась цель обнаружения наиболее нагреваемого места в коллекторе, что необходимо для получения более достоверной диагностической информации при выявлении такого типа дефекта, как «некачественная пайка в петушках коллектора электродвигателя». В ходе моделирования получена следующая модель, представленная на рис. 1.

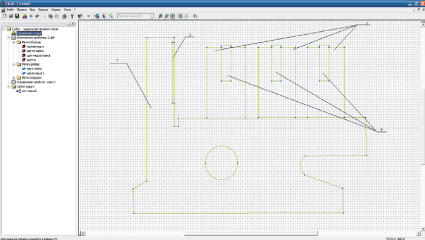
Рис. 1. Геометрия модели коллекторной пластины ТЭД НБ-418 К6 в программной среде Elcut

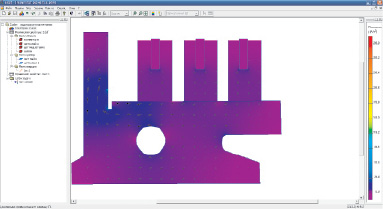
Рис. 2. Распределение плотности тока в коллекторной пластине ТЭД НБ-418 К6

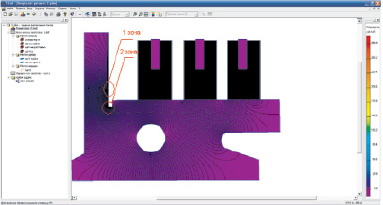
Рис. 3. Распределение плотности тока в зоне 1 и в зоне 2

На рис. 1 представлены следующие элементы: 1 – коллекторная пластина, 2 – место пайки в петушках коллектора электродвигателя, 3 – щетки двигателя, 4 – медные вставки (токопровод).

Результаты моделирования распределения плотности тока в коллекторной пластине представлены на рис. 2.

При расчете методом конечных элементов распределения плотности тока в пластине были получены следующие результаты, которые представлены на рис. 3–5.

По результатам моделирования выявлено, что большее распределение плотности тока происходит в двух условно обозначенных зонах. Это явление объясняется тем, что ток стремится пройти по кратчайшему пути (т.е. меньшее расстояние). А кратчайшему расстоянию для прохождения тока между системой «щетка – петушок – место пайки обмотки и петушка» как раз соответствуют условно обозначенные зоны (рис. 3). Таким образом, в результате моделирования были выявлены две основных зоны большего распределения плотности тока в месте соединения «петушок – обмотка» (выделенные красным цветом зоны и представленные на рис. 3). При еще более точном моделировании необходимо учитывать, что ток не распределяется равномерно по всей контактной поверхности щётки.

Причины этого весьма разнообразны, в частности:

– внешние факторы (пыль, газ, избыточная влажность, низкая температура);

– марка щётки не подходит к условиям работы машины (слишком толстый слой политуры, слишком большая или слишком малая плотность тока в щётках, вентиляция и т.д.).

При идентичном процессе ток может распределяться неравномерно между щётками на одном и том же щёткодержателе на коллекторе или на одной и той же траектории на кольце. Часто причиной этого может быть разное усилие нажатия, прикладываемое к щёткам. Все эти факторы можно учесть при моделировании, что сильно усложнит модель и увеличит время расчетов. Поэтому в модели не были учтены эти факторы.

При расчете модели по распределению плотности тока в зоне 1 и в зоне 2 для возможности анализа в этих зонах выделения тепла рассчитывается связанная модель тепловыделения в коллекторной пластине, представленная на рис. 4.

Первая зона имеет существенное значение для такого типа дефекта, как некачественная пайка, так как в ней расположено место пайки петушка и якорной обмотки. Следовательно, существенное влияние на дополнительный нагрев в этой зоне оказывает не только некачественная пайка «петушка» коллектора, но и распределение плотности тока в этой зоне. Результаты моделирования первой зоны представлены на рис. 5–6.

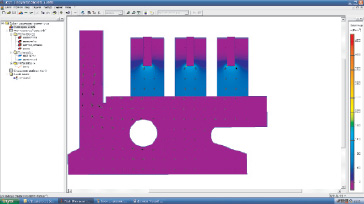
Рис. 4. Тепловыделение в системе «коллекторная пластина – щетки»

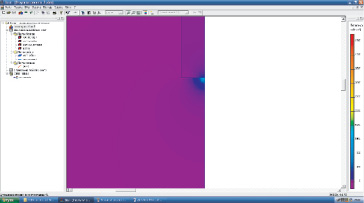
Рис. 5. Тепловыделение первой зоны «петушка» коллектора

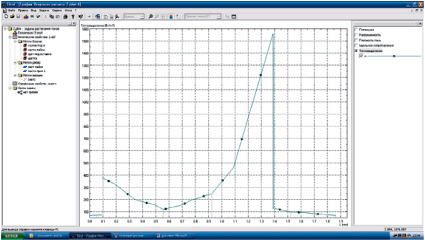
Рис. 6. Максимальное тепловыделение в первой зоне

Расчетные значения первой зоны

Из рис. 5–6 видно, что максимальное тепловыделение при качественной пайке в первой зоне составляет W = 496,717 Вт. Также из рисунка видно, что самое большое значение тепловыделения происходит еще под краем щетки W = 1550 Вт. Расчетные значения для первой зоны сводим в таблицу.

Выводы по результатам моделирования

1. При обосновании выбора источников выделения тепла учитываем факт неравномерного распределения плотности тока в коллекторной пластине, что видно из проведенного анализа и из рисунков, что особенно характерно для первой зоны, где имеет место распределение большего значения плотности тока, соответствующего большему нагреву в этом месте.

2. Большинство методик расчетов распределения тепла в коллекторе (например, метод тепловых схем замещения) не учитывают геометрию коллектора и являются менее точными по сравнению с методом конечных элементов.

3. Максимальное тепловыделение при качественной пайке составляет

W = 496,717 Вт.

4. С учетом вышеизложенного возникает необходимость в расчете модели с использованием метода конечных элементов в программной среде трехмерного моделирования с целью исследования влияния рассмотренного типа дефекта на нагрев коллектора.

Рецензенты:

Бабокин Г.И., д.т.н., профессор кафедры «Электрификация и энергоэффективность горных предприятий», Горный институт, ФГАОУ ВПО «Национальный исследовательский технологический университет «МИСиС», г. Москва;

Баландин О.А., д.т.н., заведующий кафедрой прикладной механики и инженерной графики, Забайкальский институт железнодорожного транспорта Иркутского государственного университета путей сообщения (ЗабИЖТ), г. Чита.

Работа поступила в редакцию 04.02.2015.

Библиографическая ссылка