Железобетонные арки, благодаря своей высокой несущей способности, находят широкое применение в строительстве. Так как в поперечных сечениях арки возникают два основных внутренних силовых фактора: изгибающий момент и продольная сила, то конструирование арок выполняют по общим правилам для внецентренно сжатых элементов.
Для железобетонных колонн, испытывающих внецентренное сжатие, имеются теоретические и экспериментальные данные о том, что вследствие ползучести бетона происходит перераспределение напряжений между арматурой и бетоном [1–6]. Аналогичное явление возможно и для арок. В настоящей статье рассматривается методика расчета железобетонных арок с учётом ползучести бетона методом конечных элементов. Расчётная схема, а также поперечное сечение арки показаны соответственно на рис. 1.
В качестве закона, описывающего связь между напряжениями и деформациями бетона, будем использовать уравнение вязкоупругой модели наследственного старения (ВУмНС) [1], которое имеет вид
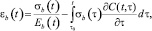 (1)
(1)
где εb(t) – деформация бетона; σb(t) – напряжение в бетоне; Eb(t) – модуль упругости бетона; C(t, τ) – мера ползучести, которая имеет вид
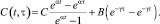 (2)
(2)
Перепишем уравнение (2) в виде
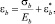 (3)
(3)
где 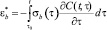 – деформация ползучести.
– деформация ползучести.
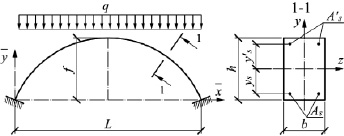
Рис. 1. Расчётная схема и поперечное сечение арки
Выразим в (3) напряжение через деформацию:
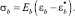 (4)
(4)
Полная деформация бетона представляет собой сумму осевой деформации 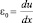 и деформации, обусловленной изменением кривизны:
и деформации, обусловленной изменением кривизны:
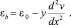 (5)
(5)
Деформации арматуры запишутся в виде
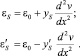 (6)
(6)
Потенциальная энергия деформации представляет собой сумму потенциальной энергии бетона и арматуры:
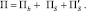 (7)
(7)
Потенциальная энергия бетона определяется следующим выражением
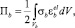 (8)
(8)
где 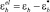 – упругая деформация бетона.
– упругая деформация бетона.
Подставив (4) и (5) в (8), получим:
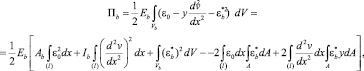 (9)
(9)
где 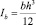 – момент инерции бетона; Ab = bh – площадь бетонного сечения.
– момент инерции бетона; Ab = bh – площадь бетонного сечения.
Потенциальная энергия деформации арматуры, расположенной у нижней грани, может быть найдена следующим образом:
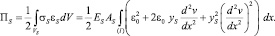 (10)
(10)
Аналогично для арматуры верхней грани:
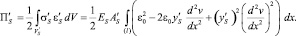 (11)
(11)
В случае симметричного армирования 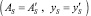 для потенциальной энергии деформации всей арматуры получим
для потенциальной энергии деформации всей арматуры получим
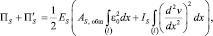 (12)
(12)
где 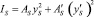 – момент инерции арматуры.
– момент инерции арматуры.
Для расчета будет использоваться стержневой конечный элемент, показанный на рис. 2. В каждом узле данного элемента имеется 3 степени свободы: 2 линейных перемещения u и v, а также угол поворота φ. Вектор узловых перемещений запишется в виде
{U} = {ui uj vi φi vj φj)}.
Прогиб конечного элемента будем аппроксимировать следующим образом:
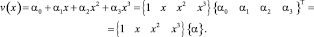 (13)
(13)
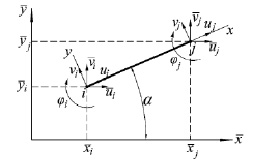
Рис. 2. Стержневой конечный элемент
Вектор {α} найдем из следующих условий:
v(0) = vi, 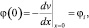 , v(l) = vj,
, v(l) = vj, 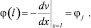
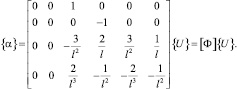 (14)
(14)
Вторая производная прогиба запишется в виде
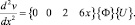 (15)
(15)
Для осевых перемещений u принимаем линейную зависимость от x:
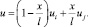 (16)
(16)
Тогда осевая деформация ε0 будет определяться следующим образом:
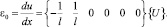 (17)
(17)
Подставив (15) и (17) в (9) и (12), получим следующее выражение для потенциальной энергии железобетонного элемента:
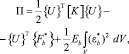 (18)
(18)
где 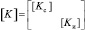 – матрица жесткости, которая имеет блочную структуру;
– матрица жесткости, которая имеет блочную структуру; 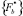 – вклад деформаций ползучести бетона в вектор узловых нагрузок;
– вклад деформаций ползучести бетона в вектор узловых нагрузок;

где 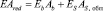 – жесткость приведенного сечения при центральном растяжении (сжатии);
– жесткость приведенного сечения при центральном растяжении (сжатии); 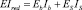 – жесткость приведенного сечения при изгибе.
– жесткость приведенного сечения при изгибе.
 (19)
(19)
Окончательно задача сводится к системе линейных алгебраических уравнений, имеющей вид
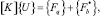 (20)
(20)
где {Fq} – вектор внешних узловых нагрузок.
Определение деформаций ползучести. В соответствии с выбранной реологической моделью деформация ползучести бетона определяется следующим образом:
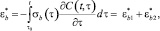 (21)
(21)
где 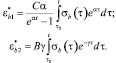
Найдем производную каждой составляющей по времени:
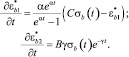 (22)
(22)
Методика решения задачи. Рассматриваемый временной интервал разбивается на n шагов Δt, а поперечное сечение каждого элемента по высоте на m частей Δy. На первом шаге выполняется решение упругой задачи 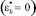 . По найденным перемещениям вычисляются напряжения, а по напряжениям находятся скорости роста составляющих
. По найденным перемещениям вычисляются напряжения, а по напряжениям находятся скорости роста составляющих 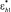 и
и 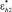 по формулам (22). Компоненты деформации ползучести в момент времени t + Δt определяются при помощи линейной аппроксимации.
по формулам (22). Компоненты деформации ползучести в момент времени t + Δt определяются при помощи линейной аппроксимации.
Была решена модельная задача при следующих исходных данных: пролет арки L = 16 м, подъем f = 3,2 м, b = 20 см, h = 40 см, τ0 = 28 сут, Eb(τ0) = 3∙104 МПа, реологические константы α = 0,032, γ = 0,062, C = 3,77∙10–5 МПа–1, B = 5,68∙10–5 МПа–1, коэффициент армирования 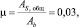
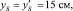 ES = 2∙105 МПа.
ES = 2∙105 МПа.
Рис. 3 – изменение напряжений в бетоне в середине пролёта. Рис. 4–5 – соответственно графики изменения напряжений в арматуре у верхней и нижней грани.
Из рис. 3–5 видно, что вследствие ползучести бетона происходит перераспределение напряжений: в бетоне напряжения по абсолютному значению снижаются, а в арматуре возрастают. У верхней грани наиболее существенно меняются напряжения в середине пролета: в арматуре сжимающие напряжения 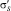 возрастают с 52,48 до 97,46 МПа, а в бетоне убывают с 8,27 до 6,84 МПа.
возрастают с 52,48 до 97,46 МПа, а в бетоне убывают с 8,27 до 6,84 МПа.
У нижней грани наиболее значительное перераспределение происходит в сечениях x = 0 и x = l: в арматуре сжимающие напряжения σS возрастают с 70,7 до 131,4 МПа, а в бетоне убывают с 11,3 до 9,35 МПа.
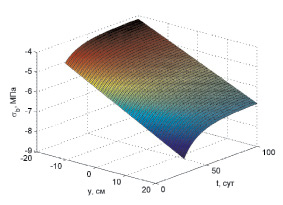
Рис. 3. Изменение напряжений в бетоне по высоте сечения при 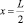
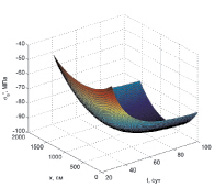
Рис. 4. Изменение напряжений в арматуре у верхней грани
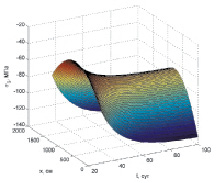
Рис. 5. Изменение напряжений в арматуре у нижней грани
Таким образом, даже линейная ползучесть бетона оказывает существенное влияние на напряженно-деформированное состояние железобетонных арок. В рассмотренном примере напряжения в арматуре у верхней грани в середине пролета возросли в 1,85 раз.
Рецензенты:
Бескопыльный А.Н., д.т.н., профессор кафедры технической эксплуатации и сервиса автомобилей и оборудования, проректор по учебной работе, Ростовский государственный строительный университет, г. Ростов-на-Дону;
Маилян Д.Р., д.т.н., профессор, заведующий кафедрой «Железобетонные и каменные конструкции», ФГБОУ ВПО «Ростовский государственный строительный университет», г. Ростов-на-Дону.
Работа поступила в редакцию 04.02.2015.
Библиографическая ссылка
Аваков А.А., Чепурненко А.С., Литвинов С.В. НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ЖЕЛЕЗОБЕТОННОЙ АРКИ С УЧЕТОМ ПОЛЗУЧЕСТИ БЕТОНА // Фундаментальные исследования. 2015. № 3. С. 9-14;URL: https://fundamental-research.ru/ru/article/view?id=37075 (дата обращения: 07.02.2026).



