Проблемы разработки систем менеджмента качества (СМК) высшей школы в последние годы приобрели общепризнанную актуальность и являются основной движущей силой реформы системы высшего образования в России [1]. Существует несколько подходов, позволяющих построить систему менеджмента качества вуза. Одним из них является принцип Всеобщего менеджмента качества (Total Quality Management - TQM). Принципами TQM являются ориентация на потребителей образовательных услуг, системный подход к менеджменту образовательного процесса, подход к управлению как к процессу, вовлечение сотрудников в процессы менеджмента и постоянное улучшение системы качества. Согласно TQM, для достижения реальной эффективности принимаемых решений в системе менеджмента качества предоставления образовательных услуг необходимо добиться закрепления принципа принятия решений, базирующегося на анализе данных и информации, исключая волюнтаризм и авторитарность [2]. В том числе, проблемой, решение которой непосредственно влияет на качество образования, является принятие решений о распределении нагрузки между преподавателями.
Исследуем организацию учебного процесса в ВУЗе. Преподаватели преподают дисциплины студентам. По каждой дисциплине студенты должны пройти курс, на который в учебном плане отводится некоторое количество часов. Эти учебные часы составляют нагрузку преподавателей. Пусть на кафедре работают несколько преподавателей, некоторые из них могут вести несколько предметов, некоторые - только один.
Цель работы - распределить нагрузку между преподавателями оптимальным в некотором смысле образом. Для достижения цели необходимо решить ряд задач:
- сформировать разумный критерий качества распределения нагрузки;
- выбрать метод принятия решения;
- опробовать выбранный метод на тестовом примере.
Примем за критерий распределения нагрузки компетентность преподавателя в конкретной дисциплине. Компетентность представим комплексным критерием, учитывающим ряд факторов, которые поддаются непосредственному вычислению.
В качестве примера решим такую задачу: студенты направления «Информатика и вычислительная техника» изучают такие дисциплины, как «Информатика», «Операционные системы и среды», «Базы данных», «Информационные технологии», «Системное ПО», «Теория принятия решения», «САПР».
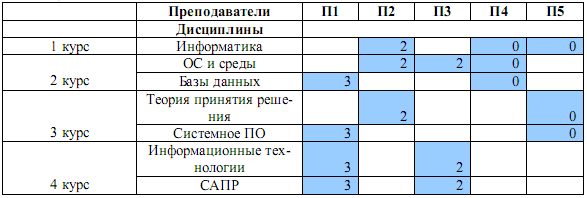
Допустим, что компетенция преподавателей ограничена и соответствует таблице 1, где закрашенная клетка означает, что преподаватель в принципе может вести дисциплину.
Так, преподаватель П1 может вести дисциплины «Базы данных», «Системное ПО», «Информационные технологии» и «САПР».
Таблица 1. Компетентность преподавателей

Решение задачи оптимального распределения нагрузки сведем к решению задачи о распределении ресурсов [3]. Составим целевую функцию:
![]() → MAX, (1)
→ MAX, (1)
где ![]() - количество часов, отведенных на i-дисциплину.
- количество часов, отведенных на i-дисциплину.
Примем, что коэффициент, учитывающий компетентность j-го преподавателя в i-ой дисциплине Cij рассчитывается по формуле:
![]() , (2)
, (2)
где ![]() - коэффициент, учитывающий стаж преподавания i-ой дисциплины j-ым преподавателем;
- коэффициент, учитывающий стаж преподавания i-ой дисциплины j-ым преподавателем;
Mij- коэффициент, учитывающий методические разработки j-го преподавателя по i-ой дисциплине;
![]() - коэффициент, учитывающий результаты итогового тестирования по i-ой дисциплине;
- коэффициент, учитывающий результаты итогового тестирования по i-ой дисциплине;
![]() - коэффициент, учитывающий ученую степень j-го преподавателя;
- коэффициент, учитывающий ученую степень j-го преподавателя;
![]() - коэффициент, учитывающий предпочтение j-го преподавателя вести i-ую дисциплину.
- коэффициент, учитывающий предпочтение j-го преподавателя вести i-ую дисциплину.
Для расчета этих коэффициентов предлагаются следующие формулы, основанные на здравом смысле и доступной информации о ходе учебного процесса. Весовые коэффициенты ![]() предположим равными 1, так как их обоснованный выбор выходит за цели настоящей работы и является предметом экспертной оценки сравнительной важности параметров.
предположим равными 1, так как их обоснованный выбор выходит за цели настоящей работы и является предметом экспертной оценки сравнительной важности параметров.
Расчет коэффициента Zij, учитывающего стаж j-го преподавателя по i-ой дисциплине произведем по формуле:
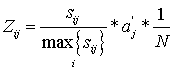 , (3)
, (3)
где N - количество конкурентов на преподавание -ой дисциплины,
Sij - стаж преподавания j-го преподавателя i-ой дисциплины,
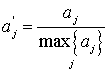 - нормированный относительно максимального значения aj стаж,
- нормированный относительно максимального значения aj стаж,
aj- общий стаж преподавания j-го преподавателя. Так как преподаватель одновременно может вести сразу несколько дисциплин, то ![]()
Предположим, что преподаватели имеют следующие стажи преподавания Sij (табл. 2).
Таблица 2.
|
|
|
|
|
|
|
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
Дисциплины |
|
|||||
|
1 курс |
Информатика |
|
12 |
|
5 |
4 |
|
2 курс |
ОС и среды |
|
9 |
15 |
2 |
|
|
Базы данных |
20 |
|
|
1 |
|
|
|
3 курс |
Теория принятия решения |
|
9 |
|
|
4 |
|
Системное ПО |
10 |
|
|
|
2 |
|
|
4 курс |
Информационные технологии |
8 |
|
13 |
|
|
|
САПР |
9 |
|
5 |
|
|
|
|
|
Общий стаж работы aj |
30 |
14 |
20 |
5 |
7 |
Из таблицы 2 видно, что общий стаж преподавания преподавателя П1 - 30 лет. Из этих тридцати лет преподаватель П1 20 лет преподает базы данных, 10 лет - системное ПО, 8 лет - информационные технологии и 9 лет - САПР. В нашем примере максимальный стаж имеет преподаватель П1, поэтому 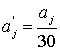 . Получим следующие значения
. Получим следующие значения ![]() (табл. 3):
(табл. 3):
Таблица 3.
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
Нормированный стаж |
1 |
0,467 |
0,667 |
0,167 |
0,233 |
Подставим значения в формулу 3, получим следующие коэффициенты Zij (табл. 4).
Расчет коэффициента Mij, учитывающего количество методических пособий, разработанных j-ым преподавателем по i-ой дисциплине произведем по формуле
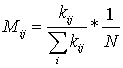 , (4)
, (4)
где N - количество «конкурентов»;
kij - количество методических пособий, разработанных j-ым преподавателем по i-ой дисциплине. Будем учитывать именно количество методических пособий безотносительно их объема, поскольку сложно предположить обоснованную методику учета объема пособий.
Таблица 4.
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
|
Дисциплины |
|
|||||
|
1 курс |
Информатика |
|
0,156 |
|
0,023 |
0,026 |
|
|
2 курс |
ОС и среды |
|
0,093 |
0,222 |
0,007 |
|
|
|
Базы данных |
0,5 |
|
|
0,004 |
|
||
|
3 курс |
Теория принятия решения |
|
0,234 |
|
|
0,052 |
|
|
Системное ПО |
0,5 |
|
|
|
0,023 |
||
|
4 курс |
Информационные технологии |
0,308 |
|
0,334 |
|
|
|
|
САПР |
0,5 |
|
0,186 |
|
|
||
|
|
Нормированный стаж |
1 |
0,467 |
0,667 |
0,167 |
0,233 |
|
Предположим, что преподавателями за все время работы разработано следующее количество kij учебных пособий (табл. 5)
Таблица 5.
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
Дисциплины |
|
||||
|
1 курс |
Информатика |
|
5 |
|
1 |
2 |
|
2 курс |
ОС и среды |
|
6 |
4 |
1 |
|
|
Базы данных |
9 |
|
|
0 |
|
|
|
3 курс |
Теория принятия решения |
|
4 |
|
|
2 |
|
Системное ПО |
3 |
|
|
|
0 |
|
|
4 курс |
Информационные технологии |
5 |
|
10 |
|
|
|
САПР |
8 |
|
2 |
|
|
|
Применив формулу 4, получим следующие коэффициенты Mij (табл.6):
Таблица 6.
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
Дисциплины |
|
||||
|
1 курс |
информатика |
|
0,208 |
|
0,042 |
0,083 |
|
2 курс |
ОС и среды |
|
0,182 |
0,121 |
0,031 |
|
|
Базы данных |
0,5 |
|
|
0 |
|
|
|
3 курс |
Теория принятия решения |
|
0,334 |
|
|
0,167 |
|
Системное ПО |
0,5 |
|
|
|
0 |
|
|
4 курс |
Информационные технологии |
0,167 |
|
0,334 |
|
|
|
САПР |
0,4 |
|
0,1 |
|
|
|
Совершенствование контроля качества образования является одним из важнейших направлений реформирования системы российского образования. В настоящее время в России одновременно с существующей традиционной системой оценки и контроля результатов обучения складывается новая система, основанная на использовании тестовых технологий. Это вызвано потребностью в получении независимой объективной информации о результатах деятельности образовательных учреждений: проверка знаний, умений и навыков студентов, компетентности преподавателя, оценки качества образования. [4]
Пусть после изучения некоторой дисциплины у i-го преподавателя студенты проходят итоговое тестирование по этому предмету. Причем тестовые задания составляются независимыми тестологами, а за ходом тестирования следит комиссия проверяющих, в которую не входит данный преподаватель. Рассчитаем коэффициент ![]() по результатам этого тестирования.
по результатам этого тестирования.
Назначим следующие весовые коэффициенты ![]() оценок, полученных в результате тестирования:
оценок, полученных в результате тестирования:
«5»: ![]()
«4»: ![]()
«3»: ![]()
«2»: ![]()
Выбор весовых коэффициентов основывается на следующем:
- оценка знаний «5» требует отличного знания предмета, поэтому вес оценки очень высок по сравнению с другими оценками (0,45);
- оценка «4» означает, что студент довольно хорошо (но не на 100%) ориентируется в данной дисциплине. Вес меньше, чем вес оценки «5», но все-таки достаточно высок (0,35);
- оценка «3» - знания в данной области посредственные. Вес оценки «3» незначительный (0,2);
- оценка «2» - знание предмета неудовлетворительное. За такое качество знаний вес не назначается (0).
В сумме вес оценок ![]() , то есть их можно рассматривать как нормированные весовые коэффициенты полученных оценок.
, то есть их можно рассматривать как нормированные весовые коэффициенты полученных оценок.
Расчет коэффициента ![]() , учитывающего результаты итогового тестирования по i-ой дисциплине проведем по формуле
, учитывающего результаты итогового тестирования по i-ой дисциплине проведем по формуле
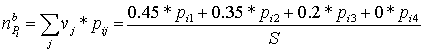 (5),
(5),
где S - количество студентов, сдававших экзамены по i-ой дисциплине;
b - дисциплина;
pij - количество студентов, получивших j-ую оценку.
Очевидно, что при принятых значениях весов оценок коэффициент ![]() .
.
Зададимся разумными результатами тестирования. Рассчитаем коэффициенты по формуле 5. Получим следующие значения коэффициентов ![]() (табл. 7):
(табл. 7):
Таблица 7.
|
Информатика |
pi1 |
pi2 |
pi3 |
pi4 |
|
|
|
5 |
4 |
3 |
2 |
nинфпi |
|
П2 |
10 |
17 |
9 |
4 |
0,306 |
|
П4 |
16 |
7 |
9 |
8 |
0,286 |
|
П5 |
13 |
15 |
2 |
10 |
0,288 |
|
Операционные системы |
pi1 |
pi2 |
pi3 |
pi4 |
nоспi |
|
|
5 |
4 |
3 |
2 |
|
|
П2 |
11 |
12 |
9 |
8 |
0,274 |
|
П3 |
15 |
8 |
7 |
10 |
0,274 |
|
П4 |
8 |
14 |
13 |
5 |
0,278 |
|
Базы данных |
pi1 |
pi2 |
pi3 |
pi4 |
nбдпi |
|
|
5 |
4 |
3 |
2 |
|
|
П1 |
9 |
15 |
10 |
6 |
0,283 |
|
П4 |
8 |
10 |
11 |
11 |
0,233 |
|
Теория принятия решений |
pi1 |
pi2 |
pi3 |
pi4 |
nтпрпi |
|
|
5 |
4 |
3 |
2 |
|
|
П2 |
14 |
8 |
9 |
9 |
0,273 |
|
П5 |
7 |
10 |
10 |
13 |
0,216 |
|
Системное ПО |
pi1 |
pi2 |
pi3 |
pi4 |
nспопi |
|
|
5 |
4 |
3 |
2 |
|
|
П1 |
8 |
19 |
12 |
1 |
0,316 |
|
П5 |
11 |
7 |
12 |
10 |
0,245 |
|
Информационные технологии |
pi1 |
pi2 |
pi3 |
pi4 |
nитпi |
|
|
5 |
4 |
3 |
2 |
|
|
П1 |
4 |
18 |
10 |
8 |
0,253 |
|
П3 |
12 |
17 |
8 |
3 |
0,324 |
|
САПР |
pi1 |
pi2 |
pi3 |
pi4 |
nсапрпi |
|
|
5 |
4 |
3 |
2 |
|
|
П1 |
12 |
5 |
20 |
3 |
0,279 |
|
П3 |
14 |
3 |
18 |
5 |
0,274 |
Сведем полученные коэффициенты ![]() в одну (табл. 8):
в одну (табл. 8):
Таблица 8.
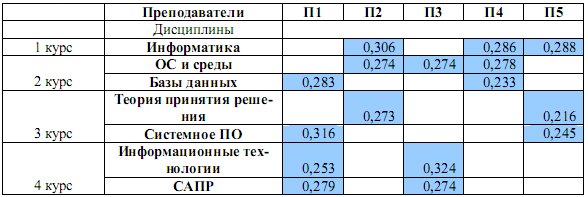
Основываясь на результатах, приведенных в таблице 8, можно сделать вывод, что, например, студенты, изучавшие дисциплину «Информатика» у преподавателя П2, знают ее лучше, чем студенты, изучавшие информатику у преподавателей П4 и П5; а преподаватели П2 и П3 обеспечивают одинаковый уровень знаний студентов по дисциплине «Операционные системы и среды», так как соответствующие коэффициенты равны.
Исходя из требований к лицензированию вуза, доля преподавателей с учеными степенями докторов наук и учеными званиями профессоров, привлекаемых к образовательному процессу, должна быть не менее 10%, а общий процент профессорско-преподавательского состава, имеющих ученую степень кандидата или доктора наук, должен быть не менее 67% [5]. Поэтому при расчете коэффициента компетентности преподавателя Cij - немаловажную роль играет его ученая степень.
В Российской Федерации существуют ученые степени кандидата наук и доктора наук. Примем за весовые коэффициенты uj, учитывающие ученую степень j-го преподавателя:
- Кандидат наук
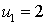 .
. - Доктор наук
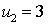 .
.
Допустим, в нашем примере степень кандидата наук имеют преподаватели П2 и П3, а ученую степень доктора наук - преподаватель П4. Составим таблицу коэффициентов uj (табл. 9).
Таблица 9.
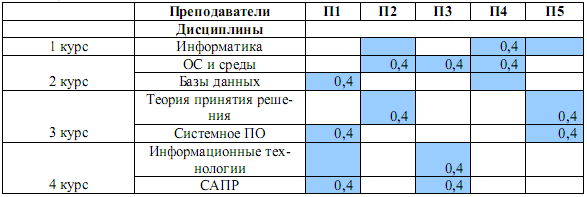
За желание вести i-ую дисциплину добавим соответствующему j-му преподавателю wij = 0,4 балла. Это разумно, поскольку нерационально назначать нагрузку преподавателю, который не склонен вести конкретную дисциплину.
Предположим, что желания профессорско-преподавательского состава wij разделились следующим образом (табл. 10):
Таблица 10.
По формуле 2 получим матрицу Cij сложением матриц коэффициентов, приведенных в таблицах 4, 6, 8, 9 и 10 (табл. 11). Очевидно, что, в случае, если преподаватель не компетентен в преподавании дисциплины (см. табл. 1), Cij ≡ 0
Таблица 11.
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
Дисциплины |
|
|
|
|
|
|
1 курс |
Информатика |
0 |
4,382 |
0 |
1,006 |
0,682 |
|
2 курс |
ОС и среды |
0 |
4,257 |
6,13 |
0,821 |
0 |
|
Базы данных |
14,183 |
0 |
0 |
0,317 |
0 |
|
|
3 курс |
Теория принятия решения |
0 |
5,109 |
0 |
0 |
1,249 |
|
Системное ПО |
9,216 |
0 |
0 |
0 |
0,878 |
|
|
4 курс |
Информационные технологии |
7,42 |
0 |
7,393 |
0 |
0 |
|
САПР |
8,579 |
0 |
4,441 |
0 |
0 |
Для формализации ограничений составим табл.12, содержащую решение нашей задачи, где xij - количество часов, отведенных на i-ую дисциплину j-му преподавателю.
Таблица 12.
|
|
Преподаватели |
П1 |
П2 |
П3 |
П4 |
П5 |
|
|
Дисциплины |
|
|
|
|
|
|
1 курс |
Информатика |
x11 |
x12 |
x13 |
x14 |
x15 |
|
2 курс |
ОС и среды |
x21 |
x22 |
x23 |
x24 |
x25 |
|
Базы данных |
x31 |
x32 |
x33 |
x34 |
x35 |
|
|
3 курс |
Теория принятия решения |
x41 |
x42 |
x43 |
x44 |
x45 |
|
Системное ПО |
x51 |
x52 |
x53 |
x54 |
x55 |
|
|
4 курс |
Информационные технологии |
x61 |
x62 |
x63 |
x64 |
x65 |
|
САПР |
x71 |
x72 |
x73 |
x74 |
x75 |
Введем ограничения на распределение нагрузки:
1. j -му преподавателю нельзя вести i-ую дисциплину, если он в ней совершенно некомпетентен, поэтому введем требование ![]() .
.
2. Нагрузка должна быть равномерно распределена между преподавателями. Например, коэффициент компетентности преподавателя П1 гораздо выше коэффициента компетентности любого другого преподавателя, так как у него самый большой стаж работы, большое количество методических пособий, есть ученая степень и т.д. Но «отдать» ему вести все дисциплины нельзя, иначе менее компетентные преподаватели останутся без нагрузки, а преподаватель П1 будет перегружен. Пусть на каждую дисциплину отведено 140 часов. Введем ограничение на нагрузку: максимальная нагрузка преподавателя в семестре не должна превосходить XMAX =280 часов (т.е. преподаватель не может вести в одном семестре более двух дисциплин). Однако может случиться так, что молодые преподаватели не получат часов для нагрузки (так как большую роль в расчете играет коэффициент компетентности, куда входит и стаж, и степень, и разработанные преподавателем методические пособия). Поэтому введем ограничение и на минимальную нагрузку: нагрузка преподавателя должна быть не менее XMIN =140 часов в семестр.
Получим следующие ограничения:
a) 140 <= х31 + х51 + х61 + х71 <= 280 (для преподавателя П1);
b) 140 <= x12 + x22 + x42 <= 280 (для П2);
c) 140 <= x23 + x63 + x73 <= 280 (для П3);
d) 140 <= x14 + x24 + x34 <= 280 (для П4);
e) 140 <= x15 + x45 + x55 <=280 (для П5).
3. Преподаватель не должен вести больше одной дисциплины у одной группы одновременно. Это не строгое и, возможно, спорное ограничение, но оно обусловлено тем, что кругозор студентов с большей долей вероятности может расшириться при общении с большим количеством преподавателей. Введем следующие ограничения:
a) x24 + x34 <= 140 (преподаватель П4 может преподавать группе 2 курса и операционные системы и базы данных, не дадим ему такой возможности);
b) x45 + x55 <= 140 (преподаватель П5 может преподавать группе 3 курса и теорию принятия решений, и системное ПО);
c) x61 + x71 <= 140 (преподаватель П1 может преподавать группе 4 курса и информационные технологии и САПР);
d) x63 + x73 <= 140 (преподаватель П3 может преподавать группе 4 курса информационные технологии и САПР).
Найдем решение задачи при помощи надстройки «Поиск решения» Microsoft Excel, ставя задачу максимизации целевого параметра (1). Результат представлен в табл. 13.
Таблица 13.
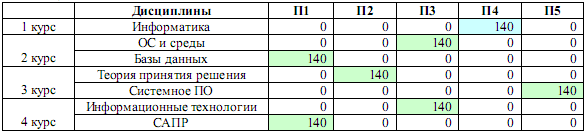
Получили следующее распределение нагрузки (таблица 12):
- Преподаватель П1 будет вести базы данных у группы 2 курса и САПР у группы 4 курса.
- Преподаватель П2 - теорию принятия решений у 3 курса.
- Преподаватель П3 - операционные системы и среды (2 курс) и информационные технологии (4 курс).
- Преподаватель П4 - информатику (1 курс).
- Преподаватель П5 - системное программное обеспечение у группы 3 курса.
Проверка решения, приведенного в табл. 13, подтверждает, что соблюдаются все ограничения. Нагрузка распределена равномерно.
Вывод: построена модель, позволяющая распределить нагрузку между преподавателями, определены ограничения, приняты допущения, выбран метод поиска и решен тестовый пример. Актуальность и практическая значимость работы определяется тем, что российская система образования сейчас находится в процессе реформирования, повышаются контроль и требования к качеству образования. Добиться повышения качества можно, в том числе, рациональным распределением нагрузки между преподавателями путем интеграции разработанной модели в информационно-управляющую систему ВУЗа или кафедры.
СПИСОК ЛИТЕРАТУРЫ:
- Варламова С.А. Эффективное представление информации для обеспечения деятельности филиала ВУЗа / С.А. Варламова, А.В. Затонский // Математические методы в технике и технологиях: Материалы 20-й Международ. науч. конф., Т.9- Ярославль, 2007.- С.220-226
- Затонский А.В. Информационная система обеспечения качества образования в вузе / А.В. Затонский, Н.С. Калинина // Математические методы в технике и технологиях: Материалы 19-й Международ. науч. конф., Т.4. Воронеж, 2006, С.173-177
- Орлов А.И. Теория принятия решений: учебник. - М.: Экзамен, 2006. - 574 с.
- Ковалева Г.С., Сацевич С.В., Татур А.О., Челышкова М.Б., Шмелев А.Г. Федеральная система тестирования. Проект концепции. Газета. Первое сентября N 11-2000
- Геворкян Е.Н. Временные требования, предъявляемые к образовательным учреждениям среднего, высшего и дополнительного профессионального образования при проведении лицензионной экспертизы и проверки их готовности к реализации образовательных программ.
- Положение «О государственной аккредитации высшего учебного заведения» (в редакции Постановления Правительства РФ от 01.02.2005 N49)
Библиографическая ссылка
Варламова С.А., Белобородова Е.В., Затонский А.В. ПРИНЯТИЕ РЕШЕНИЙ ПРИ РАСПРЕДЕЛЕНИИ УЧЕБНОЙ НАГРУЗКИ // Фундаментальные исследования. 2008. № 9. С. 22-31;URL: https://fundamental-research.ru/ru/article/view?id=3697 (дата обращения: 12.03.2026).



