Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Багаутдинов И.Н. 1 Журавлев Е.А. 1 Богданов Е.Н. 1

---

1 ФГБОУ ВПО «Поволжский государственный технологический университет»

Описано взаимодействие звеньев механизма? связанных вращательной кинематической парой? и элементов гидравлического двигателя поступательного движения. Получены выражения для приводной обобщенной силы, отнесенной к углу взаимного поворота звеньев и для передаточных функций, связывающих перемещение и скорость штока гидроцилиндра c углом и угловой скоростью относительного поворота звеньев. Векторно-матричная форма этих выражений облегчает их использование в алгоритмах автоматического формирования уравнений динамики многозвенных механизмов. В математической модели гидравлической части привода использованы уравнения баланса расходов рабочей жидкости с учетом её объемного сжатия, которые дают по одному дифференциальному уравнению первого порядка для каждой полости двигателя. Представлены результаты численной реализации предлагаемого описания для плоского трехзвенного механизма, приводимого в движение тремя гидроцилиндрами с дроссельным программным управлением.

Статья в формате PDF

973 KB

гидропривод

вращательная пара

обобщенная приводная сила

динамика многозвенного механизма

численное решение

1. Багаутдинов И.Н., Шестаков Я.И. Оценка влияния неплоскостности опорного кольца опорно-поворотного круга платформы машины ЛП-19В на напряженное состояние механизма поворота // Известия вузов. Лесной журнал. – 2002. – № 7. – С. 38–44.

2. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. – М.: Машиностроение, 1976. – 424 с.

3. Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы: динамика, управление, оптимизация. – М.: Наука, 1989. – 368 с.

4. Luh J. Y.S., Walker M.W., Paul R.P.C. On-line computational scheme for mechanical manipulators // Trans. ASME, J. of Dynamic Systems, Measurement & Control. – Vol. 102. – 1980. – Р. 69–76.

5. Walker M.W., Orin D.E., Efficient dynamic computer simulation of robotic mechanisms, Trans. ASME // J. of Dynamic Systems, Measurement & Control. – Vol. 104. – 1982. – Р. 205–211.

Гидравлические двигатели поступательного действия – гидроцилиндры ‒ находят широкое применение в шарнирно ‒ рычажных исполнительных механизмах для обеспечения взаимного поворота звеньев [1]. Если силовой электропривод имеет достаточно простую математическую модель, которая легко встраивается в известные способы описания динамики манипуляционных механизмов [3], то для гидравлического привода многозвенных шарнирных механизмов унифицированное описание кинематики и динамики в современной технической литературе отсутствует. Создание такого описания является целью настоящей работы.

При построении гидравлической части математической модели привода используются обычные допущения технической гидравлики и известные уравнения [2], описывающие динамику элементов привода – распределителей, трубопроводов, гидроцилиндров.

Математическая модель

Рассматривается механизм, состоящий из n жестких звеньев, последовательно связанных вращательными парами; первое звено связано вращательной парой с неподвижным основанием. Механизм приводится в движение гидравлическими двигателями G₁ , G₂, ..., G_n. Каждый двигатель - одноштоковый гидроцилиндр, управляющий взаимным поворотом двух смежных звеньев. В соответствии с конструкторской практикой полагаем шток k-го двигателя шарнирно связанным с k-м звеном, а его цилиндр - с (k - 1)-м звеном (рис. 1).

С каждым k-м звеном жестко свяжем правую ортогональную систему координат О_kX_kY_kZ_k, ось О_kZ_k которой совпадает с осью шарнира, соединяющего k-е и (k - 1)-е звенья (рис. 1). С неподвижным основанием механизма связана базовая система координат О₀X₀Y₀Z₀. Положение каждого k-го звена относительно (k - 1)-го определяется величиной q_k угла его поворота (по ходу часовой стрелки) вокруг оси О_kZ_k, до положения в котором ось О_kX_k становится параллельной плоскости О_k-1X_k-1Z_k-1. В том случае, когда оси О_k-1Z_k-1 и О_kZ_k параллельны, за q_k принимается величина угла поворота k-го звена до совпадения направлений осей О_kX_k и О_k-1X_k-1. В результате конфигурация механизма полностью определяется набором обобщенных координат q, q₂, ..., q_n.

Матрицу линейного преобразования координат трехмерного вектора из системы координат О_k-1X_k-1Y_k-1Z_k-1 в систему координат О_kX_kY_kZ_k обозначим T_k(q_k).

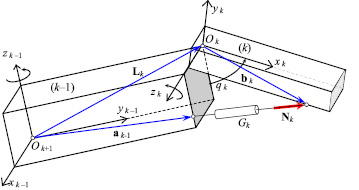
Рис. 1. Схема шарнирного сочленения смежных звеньев механизма

Введем следующие обозначения:

L_k-1 - радиус-вектор точки О_k относительно центра О_k-1; а_k-1 - радиус-вектор центра шарнирного соединения цилиндра двигателя G_k со звеном k - 1 относительно центра О_k-1; b_k - радиус-вектор центра шарнирного соединения штока двигателя G_k со звеном k относительно центра О_k.

Вектор N_k силы, действующей на k-е звено со стороны штока гидроцилиндра G_k, представим в виде

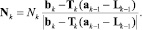(1)

Здесь N_k – алгебраическая величина силы, которая имеет положительный знак, если вектор N_k направлен от (k – 1)-го к k-му звену. Естественно задавать векторы b_k и а_k–1, L_k–1 в (1) их постоянными координатами в соответствующих локальных системах координат.

Очевидно, что обобщенная приводная сила Q_k, соответствующая координате qk равна моменту силы N_k относительно оси О_kZ_k и может быть представлена в виде

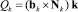
где k – орт оси О_kZ_k.

C учетом (1) это выражение принимает следующий вид:

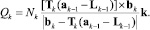(2)

Величина силы Nk определяется разностью давлений в полостях двигателя Gk:

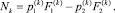(3)

где 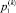, 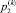– давления рабочей жидкости в полостях гидроцилиндра Gk; 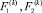– соответствующие рабочие площади поршня. Повсюду в дальнейшем нижний индекс 1 указывает на принадлежность величины к поршневой полости двигателя, а нижний индекс 2 – к штоковой полости.

Управление работой гидравлического двигателя осуществляется при помощи гидравлического распределителя (дросселя), который обеспечивает подключение рабочей полости двигателя к напорной магистрали, а сливной полости – к сливной магистрали.

При описании работы гидравлического двигателя использовались следующие предположения:

1) давления в напорной и сливной магистралях каждого двигателя постоянны и равны p_н и p_с соответственно;

2) гидравлическими потерями, связанными с утечками рабочей жидкости, можно пренебречь;

3) деформация трубопроводов, вызванная изменением давления рабочей жидкости, пренебрежимо мала;

4) падение давления рабочей жидкости вдоль участков трубопроводов, соединяющих распределитель и полости двигателя, не учитывается;

5) силы сухого и вязкого трения поршней о стенки цилиндров пренебрежимо малы по сравнению с приводными силами Nk .

Для установления зависимостей давлений 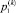, 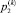в полостях двигателя G_k от перемещения s_k его штока были использованы дифференциальные уравнения работы [2], которые выражают условия баланса расходов рабочей жидкости, поступающей от распределителя в полости гидроцилиндра с учетом её объемного сжатия. В том случае, когда рабочей является поршневая полость двигателя, эти уравнения, с учетом принятых выше допущений, приобретают следующий вид:

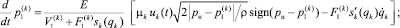
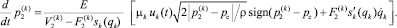(4)

Здесь E и ρ – модуль объемного сжатия и плотность рабочей жидкости; 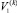, 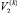– объемы полостей двигателя вместе с участками трубопровода, соединяющих полость с распределителем при среднем положении поршня; μ_k – безразмерный коэффициент окна распределителя (0 < μ_k ≤ 1); u_k(t) – регулируемая площадь проходного сечения окна распределителя; s_k(q_k) – перемещение штока двигателя, выраженное через обобщенную координату q_k; 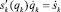– скорость штока, выраженная через обобщенную скорость 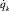. Для перемещения s_k за положительное принимается направление к звену с номером k.

В том случае, когда рабочей является штоковая полость, уравнения (4) принимают следующий вид:

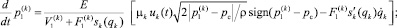
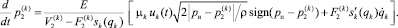(5)

Используя введенные ранее векторы b_k, L_k–1, а_k–1 и матрицы T_k(q_k), получим матричные выражения для кинематических передаточных функций s_k(q_k), 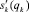, входящих в (4) и (5):

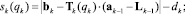
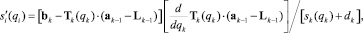(6)

где d_k – расстояние между центрами опорных шарниров двигателя G_k при среднем положении штока.

Добавляя к соотношениям (2), (3), (4), (5) дифференциальные уравнения динамики [4] рассматриваемого n-звенного механизма

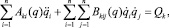k = 1, …, n, (7)

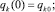
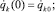
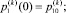
а также начальные условия 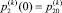и программу изменения управляющих переменных – площадей проходных сечений окон распределителей u_k = u_k(t), t ≥ 0, получаем замкнутую систему уравнений описывающих движение механизма с гидравлическим приводом, имеющим программное дроссельное управление.

Численная реализация математической модели

В качестве примера использования предлагаемой модели выполнен расчет движения плоского трехзвенного механизма с тремя гидравлическими двигателями. Схема механизма, расположение локальных систем координат и двигателей показано на рис. 2.

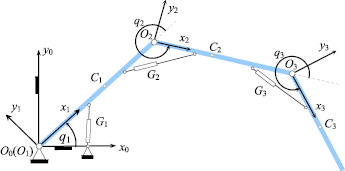
Рис. 2. Схема плоского трехзвенного исполнительного механизма

Геометрические параметры механизма: Lk = 0,8 м,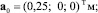

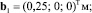
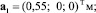
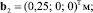
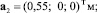
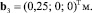
Массы звеньев m_k = 6 кг; локальные координаты их центров масс 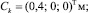главные центральные моменты инерции звеньев I_k = 0,32 кг∙м2. Массы гидравлических двигателей считались пренебрежимо малыми.

Система дифференциальных уравнений динамики (7) для плоского шарнирного трехзвенного механизма была получена средствами компьютерной алгебры пакета Maple 4 на основе модифицированного рекурсивного алгоритма Ньютона ‒ Эйлера, описанного в работе [5].

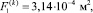
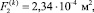
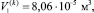
Параметры гидропривода: p_н = 1,5 МПа, pс = 100 кПа, 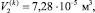μ_k = 0,7, d_k = 0,395 м.

Характеристики рабочей жидкости: ρ = 800 кг/м3, E = 1300 МПа.

Рассматривается движение механизма в горизонтальной плоскости при начальных условиях: q₁(0) = 1,396 рад; q₂(0) = –0,524 рад; q₃(0) = –1,222 рад; 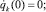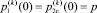, (k = 1, 2, 3).

Рабочая жидкость подается в поршневую полость двигателя G₁ и в штоковые полости двигателей G₂, G₃. Программы управления для всех распределителей одинаковы:

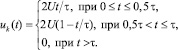
Здесь U = 10^–6 м3, τ = 2 c.

Система обыкновенных дифференциальных уравнений (7), (4) 12-го порядка решалась численно методом Рунге – Кутты с постоянным временным шагом Δt = 0,05 с. Размер шага интегрирования выбирался в ходе численных экспериментов.

Результаты численного решения представлены на рис. 3–4. На рис. 3 показаны изменения обобщенных координат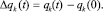

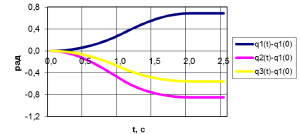
Рис. 3. Графики изменения обобщенных координат механизма

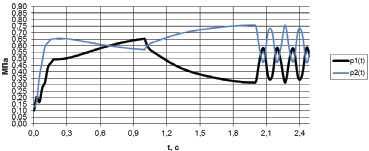
Рис. 4. Изменение давлений в полостях двигателя G1

На рис. 4 показаны изменения давлений рабочей жидкости в полостях двигателя G1; черного цвета кривые соответствуют рабочей, а синяя – сливной полости. Наблюдаемые колебания объясняются сжимаемостью рабочей жидкости.

Заключение

Представленная математическая модель дает единообразное описание кинематики и динамики гидропривода вращательного звена механизма при произвольном расположении гидродвигателя поступательного действия. Векторные формы представления обобщенных сил (2) и передаточных функций (6) удобны для использования в алгоритмах автоматического формирования уравнений динамики механизма.

Работа выполнена в рамках ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014–2020 годы» Минобрнауки России.

Рецензенты:

Полянин И.А., д.т.н., профессор кафедры транспортных и технологических машин, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;

Сидыганов Ю.Н., д.т.н., профессор кафедры эксплуатации машин и оборудования, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.

Работа поступила в редакцию 15.05.2014.

Библиографическая ссылка