В процессе эксплуатации приборов с парами натрия натрий диффундирует в оксидное покрытие катода, что приводит к снижению его работы выхода и увеличению коэффициента ионно-электронной эмиссии [5]. Дальнейшее улучшение характеристик приборов с парами натрия требует проведения исследований влияния натрия на параметры оксидного катода (ОК). Однако экспериментальное исследование процессов, происходящих в ОК при воздействии натрия, осложняется высокой химической активностью натрия, что ограничивает применение традиционных методов исследований. В этом плане компьютерное моделирование позволяет учесть процессы, протекающие в покрытии катода при адсорбции натрия, а также снизить материальные затраты на проведение экспериментов.
Ниже рассматривается расчет коэффициента диффузии натрия в бариевый катод.
Физическая модель диффузии натрия в оксидном покрытии
Структура кристалла оксида бария после термовакуумной обработки представляет собой гранецентрированный куб, в узлах кристаллической решетки располагаются атомы бария и кислорода (рис. 1) [1]. В целях упрощения модели кристалла оксида бария рассмотрим линейный случай кубической решетки с восьмью узлами (рис. 2).
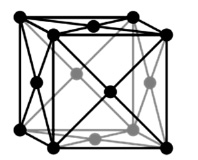
Рис. 1. Гранецентрированный куб
При сближении атомов в направлении друг к другу возможно появление вакансии. Объем вакансии в гранецентрированном кристалле составляет приблизительно 0,5–0,6 от объема атома, следовательно, вероятность образования вакансии для двухмерного случая составляет около 25 % [1].
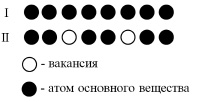
Рис. 2. Вероятное распределение вакансий в одномерном случае
Коэффициент диффузии D определяется [2]:
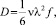 (1)
(1)
где v – частота перескоков атомов; λ – длина диффузионного скачка, соответствующая межатомному расстоянию; f – корреляционный множитель.
Как известно, процесс диффузии можно рассматривать как серию последовательных перескоков атомов с их узлов в вакансии. В этом плане нами рассмотрен как наиболее вероятный вакансионный механизм диффузии. Частота перескоков атома v определяется в виде:
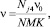 (2)
(2)
где Nj4 – количество диффузионных скачков меченого атома натрия, получаемое по окончанию работы программы; v0 – частота, соответствующая частоте колебаний узлов кристаллической решетки; NMK – количество машинных циклов Монте-Карло.
Вероятность диффузионного скачка, необходимая для имитации случайных перемещений атома натрия в кристалле, определяется [2]:
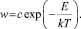 (3)
(3)
Здесь с – поправочный коэффициент; E – энергия активации диффузии; k – постоянная Больцмана; Т – температура кристалла.
При рассмотрении диффузии предполагается, что вероятность атомных скачков не зависит от направлений предшествующих перемещений. Однако в реальных кристаллах существует зависимость вероятности диффузионного скачка от предшествующих перемещений атома. Каждый диффузионный скачок связан с предыдущим, и атом совершает не случайные, а коррелированные блуждания, что учитывает f корреляционный множитель [3]:
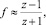 (4)
(4)
где z – число ближайших соседей атома. Корреляционный множитель показывает долю скачков, вносящих эффективный вклад в диффузию.
Подставляя (2), (4) в (1), получаем:
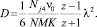 (5)
(5)
Используя формулу (5), можно рассчитать коэффициент диффузии натрия в оксиде бария.
Компьютерная программа расчета коэффициента диффузии
Компьютерная программа расчета коэффициента диффузии натрия в оксид бария разработана нами на языке программирования С++ (рис. 3).
В основе модели использован двухмерный массив размерности 100×30 ячеек кристалла оксида бария. Края массива были замкнуты с помощью периодических граничных условий. Элементы целочисленного массива представляли собой атомы взаимодействующих атомов и вакансии (рис. 4, а). Атомы задавались трех сортов: 1 – атом бария, 3 – атом натрия, 0 – вакансия, 4 – меченый атом натрия.
В рассматриваемом случае диффузия натрия осуществлялась из постоянного источника. Для этого выбиралось определенное количество NMK циклов Монте-Карло, и происходил перебор атомов в массиве на возможность совершить диффузионный скачок. Вероятность диффузионного скачка натрия или вакансии определялась по формуле (3). Она сравнивалась со значением числа, полученного с помощью генератора случайных чисел. Вероятность диффузионного скачка, как известно, зависит от энергии активации диффузии. Она имеет различные значения для разных сортов атомов. Так, если:
1. Выпадал элемент массива, равный «3», то возможен однонаправленный акт диффузии.
2. Выпадал элемент массива, равный «0» или «1», то возможен акт обмена.
В этом случае движение вакансий по кристаллу происходило в двух направлениях.
После реализации одного из указанных событий поверхностный слой оксида бария пополнялся слоем натрия. На этом цикл счета являлся завершенным. После чего следовал новый цикл счета, в котором происходили аналогичные события.
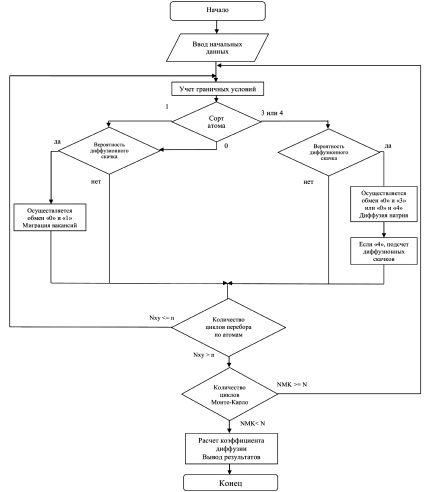
Рис. 3. Блок-схема расчета коэффициента диффузии натрия в оксиде бария
В результате счета определено число скачков меченого атома, а также всех атомов натрия в оксиде бария. Коэффициент диффузии рассчитывался по формуле (5).
Расчет коэффициента диффузии натрия в оксиде бария осуществлялся при следующих параметрах: T = 600 K, энергии активации диффузии Е натрия и вакансий соответственно равны 0,5 и 0,3 эВ [4], λ = 2,77 А [4], τ0 = 10–13 с и v = 1013 [1], z = 2 [2], количество NMK выбрано нами 4∙106.
В результате работы программы мы получили значение коэффициента диффузии натрия, суммарное количество скачков и количество скачков меченого атома натрия, а также распределение атомов в кристалле (рис. 4, б).
Из рис. 4, б следует, что с течением времени происходит насыщение кристалла оксида бария натрием. Расчетное значение коэффициента диффузии в оксид бария при температуре 600 К составляет D = 1,47∙10–12 м2/с, что достаточно близко к экспериментальному значению D = 1,2∙10–12 м2/с, приведённому в работе [6]. Результаты компьютерного моделирования дополнительно подтверждают вакансионный механизм диффузии натрия в оксиде бария.
 а
а  б
б
Рис. 4. Распределение атомов в кристалле оксида бария: а – в начале работы программы; б – по истечении работы программы
Предложенный нами метод расчета коэффициента диффузии натрия в оксиде бария после некоторых уточнений может быть распространен и для оксидных покрытий, имеющих сложный элементный состав.
Рецензенты:
Кузьмичев Н.Д., д.ф.-м.н., профессор, заведующий кафедрой общенаучных дисциплин, ФГБОУ ВПО «Мордовский государственный университет имени Н.П. Огарева», г. Саранск;
Малыханов Ю.Б., д.ф.-м.н., профессор, ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.
Работа поступила в редакцию 26.03.2014.
Библиографическая ссылка
Свешников В.К., Базаркин А.Ф. ФИЗИЧЕСКАЯ МОДЕЛЬ И КОМПЬЮТЕРНЫЙ РАСЧЕТ КОЭФФИЦИЕНТА ДИФФУЗИИ НАТРИЯ В ОКСИДНОЕ ПОКРЫТИЕ КАТОДА // Фундаментальные исследования. 2014. № 5-5. С. 990-993;URL: https://fundamental-research.ru/ru/article/view?id=34031 (дата обращения: 28.02.2026).



