Для решения задач многокритериальной оптимизации и принятия решений в задачах многокритериального выбора применяются различные механизмы комплексного оценивания, предназначенные для агрегирования разнородной информации об объектах сопоставления в единый комплексный (интегральный) показатель. Наличие комплексного показателя позволяет ранжировать любые объекты на всей области определения характеристик, описывающих данные объекты, и определять степень преимущества (недостатка) некоторого объекта перед другими. Это обстоятельство делает возможными описания процедуры выбора (принятия решения) субъекта и обоснования субъектно-оптимальных решений в задачах управления.
Для комплексного оценивания объектов различной природы, описываемых набором характеристик, являющихся по отношению друг к другу гетерогенными, могут использоваться взвешенные уравнения, к которым относятся квалиметрические модели (см., например [6]) модели, предлагаемые в теории важности критериев (см., например [12]). Адекватность данных методов в первую очередь зависит от корректности выбора взвешенных коэффициентов, определяющих важность отдельных критериев. Обзор методов определения коэффициентов важности приводится в работе [3].
В качестве альтернативного подхода к комплексному оцениванию может выступить известный в теории активных систем [4] механизм комплексного оценивания, основанный на деревьях целей (критериев) и бинарных матриц свертки частных критериев. В работе [15] описаны функциональные возможности, которые появляются у матричных механизмов комплексного оценивания, основанных на процедуре нечеткого комплексного оценивания. Матричная процедура нечеткого комплексного оценивания впервые была предложена в работе [2]. Развитие механизмов нечеткого комплексного оценивания описано в работе [1].
Матричные механизмы комплексного оценивания получили широкое распространение в российской литературе [1, 2, 9, 13–15] и практике комплексного оценивания. По этой причине в анализе последних исследований и публикаций представлены преимущественно работы российских ученых, опубликованные на русском языке.
Несмотря на то, что на базе процедуры нечеткого комплексного оценивания, которая будет описана ниже, уже создан ряд программных продуктов класса ДЕКОН (см., например, [13]), изначально предназначавшихся для оценивания объектов недвижимости, из-за чего и было придумано их общее название, сокращено от «Дерево Комплексного Оценивания Недвижимости», данные технологии все же не получили широкого распространения в практике, что и определило цель данной статьи. Следует отметить, что сокращенное название класса программных продуктов сохранило привязку к объектам недвижимости, но все они реализованы как универсальные вычислительные комплексы, где могут оцениваться объекты самой различной природы.
Главной целью данной статьи является разработка алгоритмов процедуры нечеткого комплексного оценивания, доступных для реализации даже на базе электронных таблиц, входящих в состав стандартных офисных программ, например, MS Excel, что в конечном счете позволит сделать данную технологию комплексного оценивания более доступной для исследователей, занимающихся проблемами многокритериальной оптимизации и принятия решений в задачах многокритериального выбора.
Комплексное оценивание осуществляется посредством последовательной свертки аргументов, соответствующих характеристикам, описывающим объект оценивания.
Свертку пары аргументов можно представить в виде матрицы M размерностью m×m, где m – максимальное значение шкалы комплексного оценивания. Для комплексного оценивания, используя матричные свертки, целесообразно использовать шкалу оценивания Х = {1, 2, 3, 4}, что делает размерность матрицы M – 4×4 (рис. 1). Далее при описании алгоритмов процедуры нечеткого комплексного оценивания и самой процедуры будем полагать, что используется именно эта шкала, хотя в некоторых работах, например [5], используется шкала {1, 2, 3}, в других, например [11] – {1, 2, 3, 4, 5}. Эффективность четырехбалльной шкалы описан в работах [9, 14].

Рис. 1. Матрица свертки размерностью 4×4, образованная шкалами оценивания аргументов свертки
Элементы матрицы свертки mij заполнятся экспертно, где i и j номера строк и столбцов матрицы (см. рис. 1), соответственно. В общем случае элементы m11 и m44 полагаются инвариантными и равными 1 и 4, соответственно, так как при наихудшем состоянии сворачиваемых аргументов (Хi = Хj = 1) можно полагать, что свертка также будет описываться наихудшей оценкой (m11 = 1), во втором случае (Хi = Хj = 4) наилучшей (m44 = 4).
В общем случае аргумент свертки и элементы матрицы M могут быть заданы экспертом (группой экспертов) как дискретными значениями шкалы, что соответствует тому, что объект однозначно интерпретируется, а составные правила вывода в матрице формализуются в виде категорических суждений [7], так и значениями непрерывной шкалы, что соответствует модальным суждениям [7], которые можно формализовать, используя теорию нечетких множеств [8].
Под нечетким множеством понимается совокупность пар Х/μХ, в данном случае состоящих из дискретных значений оценок используемой шкалы Х = {1, 2, 3, 4} и значений функции принадлежности μХ (рис. 2), под которыми можно понимать степень уверенности эксперта в том, что оцениваемый объект описывается оценкой Х с соответствующей ей интерпретацией.
Если каждый аргумент свертки представить в виде нечетких множеств, то матрица свертки М может быть также представлена в виде нечеткого множества (рис. 3).
Для определения одного значения функции принадлежности, соответствующей элементу матрицы, необходимо использовать теоретико-множественную операцию пересечения, в соответствии с принципом обобщения Заде [8], который в общем случае для двух произвольных нечетких множеств  и
и 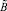 записывается следующим образом (1):
записывается следующим образом (1):
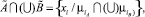 (1)
(1)
где xi – элемент носителей нечетких множеств  и
и 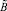 ,
, 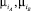 значения функций принадлежности элемента xi нечеткому множеству
значения функций принадлежности элемента xi нечеткому множеству  и
и 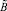 , соответственно,
, соответственно, 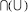 – операция пересечения (объединения). Согласно процедуре нечеткого комплексного оценивания теоретико-множественную операцию объединения необходимо выполнять для элементов матрицы свертки, имеющих одинаковые значения, которые образуют носитель свертки в нечетком виде.
– операция пересечения (объединения). Согласно процедуре нечеткого комплексного оценивания теоретико-множественную операцию объединения необходимо выполнять для элементов матрицы свертки, имеющих одинаковые значения, которые образуют носитель свертки в нечетком виде.
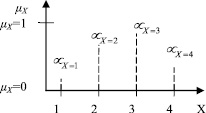
Рис. 2. Модель представления аргумента свертки или свертки в виде нечеткого множества

Рис. 3. Матрица свертки M, где аргументы свертки и элементы матрицы представлены в виде нечетких множеств
Алгоритм операции пересечения нечетких множеств в процедуре нечеткого комплексного оценивания представлен на рис. 4. Алгоритм операции объединения нечетких множеств в процедуре нечеткого комплексного оценивания представлен на рис. 5.
Существует два традиционных подхода к теоретико-множественным операциям объединения и пересечения над нечеткими множествами: максиминный (2)–(3) и вероятностный (4)–(5) подходы, которые сам Л. Заде называл «жесткими» и «мягкими» [8] соответственно и не исключал возможности применения любого из них:
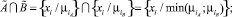 (2)
(2)
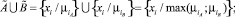 (3)
(3)
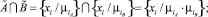 (4)
(4)
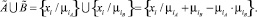 (5)
(5)
Следует отметить, что по аналогии с теорией вероятностей [10], в случае несвязных событий, вероятность наступления которых определяется простой суммой вероятностей этих событий, можно сформулировать еще один подход к теоретико-множественной операции объединения нечетких множеств:
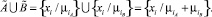 (6)
(6)
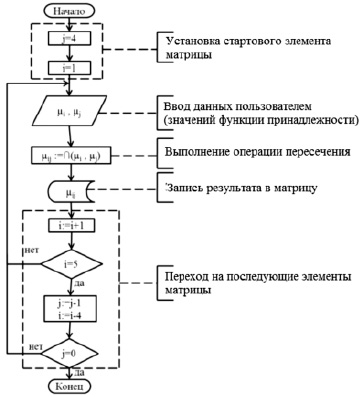
Рис. 4. Алгоритм операции пересечения нечетких множеств в процедуре нечеткого комплексного оценивания
После выполнения нечеткого комплексного оценивания, используя любой подход к теоретико-множественным операциям, свертка будет представлять собой не матрицу в нечетком виде, а обычное нечеткое множество, носителем которого будет шкала комплексного оценивания. Для представления результата свертки в виде числа, принадлежащего множеству действительных чисел, в работах [9, 14, 15] предлагается использовать уравнение центра тяжести:
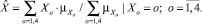 (7)
(7)
Авторами доказано, что, используя в процедуре нечеткого комплексного оценивания операцию пересечения (4) и объединения (6) (авторами данный подход предлагается называть аддитивно-мультипликативным), удается матричную свертку на непрерывной области определения аргументов сделать монотонной и гладкой для стандартных функций свертки и кусочно-гладкой на всем множестве определения аргументов свертки, что позволяет расширить применяемый набор инструментов исследования в задачах принятия многокритериальных решений и многокритериальной оптимизации.
В связи с вышесказанным авторы рекомендуют при создании прикладных программных комплексов использовать аддитивно-мультипликативный подход к теоретико-множественным операциям пересечения и объединения нечетких множеств, так как такой подход не обладает погрешностями процедуры нечеткого комплексного оценивания или реализовать все подходы (2)–(6) с возможностью их выбора.
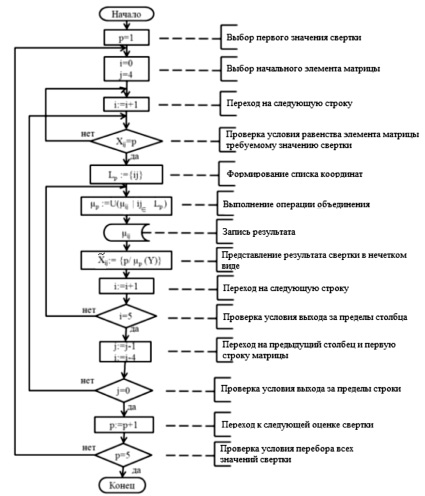
Рис. 5. Алгоритм операции объединения нечетких множеств в процедуре нечеткого комплексного оценивания
Статья подготовлена при финансовой поддержке Пермского национального исследовательского политехнического университета.
Рецензенты:
Столбов В.Ю., д.т.н., профессор, декан факультета прикладной математики и механики, Пермский национальный исследовательский политехнический университет, г. Пермь;
Федосеев С.А., д.т.н., доцент, генеральный директор ЗАО «Геликон Про», г. Пермь.
Работа поступила в редакцию 18.02.2014.
Библиографическая ссылка
Алексеев А.О., Калентьева А.С., Вычегжанин А.В., Климец Д.В. АЛГОРИТМИЧЕСКИЕ ОСНОВЫ НЕЧЕТКОЙ ПРОЦЕДУРЫ КОМПЛЕКСНОГО ОЦЕНИВАНИЯ ОБЪЕКТОВ РАЗЛИЧНОЙ ПРИРОДЫ // Фундаментальные исследования. 2014. № 3-3. С. 469-474;URL: https://fundamental-research.ru/ru/article/view?id=33697 (дата обращения: 16.02.2026).



