Термическое взаимодействие высокотемпературного расплавленного топлива с охладителем может иметь место в реакторах с натриевым теплоносителем при реактивностных авариях с быстрым ростом мощности и при авариях с нарушением охлаждения активной зоны (аварии типа ULOF). Происходящее при этом взаимодействии высвобождение большого количества механической энергии представляет собой угрозу для безопасности АЭС и в связи с этим данное явление является предметом многочисленных исследований [5, 6, 12]. В настоящей работе предложена математическая модель, позволяющая оценивать параметры термического взаимодействия расплава с жидким натрием. Эта модель была валидирована на опытных данных, полученных на установке THINA (Германия), где расплав подавался в нижнюю часть экспериментального сосуда с натрием, и на установке FARO (Италия), где расплав подавался сверху (рис. 1). Было получено хорошее совпадение расчётных и экспериментальных данных как по давлению в зоне взаимодействия, так и по коэффициентам конверсии.
Цель работы: разработка и валидация модели термического взаимодействия расплава с натриевым теплоносителем.
Материал и методы исследования
Основные предположения при разработке математической модели заключаются в следующем. Процесс взаимодействия расплава с натрием разделяется на две временные фазы. На первой фазе расплав материалов активной зоны мгновенно превращается в мелкие частицы и вступает в непосредственный контакт с жидким натрием. Процесс теплопередачи характеризуется:
1) интенсивным тепловым взаимодействием между расплавом и охладителем за счёт прямого контакта между ними;
2) большой площадью поверхности взаимодействия, обусловленной малым размером частиц.
По мере охлаждения частиц расплава скорость теплопередачи в жидкий натрий снижается. Расчёт температуры частиц основан на решении нестационарного уравнения теплопроводности, записанного для сферически симметричного случая, с граничным условием третьего рода.
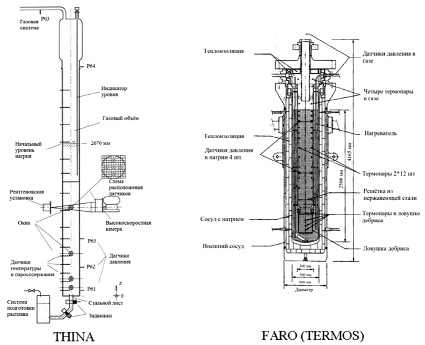
Рис. 1. Экспериментальные установки THINA и FARO
Нагреваемый объём натрия в зоне взаимодействия ограничен окружающим холодным теплоносителем и другими материалами, присутствующими в активной зоне. Для описания быстрого расширения нагреваемого объёма натрия в предлагаемой математической модели на начальном этапе используется уравнение движения, записанное в акустическом приближении, а затем движение столба натрия определяется силами, действующими на него.
Вторая фаза процесса термического взаимодействия начинается с момента закипания натрия. С этого момента теплопередача характеризуется:
1) ухудшением теплопередачи между расплавом и охладителем из-за образования плёнки пара натрия на внешней поверхности фрагментов расплава;
2) большой площадью поверхности взаимодействия.
Для описания процессов, имеющих место на первой и второй фазах процесса, формулируются уравнения сохранения массы и энергии для зоны термического взаимодействия и уравнение импульса для движущегося столба холодного натрия.
Описанная модель основана на [1, 4, 11]. Дополнительно к этим исследованиям в настоящей работе для расчёта теплообмена частиц расплава при плёночном кипении были использованы зависимости [2, 4, 7, 9]. Стоит отметить, что в моделируемых экспериментах газовая полость над уровнем натрия была заполнена аргоном. Для учёта процессов в газовой полости математическая модель была дополнена уравнениями сохранения массы и энергии для аргона и уравнением теплообмена газа со стенками сосуда. Подробное описание математической модели изложено в [3].
Результаты исследования и их обсуждение
Расчёт эксперимента THINA
Установка THINA (см. рис. 1) состоит из двух основных частей: экспериментального сосуда и системы для приготовления и инжекции расплава. Около половины экспериментального сосуда заполнено жидким натрием, над поверхностью которого находится газ (аргон) для компенсации объёмных расширений. Малый диаметр сосуда (0,3 м) был выбран для возможности использования рентгеновского излучения с целью диагностики исследуемых процессов. Около 5 кг расплава подготавливалось в тигле с помощью экзотермической реакции алюминий/оксид железа согласно уравнению:
2Al + Fe2O3 = 2Fe + Al2O3 + 4117 Дж/г.
Продукты реакции разделяются в ходе и после реакции за счёт разности их плотностей. Этот эффект был учтён в конструкции тиглей, один из которых позволяет подавать расплав, состоящий главным образом из алюминия, а второй – в большей части из железа.
Предложенная модель была валидирована на всех четырёх экспериментах [10]. В данной работе приводятся результаты расчётов эксперимента TH561, основные параметры которого приведены в таблице:
Основные параметры экспериментов
|
TH 561 (THINA) |
T2 (FARO) |
|
|
Температура расплава, К |
2780 |
3273 |
|
Время подачи расплава, с |
0,190 |
- |
|
Состав расплава |
4 кг Al2O3 + 1,5 кг стали |
112 кг UO2 + 28кг ZrO2 |
|
Масса натрия, кг |
155 |
130 |
|
Температура натрия, К |
790 |
673 |
|
Высота столба натрия, м |
2,67 |
2,5 |
|
Начальное давление аргона, бар |
1,1 |
1,3 |
С помощью разработанной математической модели были получены следующие результаты. Рассчитанный пик давления в зоне взаимодействия составил 7,4 бар, что хорошо согласуется с экспериментально полученным значением в 8,0 бар. Временные зависимости основных параметров, полученных в эксперименте и в расчёте, приведены на рис. 2. Коэффициент конверсии, полученный в эксперименте для данного теста, составил 0,13 %, что несколько выше полученного значения с помощью разработанной математической модели – 0,07 %. На рис. 2, 3 наблюдается качественное соответствие расчётных и экспериментальных данных. Различия вызваны принятой схематизацией исследуемого процесса (интегральный подход для формулировки законов сохранения) и неполнотой информации о параметрах экспериментальной установки и теплофизических свойств высокотемпературного расплава. Расчёты трёх других экспериментов на установке THINA [10] дали аналогичные результаты.
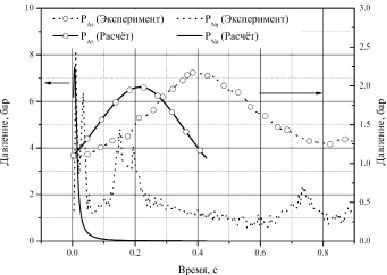
Рис. 2. Временные зависимости давления натрия в зоне взаимодействия, давления аргона
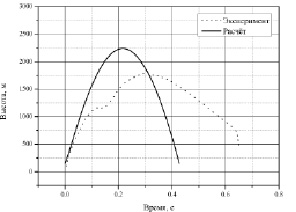
Рис. 3. Временная зависимость высоты зоны взаимодействия
Расчёт эксперимента FARO
Установка FARO [10] состоит из экспериментального сосуда TERMOS и системы подачи кориума.
TERMOS представляет собой сосуд высокого давления, внешним диаметром 800 мм и высотой 4,0 м. Контейнер с натрием находится внутри сосуда TERMOS и имеет диаметр 470 мм. Экспериментальный сосуд подсоединен к устройству для подготовки расплава через канал и три межсекционных клапана. Объём инертного газа, находящегося над уровнем натрия, составлял 0,15 м3. Температура натрия равна 673,15 К, уровень жидкого натрия – 2,5 м. Начальные условия эксперимента приведены в таблице.
Основным параметром, используемым для валидации модели на этом эксперименте, является максимальный пик давления в зоне взаимодействия. Рассчитанное значение в зоне взаимодействия составило 82 бар, что хорошо согласуется с экспериментально полученным значением в 80 бар.
Выводы
Предложена модель термического взаимодействия расплава с натрием, основанная на законах сохранения массы и энергии для зоны взаимодействия и импульса для столба холодного натрия. Данная модель была валидирована для двух типов взаимодействия: при подаче расплава в нижнюю часть экспериментального сосуда (THINA) и в верхнюю (FARO). Сравнение проводилось по нескольким параметрам: максимальное давление в натрии и аргоне, высоты подъёма столба натрия и коэффициентов конверсии. Было получено приемлемое соответствие расчётных и экспериментальных результатов.
Работа была выполнена при финансировании ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг. (госконтракт № 14.В37.21.0151), НИР НИУ«МЭИ» «Исследование теплофизических процессов в перспективном энергетическом оборудовании» рег. № 7.3163.2011, проекта РФФИ № 11-08-00410_а.
Рецензенты:
Семенов В.Н., д.ф.-м.н., заведующий отделом моделирования АЭС с реакторными установками нового поколения, ФГБУН «Институт проблем безопасного развития атомной энергии» РАН, г. Москва;
Якуш С.Е., д.ф.-м.н., ведущий научный сотрудник лаборатории термогазодинамики и горения, ФГБУН «Институт проблем механики им. А.Ю. Ишлинского» РАН, г. Москва.
Работа поступила в редакцию 12.03.2013.
Библиографическая ссылка
Мелихов В.И., Мелихов О.И., Парфенов Ю.В., Ртищев Н.А., Тарасов А.Е. РАЗРАБОТКА И ВАЛИДАЦИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ОЦЕНКИ ПАРАМЕТРОВ ТЕРМИЧЕСКОГО ВЗАИМОДЕЙСТВИЯ РАСПЛАВА С НАТРИЕВЫМ ТЕПЛОНОСИТЕЛЕМ // Фундаментальные исследования. 2013. № 4-5. С. 1079-1083;URL: https://fundamental-research.ru/ru/article/view?id=31364 (дата обращения: 03.03.2026).



